3.8: Angles and Perpendicular Lines
- Page ID
- 4770
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lines that intersect at a 90 degree or right angle.
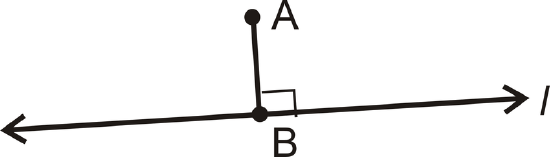
Two lines are perpendicular when they intersect to form a \(90^{\circ}\) angle. Below, \(l\perp \overline{AB}\).
In the definition of perpendicular the word “line” is used. However, line segments, rays and planes can also be perpendicular. The image below shows two parallel planes, with a third blue plane that is perpendicular to both of them.

Basic Facts about Perpendicular Lines
Theorem #1: If \(l\parallel m\) and \(n\perp l\), then \(n\perp m\).
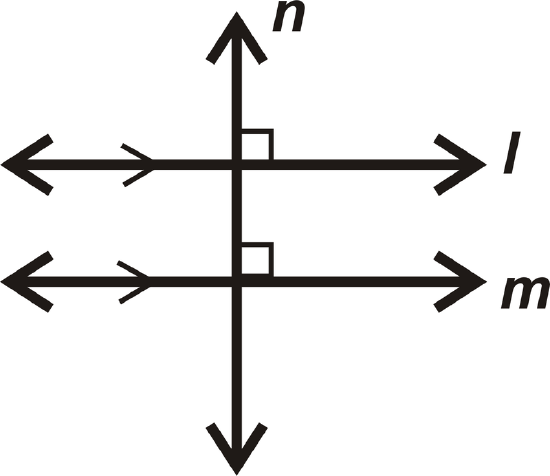
Theorem #2: If \(l\perp n\) and \(n\perp m\), then \(l\parallel m\).

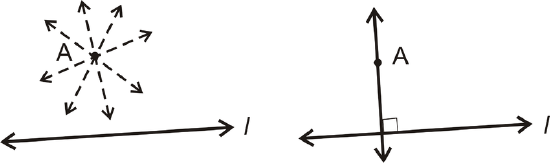
Postulate: For any line and a point not on the line, there is one line perpendicular to this line passing through the point. There are infinitely many lines that pass through \(A\), but only one that is perpendicular to \(l\).
What if you were given a pair of lines that intersect each other at a \(90^{\circ}\) angle? What terminology would you use to describe such lines?
Example \(\PageIndex{1}\)
Determine the measure of \(\angle 1\).
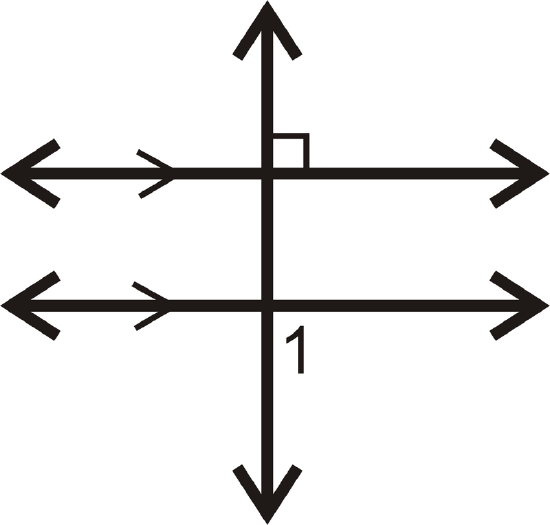
Solution
We know that both parallel lines are perpendicular to the transversal.
\(m\angle 1=90^{\circ}\).
Example \(\PageIndex{2}\)
Find \(m\angle 1\).
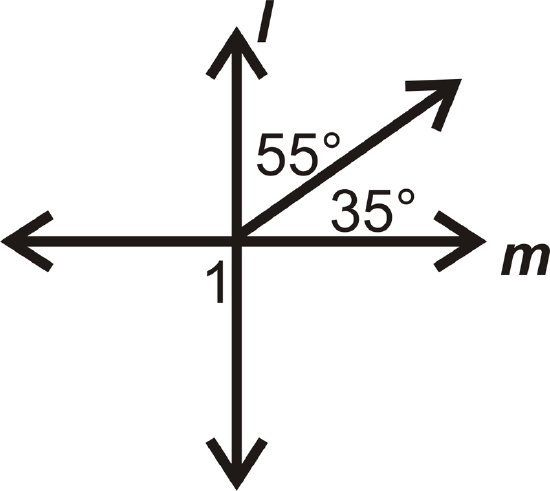
Solution
The two adjacent angles add up to \(90^{\circ}\), so \(l\perp m\).
\(m\angle 1=90^{\circ}\)
because it is a vertical angle to the pair of adjacent angles and vertical angles are congruent.
Example \(\PageIndex{3}\)
Which of the following is the best example of perpendicular lines: Latitude on a Globe, Opposite Sides of a Picture Frame, Fence Posts, or Adjacent Sides of a Picture Frame?
Solution
The best example would be adjacent sides of a picture frame. Remember that adjacent means next to and sharing a vertex. The adjacent sides of a picture frame meet at a \(90^{\circ}\) angle and so these sides are perpendicular.
Example \(\PageIndex{4}\)
Is \(\overleftrightarrow{SO} \perp \overrightarrow{GD}\)?
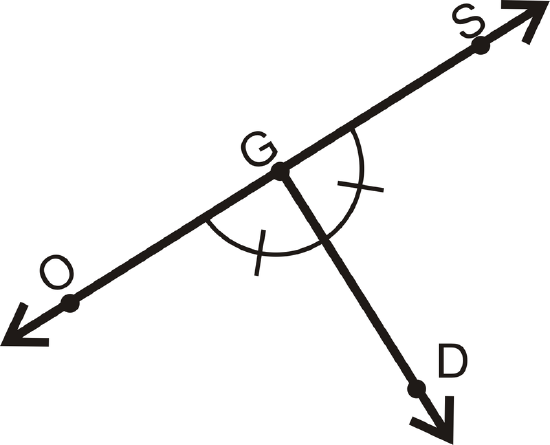
Solution
\(\angle OGD\cong \angle SGD\) and the angles form a linear pair. This means both angles are \(90^{\circ}\), so the lines are perpendicular.
Example \(\PageIndex{5}\)
Write a 2-column proof to prove Theorem #1. Note: You need to understand corresponding angles in order to understand this proof. If you have not yet learned corresponding angles, be sure to check out that concept first, or skip this example for now.
Given: \(l\parallel m\), \(l\perp n\)
Prove: \(n\perp m\)
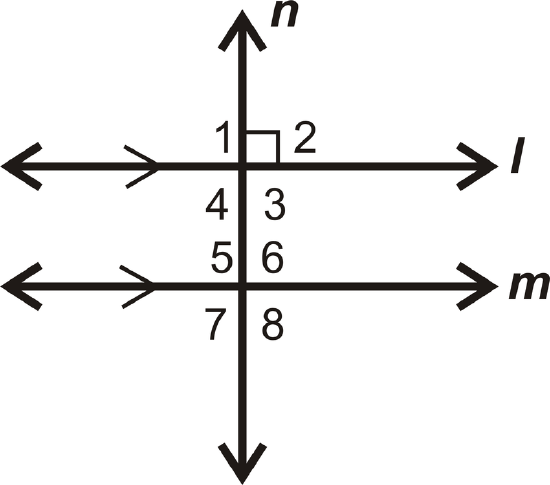
Solution
| Statement | Reason |
|---|---|
| 1. \(l\parallel m\), \(l\perp n\) | 1. Given |
| 2. \(\angle 1\), \(\angle 2\), \(\angle 3\), and \(\angle 4 are right angles\) | 2. Definition of perpendicular lines |
| 3. \(m\angle 1=90^{\circ}\) | 3. Definition of a right angle |
| 4. \(m\angle 1=m\angle 5\) | 4. Corresponding Angles Postulate |
| 5. \(m\angle 5=90^{\circ}\) | 5. Transitive \(PoE\) |
| 6. \(m\angle 6=m\angle 7=90^{\circ}\) | 6. Congruent Linear Pairs |
| 7. \(m\angle 8=\(90^{\circ}\) | 7. Vertical Angles Theorem |
| 8. \(\angle 5\), \(\angle 6\), \(\angle 7\), and \(\angle 8\) are right angles | 8. Definition of right angle |
| 9. \(n\perp m\) | 9. Definition of perpendicular lines |
Review
Use the figure below to answer questions 1-2. The two pentagons are parallel and all of the rectangular sides are perpendicular to both of them.

- List a pair of perpendicular lines.
- For \(\overline{AB}\), how many perpendicular lines would pass through point \(V\)? Name this/these line(s).
Use the picture below for question 3.
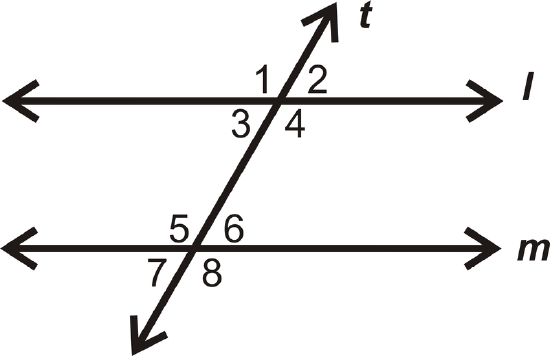
- If \(t\perp l\), is \(t\perp m\)? Why or why not?
Find the measure of \(\angle 1\) for each problem below.
-
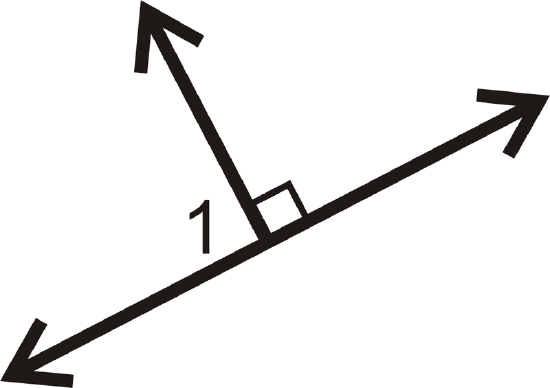
Figure \(\PageIndex{12}\) -
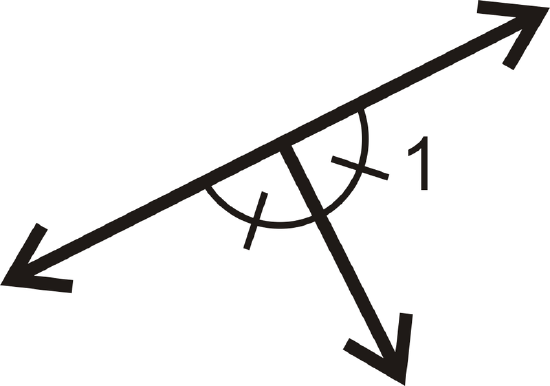
Figure \(\PageIndex{13}\) -
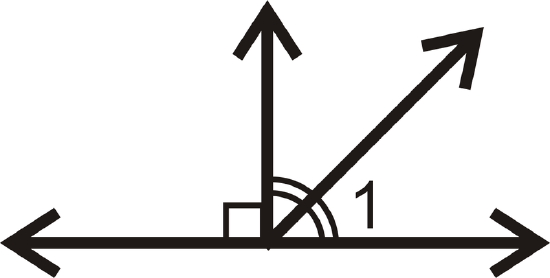
Figure \(\PageIndex{14}\) -
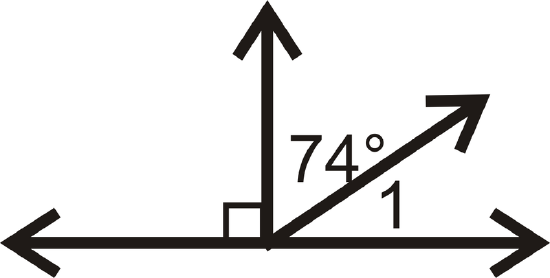
Figure \(\PageIndex{15}\) -
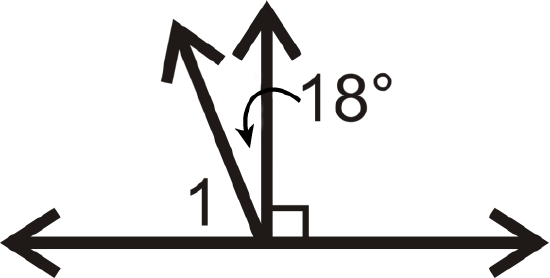
Figure \(\PageIndex{16}\) -
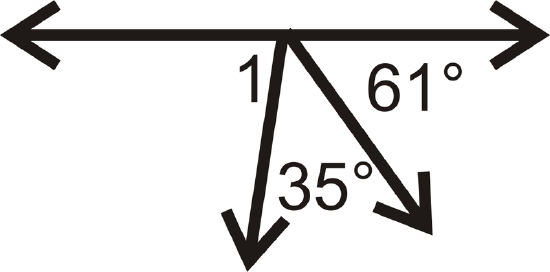
Figure \(\PageIndex{17}\) -
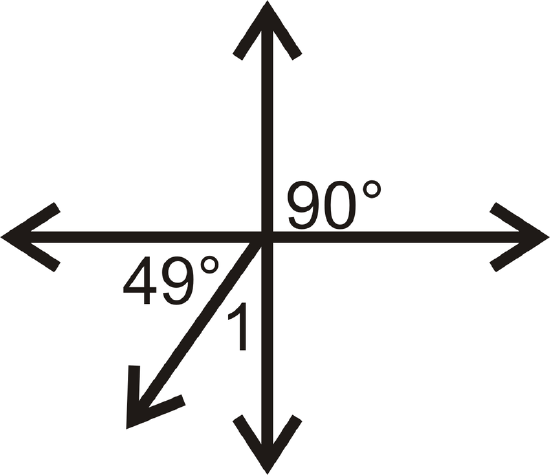
Figure \(\PageIndex{18}\) -
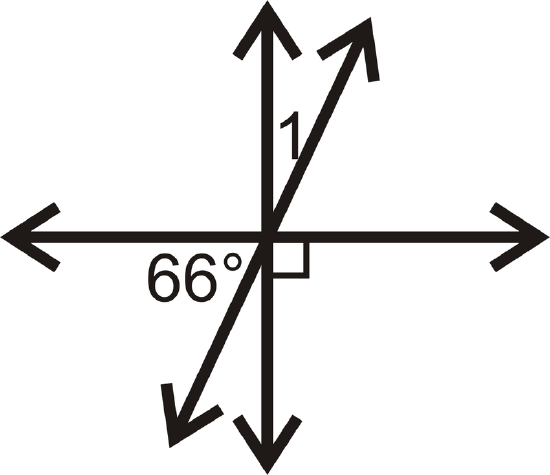
Figure \(\PageIndex{19}\) -
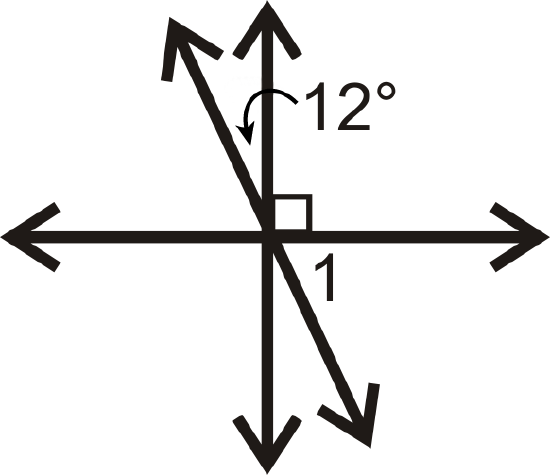
Figure \(\PageIndex{20}\)
In questions 13-16, determine if \(l\perp m.\)
-
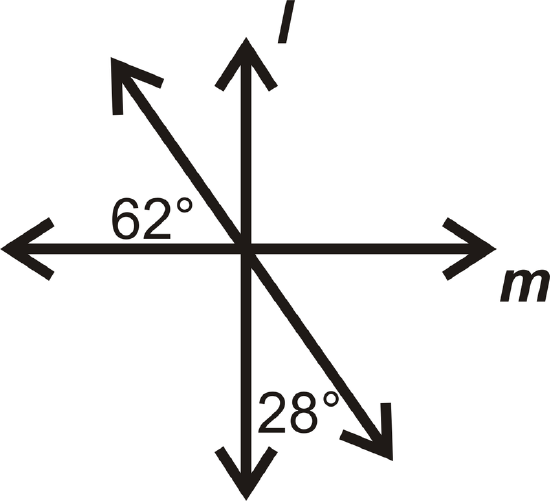
Figure \(\PageIndex{21}\) -
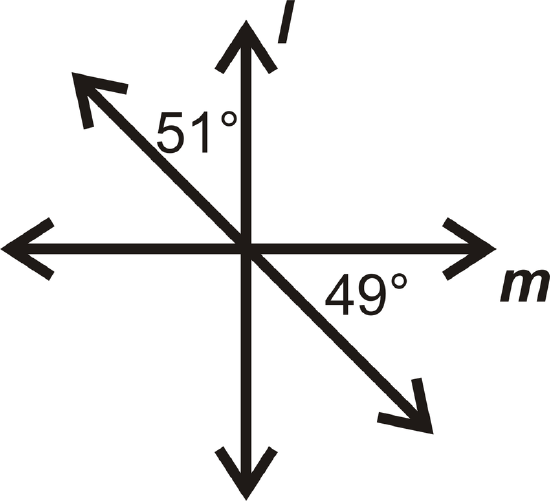
Figure \(\PageIndex{22}\) -
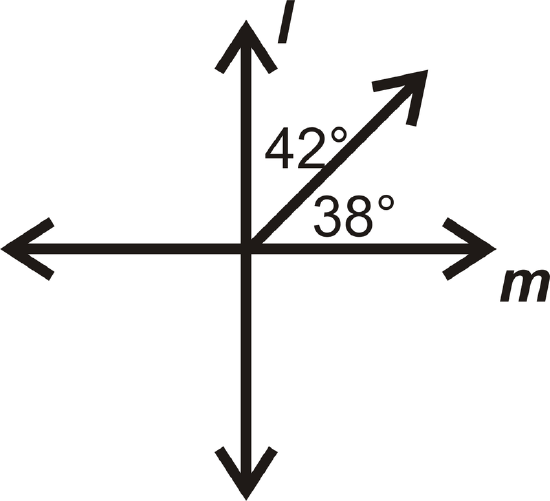
Figure \(\PageIndex{23}\) -
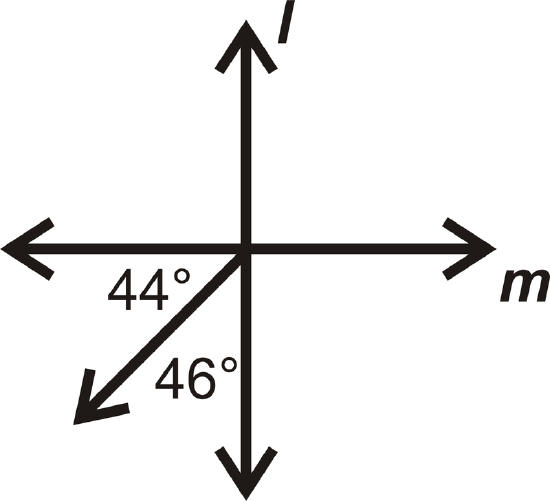
Figure \(\PageIndex{24}\)
Fill in the blanks in the proof below.
- Given: \(l\perp m\), \(l\perp n\) Prove: \(m\parallel n\)
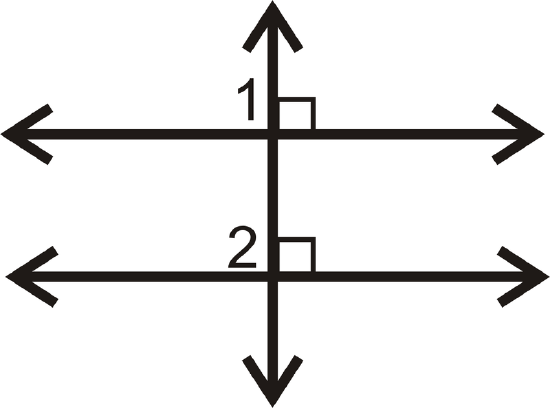
| Statement | Reason |
|---|---|
| 1. | 1. |
| 2. \(\angle 1\) and \(\angle 2\) are right angles | 2. |
| 3. | 3. Definition of right angles |
| 4. | 4. Transitive \(PoE\) |
| 5. \(m\parallel n\) | 5. |
Resources
Vocabulary
| Term | Definition |
|---|---|
| perpendicular | Two lines are perpendicular when they intersect to form a \(90^{\circ}\) angle. |
| Angle | A geometric figure formed by two rays that connect at a single point or vertex. |
| Perpendicular lines | Perpendicular lines are lines that intersect at a \(90^{\circ}\) angle. |
Additional Resources
Interactive Element
Video: Perpendicular Lines Principles - Basic
Activities: Perpendicular Lines Discussion Questions
Study Aids: Lines and Angles Study Guide
Practice: Angles and Perpendicular Lines
Real World: Turning The Tables

