3.2: Parallel and Skew Lines
- Page ID
- 2189
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lines that never intersect.
Parallel lines are two or more lines that lie in the same plane and never intersect. To show that lines are parallel, arrows are used.
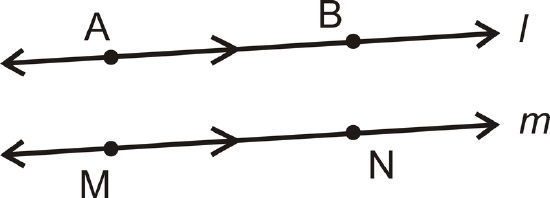
| Label It | Say It |
|---|---|
| \(\overleftrightarrow{AB} \parallel \overleftrightarrow{MN}\) | Line \(AB\) is parallel to line \(MN\) |
| \(l\parallel m\) | Line \(l\) is parallel to line \(m\). |
In the definition of parallel the word “line” is used. However, line segments, rays and planes can also be parallel. The image below shows two parallel planes, with a third blue plane that is perpendicular to both of them.
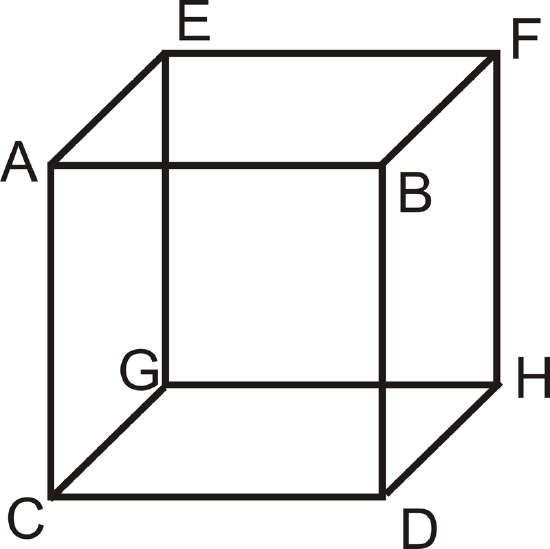
Skew lines are lines that are in different planes and never intersect. They are different from parallel lines because parallel lines lie in the SAME plane. In the cube below, \(\overline{AB}\) and \(\overline{FH}\) are skew and \(\overline{AC}\) and \(\overline{EF}\) are skew.
Basic Facts About Parallel Lines
Property: If lines \(l\parallel m\) and \(m\parallel n\), then \(l\parallel n\).
If
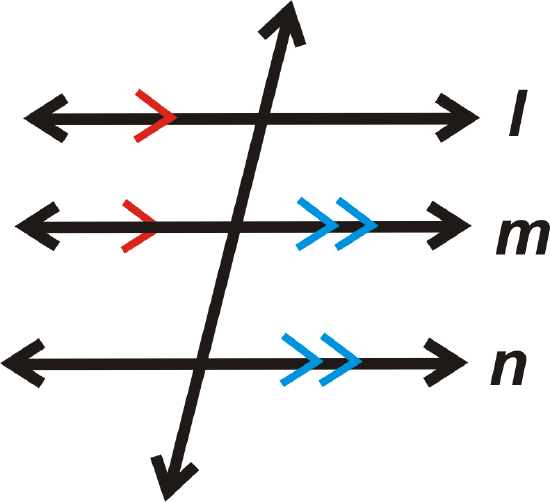
then
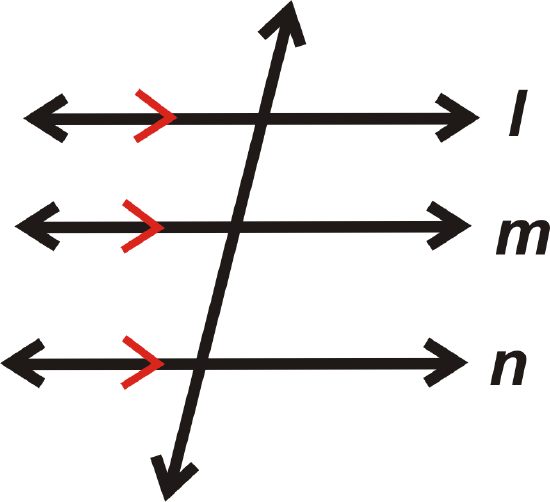
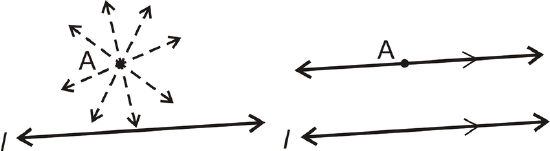
Postulate: For any line and a point not on the line, there is one line parallel to this line through the point. There are infinitely many lines that go through \(A\), but only one that is parallel to \(l\).
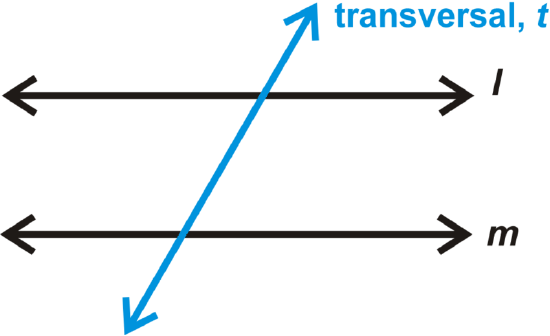
A transversal is a line that intersects two other lines. The area between \(l\) and \(m\) is the interior. The area outside \(l\) and \(m\) is the exterior.
What if you were given a pair of lines that never intersect and were asked to describe them? What terminology would you use?
Use the figure below for Examples \(\PageIndex{1}\) and \(\PageIndex{2}\). The two pentagons are parallel and all of the rectangular sides are perpendicular to both of them.
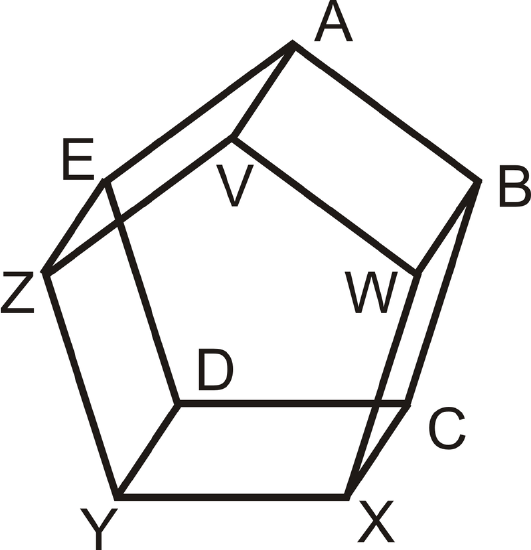
Example \(\PageIndex{1}\)
Find two pairs of skew lines.
Solution
\(\overline{ZV}\) and \(\overline{WB}\). \(\overline{YD}\) and \(\overline{VW}\)
Example \(\PageIndex{2}\)
For \(\overline{XY}\), how many parallel lines would pass through point \(D\)? Name this/these line(s).
Solution
One line, \(\overline{CD}\)
Example \(\PageIndex{3}\)
True or false: some pairs of skew lines are also parallel.
Solution
This is false, by definition skew lines are in different planes and parallel lines are in the same plane. Two lines could be skew or parallel (or neither), but never both.
Example \(\PageIndex{4}\)
Using the cube below, list a pair of parallel lines.
Solution
One possible answer is lines \(\overline{AB}\) and \(\overline{EF}\).
Example \(\PageIndex{5}\)
Using the cube below, list a pair of skew lines.
Solution
One possible answer is \(\overline{BD}\) and \(\overline{CG}\).
Review
- Which of the following is the best example of parallel lines?
- Railroad Tracks
- Lamp Post and a Sidewalk
- Longitude on a Globe
- Stonehenge (the stone structure in Scotland)
- Which of the following is the best example of skew lines?
- Roof of a Home
- Northbound Freeway and an Eastbound Overpass
- Longitude on a Globe
- The Golden Gate Bridge
Use the picture below for questions 3-5.
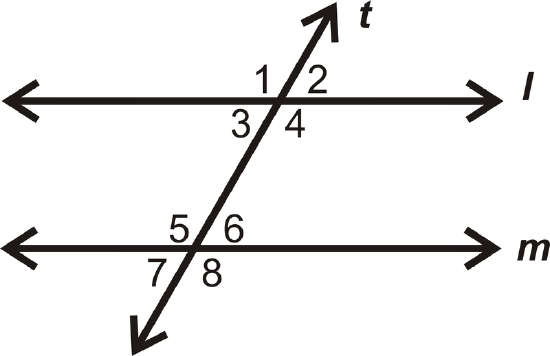
- If \(m\angle 2=55^{\circ}\), what other angles do you know?
- If \(m\angle 5=123^{\circ}\), what other angles do you know?
- Is \(l\parallel m\)? Why or why not?
For 6-10, determine whether the statement is true or false.
- If \(p\parallel q \)and \(q\parallel r\), then \(p\parallel r\).
- Skew lines are never in the same plane.
- Skew lines can be perpendicular.
- Planes can be parallel.
- Parallel lines are never in the same plane.
Review (Answers)
To see the Review answers, open this PDF file and look for section 3.1.
Resources
Vocabulary
| Term | Definition |
|---|---|
| parallel lines | Two or more lines that lie in the same plane and never intersect. Parallel lines will always have the same slope. |
| Skew lines | Skew lines are lines that are in different planes and never intersect. |
| transversal | A transversal is a line that intersects two other lines. |
| Parallel | Two or more lines are parallel when they lie in the same plane and never intersect. These lines will always have the same slope. |
| Skew | To skew a given set means to cause the trend of data to favor one end or the other |
Additional Resources
Interactive Element
Video: Proving Lines Parallel
Practice: Parallel and Skew Lines Discussion Questions
Study Aids: Lines and Angles Study Guide
Pratice: Parallel and Skew Lines
Real World: Short Circuits: How Parallel Circuits Work