4.16: HL
- Page ID
- 4813
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)HL Triangle Congruence
Hypotenuse-Leg Congruence Theorem
If the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent. This is called the Hypotenuse-Leg (HL) Congruence Theorem. Note that it will only work for right triangles.
If \(\Delta ABC\) and \(\Delta XYZ\) are both right triangles and \(\overline{AB}\cong \overline{XY}\) and \(\overline{BC}\cong \overline{YZ}\) then \(\Delta ABC\cong \Delta XYZ\).
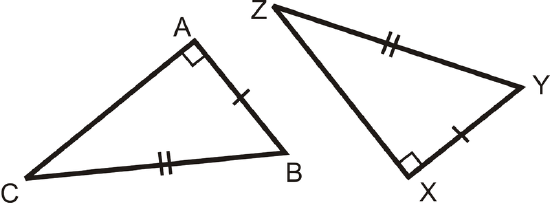
What if you were given two right triangles and provided with only the measure of their hypotenuses and one of their legs? How could you determine if the two right triangles were congruent?
Example \(\PageIndex{1}\)
Fill in the blanks in the proof below.
Given:
\(\overline{SV}\perp \overline{WU}\)
\(T\) is the midpoint of \(\overline{SV}\) and \(\overline{WU}\)
Prove: \(\overline{WS}\cong \overline{UV}\)
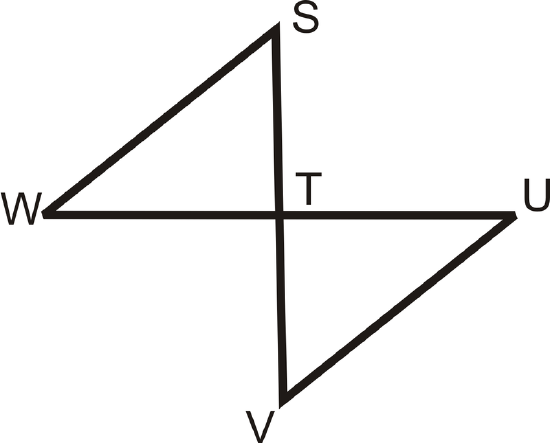
Solution
| Statement | Reason |
|---|---|
| 1. | 1. |
| 2. \(\angle STW\) and \(\angle UTV\) are right angles | 2. |
| 3. | 3. |
| 4. \(\overline{ST}\cong \overline{TV}\), \(\overline{WT}\cong \overline{TU}\) | 4. |
| 5. \(\Delta STW\cong \Delta UTV\) | 5. |
| 6. \(\overline{WS}\cong \overline{UV}\) | 6. |
| Statement | Reason |
|---|---|
| 1. \(\overline{SV}\perp \overline{WU}\) | 1. Given |
| 2. \(\angle STW\) and \(\angle UTV\) are right angles | 2. Definition of perpendicular lines. |
| 3. \(T\) is the midpoint of \(\overline{SV}\) and \(\overline{WU}\) | 3. Given |
| 4. \(\overline{ST}\cong \overline{TV}\), \(\overline{WT}\cong \overline{TU}\) | 4. Definition of midpoint |
| 5. \(\Delta STW\cong \Delta UTV\) | 5. SAS |
| 6. \(\overline{WS}\cong \overline{UV}\) | 6. CPCTC |
Note that even though these were right triangles, we did not use the HL congruence shortcut because we were not originally given that the two hypotenuses were congruent. The SAS congruence shortcut was quicker in this case.
Example \(\PageIndex{2}\)
Explain why the HL Congruence shortcut works.
The Pythagorean Theorem, which says, for any right triangle, this equation is true:
\((leg)^2+(leg)^2=(hypotenuse)^2\)
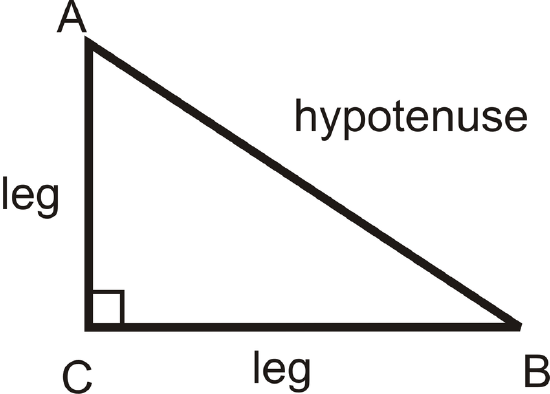
Solution
What this means is that if you are given two sides of a right triangle, you can always find the third. Therefore, if you know two sides of a right triangle are congruent to two sides of another right triangle, then you can conclude that the third sides are also congruent. If three pairs of sides are congruent, then we know the triangles are congruent by SSS.
Example \(\PageIndex{3}\)
What additional information would you need to prove that these two triangles were congruent using the HL Theorem?
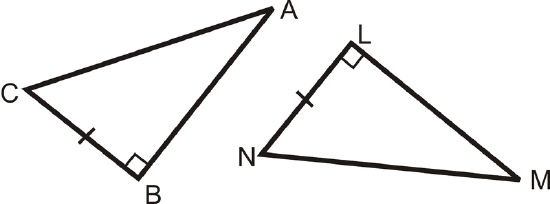
Solution
For HL, you need the hypotenuses to be congruent. \(\overline{AC}\cong MN\overline{AB}\).
Example \(\PageIndex{4}\)
Determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
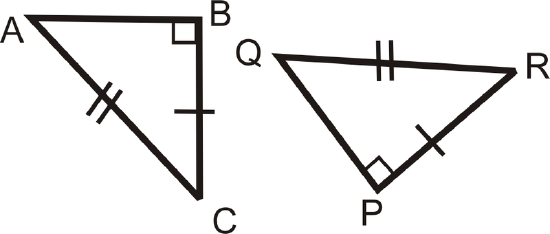
Solution
We know the two triangles are right triangles. The have one pair of legs that is congruent and their hypotenuses are congruent. This means that \(\Delta ABC\cong \Delta RQP\) by HL.
Example \(\PageIndex{5}\)
Determine the additional piece of information needed to show the two triangles are congruent by HL.
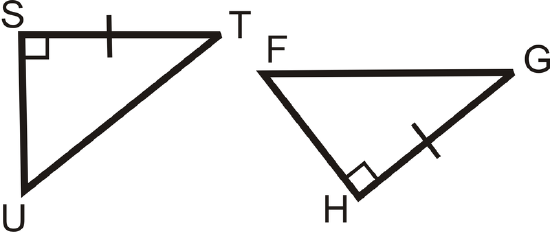
Solution
We already know one pair of legs is congruent and that they are right triangles. The additional piece of information we need is that the two hypotenuses are congruent, \(\overline{UT}\cong \overline{FG}\).
Review
Using the HL Theorem, what additional information do you need to prove the two triangles are congruent?
-
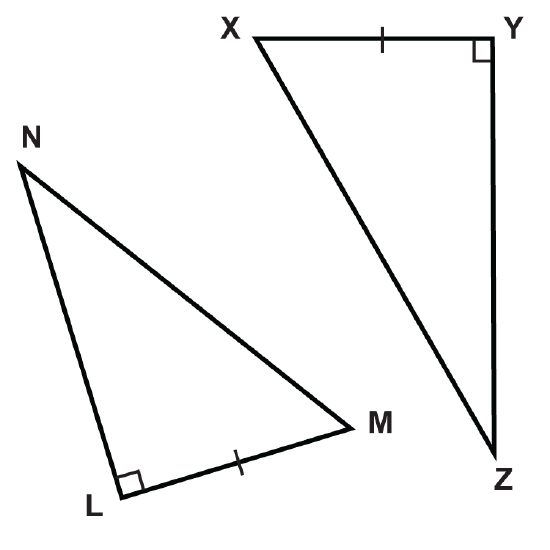
Figure \(\PageIndex{7}\) -
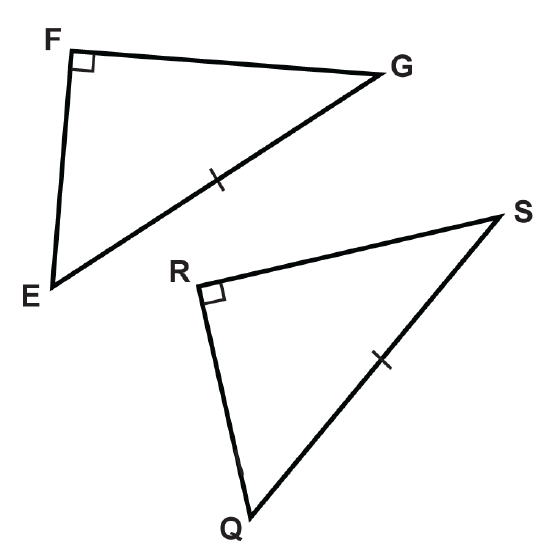
Figure \(\PageIndex{8}\) -
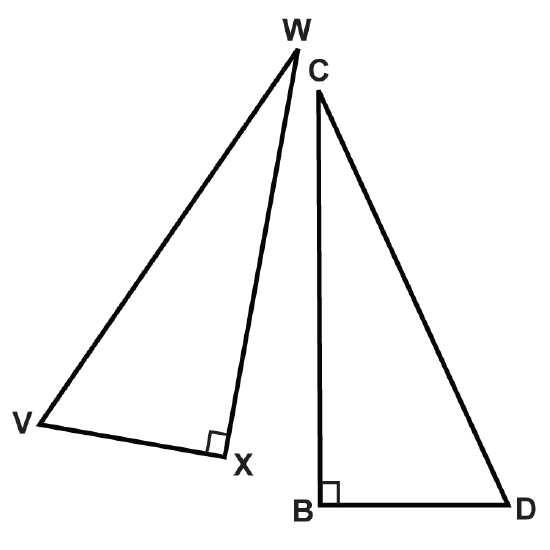
Figure \(\PageIndex{9}\)
The triangles are formed by two parallel lines cut by a perpendicular transversal. \(C\) is the midpoint of \(\overline{AD}\). Complete the proof to show the two triangles are congruent. Questions 4-7 are within the proof.
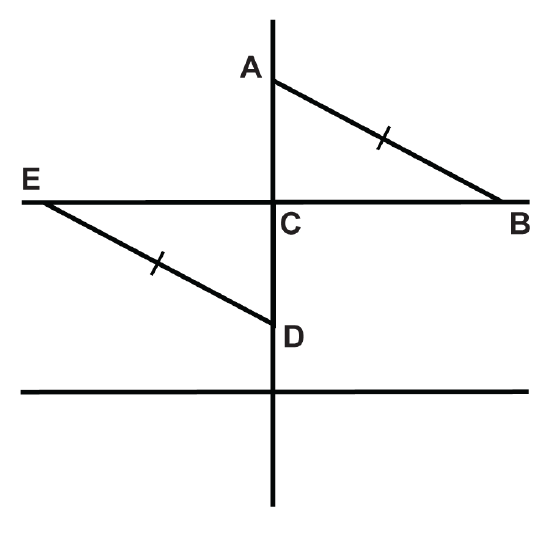
| Statement | Reason |
|---|---|
| 1. \(\angle ACB\) and \(\angle DCE\) are right angles. | (4.) |
| 2. (5.) | Definition of midpoint |
| 3. (6.) | Given |
| 4. \(\Delta ACD\cong \Delta DCE\) | (7.) |
Based on the following details, are the two right triangles definitively congruent? The statements do not build off of each other.
- The hypotenuses of two right triangles are congruent.
- Both sets of legs in the two right triangles are congruent.
- One set of legs are congruent in the two right triangles.
- The hypotenuses and one pair of legs are congruent in the two right triangles.
- One of the non right angles of the two right triangles is congruent.
- All of the angles of the two right triangles are congruent.
- All of the sides of the two right triangles are congruent.
- Both triangles have one leg that is twice the length of the other.
Resources
Vocabulary
| Term | Definition |
|---|---|
| hypotenuse | The side opposite the right angle in a right triangle. |
| legs | The two sides adjacent to the right angle. |
| right triangle | A triangle with exactly one right (\(90^{\circ}\)) angle. The two sides adjacent to the right angle are called legs and the side opposite the right angle is called the hypotenuse. |
| H-L (Hypotenuse-Leg) Congruence Theorem | If the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent. |
Additional Resources
Interactive Element
Video: HL Triangle Congruence Principles - Basic
Activities: HL Triangle Congruence Discussion Questions
Study Aids: Triangle Congruence Study Guide
Practice: HL
Real World: Final Drafts