4.31: Converse of the Pythagorean Theorem
- Page ID
- 4963
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify right triangles using the theorem.
Derive and Use the Converse of the Pythagorean Theorem

Brandon has just purchased his first home and is very anxious to plant a flower garden in a triangular section of the backyard. Brandon has inherited a metal fence that his grandfather had made many years ago and he would like to use it in his garden. The fence consists of two pieces that are welded together to form a right angle and another long straight piece. He knows that the pieces of fence will fit in the garden if his triangular garden is a right triangle.
“If only I could use the garden measurements of 29 feet, 20 feet and 29 feet to figure out if my garden space forms a right triangle, then I could use Grandpa’s fence.” he thought to himself.
In this concept, you will learn to derive and use the converse of the Pythagorean Theorem.
The Converse of the Pythagorean Theorem
The Pythagorean Theorem states that for a right triangle the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem can be modeled by the equation \(c^2=a^2+b^2\) where '\(c\)' represents the length of the hypotenuse, ‘a’ represents the length of one leg and '\(b\)' represents the length of the other leg.
The Pythagorean Theorem can be used to calculate the length of an unknown side of a right triangle. The Converse of the Pythagorean Theorem states that if the square of the length of one side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the angle opposite the longest side is a right angle. A triangle that contains a right angle is a right triangle.
Let’s look at the converse of the Pythagorean Theorem in action.
Determine whether or not the following triangles (which may not be drawn to scale) are right triangles. If the triangle is a right triangle, make any necessary changes to the triangle and draw it correctly.
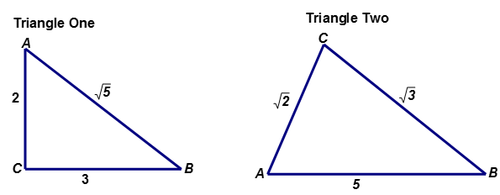
Let’s begin with Triangle One.
First, determine the longest side of the triangle.
The lengths of the sides are 2, 3 and \(\sqrt{5}\). The length of side \(BC\) is \(\sqrt{5}\approx 2.24\: units\). The longest side of the triangle is \(AB\) which will be the hypotenuse of the triangle if \(\Delta ABC\) is a right triangle.
Next, substitute the values \((2,\sqrt{5},3)\) for \((a,b,c)\) respectively into the equation \(c^2=a^2+b^2\).
\(\begin{align*}c^2&=a^2+b^2 \\ (3)^2&=(2)^2+(\sqrt{5})^2\end{align*}\)
Next, square each of the terms indicated in the equation.
\(\begin{align*}(3)^2&=(2)^2+(\sqrt{5})^2 \\ (3\times 3)&=(2\times 2)+(\sqrt{5}\times \sqrt{5})\end{align*}\)
Next, evaluate each of the squares.
\(\begin{align*}(3\times 3)&=(2\times 2)+(\sqrt{5}\times \sqrt{5}) \\ 9&=4+5\end{align*}\)
Then, simplify the right side of the equation by adding the numbers.
\(\begin{align*}9&=4+5 \\ 9&=9\end{align*}\)
Both sides of the equation are equal. The square of the length of one side of the triangle is equal to the sum of the squares of the lengths of the other two sides. Triangle One is a right triangle. The length of \(BC\) should be 3 and the length of AB should be \(\sqrt{5}\) since the right angle is located at C.
Let’s look at Triangle Two.
First, determine the longest side of the triangle.
The lengths of the sides are \(\sqrt{2}\),\(\sqrt{3}\) and 5. The length of side \(AC\) is \(\sqrt{2}, approximately 1.41 units in length. The length of side \(BC\) is \(\sqrt{3}\), approximately 1.73 units in length. The longest side of the triangle is AB which will be the hypotenuse of the triangle if \(\Delta ABC\) is a right triangle.
Next, substitute the values \((\sqrt{2},\sqrt{3},5)\) for \((a,b,c)\) respectively into the equation \(c^2=a^2+b^2\).
\(\begin{align*}c^2&=a^2+b^2 \\ (5)^2&=(\sqrt{2})^2+(\sqrt{3})^2\end{align*}\)
Next, square each of the terms indicated in the equation.
\(\begin{align*}(5)^2=(\sqrt{2})^2+(\sqrt{3})^2 \\ (5\times 5)=(\sqrt{2}\times \sqrt{2})+(\sqrt{3}\times \sqrt{3})\end{align*}\)
Next, evaluate each of the squares.
\(\begin{align*}(5\times 5)&=(\sqrt{2}\times \sqrt{2})+(\sqrt{3}\times \sqrt{3} \\ 25&=2+3\end{align*}\)
Then, simplify the right side of the equation by adding the numbers.
\(\begin{align*}25&=2+3 \\ 25&\neq 5\end{align*}\)
Both sides of the equation are not equal. The square of the length of one side of the triangle is NOT equal to the sum of the squares of the lengths of the other two sides. Triangle Two is not a right triangle.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Brandon’s flower garden and his metal fence. He needs to figure out if his garden space is a right triangle. How can Brandon figure this out using the measurements of the space?
Solution
First, determine the values for \((a,b,c) of a right triangle using the measurements of 29, 20 and 21 feet.
The longest side will represent '\(c\)' the hypotenuse.
\(a=20\)
\(b=21\)
\(c=29\)
Next, substitute the given values into the Pythagorean Theorem.
\(\begin{align*}c^2&=a^2+b^2 \\ (29)^2&=(20)^2+(21)^2\end{align*}\)
Next, square each of the terms indicated in the equation.
\(\begin{align*}(29)^2&=(20)^2+(21)^2 \\ (29\times 29)&=(20\times 20)+(21\times 21)\end{align*}\)
Next, evaluate each of the squares and simplify the equation.
\(\begin{align*}(29\times 29)&=(20\times 20)+(21\times 21) \\ 841&=400+441 \\ 841&=841\end{align*}\)
The square of the length of one side of the triangle is equal to the sum of the squares of the lengths of the other two sides. The garden is a right triangle.
Brandon can use his Grandpa’s fence for his flower garden.
Example \(\PageIndex{2}\)
Are the set of numbers \((5, 8, 10)\) the lengths of the sides of a right triangle?
Solution
First, determine the values for each side of the right triangle. The length of the longest side will represent ‘\(c\),’ the hypotenuse. The other two lengths will represent the lengths of the legs ‘\(a’ and ‘\(b\).’
\(a=5\)
\(b=8\)
\(c=10\)
Next, substitute the given values into the Pythagorean Theorem.
\(\begin{align*}c^2&=a^2+b^2 \\ (10)^2&=(5)^2+(8)^2\end{align*}\)
Next, square each of the terms indicated in the equation.
\(\begin{align*}(10)^2&=(5)^2+(8)^2 \\ (10\times 10)&=(5\times 5)+(8\times 8)\end{align*}\)
Next, evaluate each of the squares.
\(\begin{align*}(10\times 10)&=(5\times 5)+(8\times 8) \\ 100&=25+64\end{align*}\)
Then, simplify the right side of the equation by adding the numbers.
\(\begin{align*}100&=25+64 \\ 100&\neq 89\end{align*}\)
Both sides of the equation are not equal. The square of the length of one side of the triangle is NOT equal to the sum of the squares of the lengths of the other two sides.
The set of numbers \((5, 8, 10)\) are not the lengths of the sides of a right triangle.
Example \(\PageIndex{3}\)
Is the following triangle (which may or may not be drawn to scale) a right triangle?
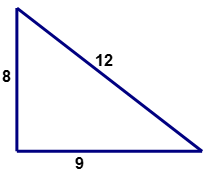
Solution
First, determine the values for \((a,b,c)\) of a right triangle. The longest side will represent '\(c\)' the hypotenuse.
\(a=8\)
\(b=9\)
\(c=12\)
Next, substitute the given values into the Pythagorean Theorem.
\(\begin{align*}c^2&=a^2+b^2 \\ (12)^2&=(8)^2+(9)^2\end{align*}\)
Next, square each of the terms indicated in the equation.
\(\begin{align*}(12)^2&=(8)^2+(9)^2 \\ (12\times 12)&=(8\times 8)+(9\times 9)\end{align*}\)
Next, evaluate each of the squares.
\(\begin{align*}(12\times 12)&=(8\times 8)+(9\times 9) \\ 144&=64+81\end{align*}\)
Then, simplify the right side of the equation by adding the numbers.
\(\begin{align*}144&=64+81 \\ 144&\neq 145\end{align*}\)
Both sides of the equation are not equal. The square of the length of one side of the triangle is NOT equal to the sum of the squares of the lengths of the other two sides. The triangle is not a right triangle.
Example \(\PageIndex{4}\)
Is the following triangle (which may or may not be drawn to scale) a right triangle?
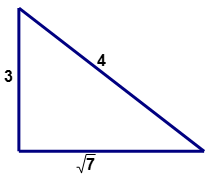
Solution
First, determine the values for \((a,b,c)\) of a right triangle. The longest side will represent '\(c\)' the hypotenuse.
\(\begin{align*}\sqrt{7}&\approx 2.65 \\ a&=3 \\ b&=\sqrt{7}\\ c&=4\end{align*}\)
Next, substitute the given values into the Pythagorean Theorem.
\(\begin{align*}c^2&=a^2+b^2 \\ (4)^2&=(3)^2+(\sqrt{7})^2\end{align*}\)
Next, square each of the terms indicated in the equation.
\(\begin{align*}(4)^2&=(3)^2+(\sqrt{7})^2 \\ (4\times 4)&=(3\times 3)+(\sqrt{7}\times \sqrt{7})\end{align*}\)
Next, evaluate each of the squares.
\(\begin{align*}(4\times 4)&=(3\times 3)+(\sqrt{7}\times \sqrt{7} \\ 16&=9+7\end{align*}\)
Then, simplify the right side of the equation by adding the numbers.
\(\begin{align*} 16&=9+7 \\ 16&=16\end{ailgn*}\)
Both sides of the equation are equal. The square of the length of one side of the triangle is equal to the sum of the squares of the lengths of the other two sides. The triangle is a right triangle.
Review
Think about what you have learned about the Pythagorean Theorem and answer true or false for the following questions.
1. The Pythagorean Theorem will work for an acute triangle with all \(60^{\circ}\) angles.
2. The Pythagorean Theorem will work for a right triangle.
3. The Pythagorean Theorem will only work if the triangle is a right triangle.
4. The legs of a right triangle are considered the two shorter sides of the right triangle.
5. The hypotenuse is the longest side of a right triangle.
6. The converse of the Pythagorean Theorem is used to find the angle measures of an obtuse triangle.
7. A Pythagorean Triple is when you multiply all of the angle measures by three.
8. You can use the Pythagorean Theorem to figure out if the side lengths of a triangle make it a right triangle or not.
Identify whether or not each of the following values is a Pythagorean Triple. Write yes or no for your answer.
9. \((4, 5, 6)\)
10. \((6, 8, 10)\)
11. \((5, 6, 9)\)
12. \((9, 12, 15)\)
13. \((30, 40, 55)\)
14. \((21, 28, 35)\)
15. \((12, 16, 20)\).
Vocabulary
| Term | Definition |
|---|---|
| directrix | The directrix of a parabola is the line that the parabola seems to curve away from. All points on a parabola are equidistant from the focus of the parabola and the directrix of the parabola. |
| focus | The focus of a parabola is the point that "anchors" a parabola. Any point on the parabola is exactly the same distance from the focus as from the directrix. |
| Hypotenuse | The hypotenuse of a right triangle is the longest side of the right triangle. It is across from the right angle. |
| Legs of a Right Triangle | The legs of a right triangle are the two shorter sides of the right triangle. Legs are adjacent to the right angle. |
| Parabola | A parabola is the characteristic shape of a quadratic function graph, resembling a "U". |
| Pythagorean Theorem | The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle, given by \(a^2+b^2=c^2\), where a and b are legs of the triangle and c is the hypotenuse of the triangle. |
| Pythagorean Triple | A Pythagorean Triple is a set of three whole numbers a,b and c that satisfy the Pythagorean Theorem, \(a^2+b^2=c^2\). |
| Right Triangle | A right triangle is a triangle with one 90 degree angle. |
Additional Resources
Video: The Pythagorean Theorem and The Converse of the Pythagorean Theorem
Practice: Converse of the Pythagorean Theorem

