5.21: Area of Regular and Irregular Polygons
- Page ID
- 5005
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Half the apothem times the perimeter.
Area of Regular Polygons
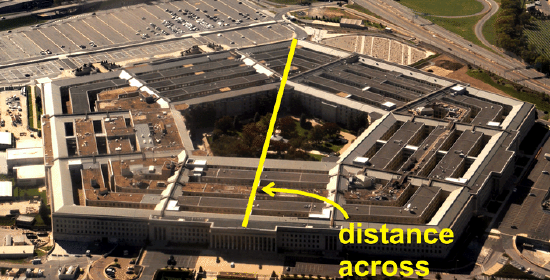
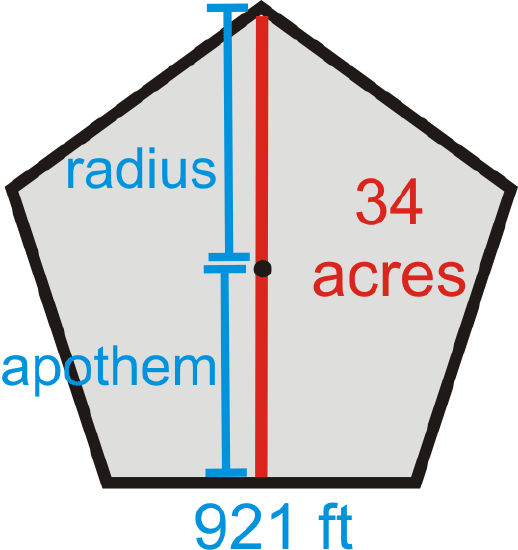
What if you were asked to find the distance across The Pentagon in Arlington, VA? The Pentagon, which also houses the Department of Defense, is composed of two regular pentagons with the same center. The entire area of the building is 29 acres (40,000 square feet in an acre), with an additional 5 acre courtyard in the center. The length of each outer wall is 921 feet. What is the total distance across the pentagon? Round your answer to the nearest hundredth.
A regular polygon is a polygon with congruent sides and angles. Recall that the perimeter of a square is 4 times the length of a side because each side is congruent. We can extend this concept to any regular polygon.
Perimeter of a Regular Polygon: If the length of a side is s and there are \(n\) sides in a regular polygon, then the perimeter is \(P=ns\).
In order to find the area of a regular polygon, we need to define some new terminology. First, all regular polygons can be inscribed in a circle. So, regular polygons have a center and radius, which are the center and radius of the circumscribed circle. Also like a circle, a regular polygon will have a central angle formed. In a regular polygon, however, the central angle is the angle formed by two radii drawn to consecutive vertices of the polygon. In the picture below, the central angle is \(\angle BAD\). Also, notice that \(\Delta BAD\) is an isosceles triangle. Every regular polygon with n sides is formed by n isosceles triangles. The height of these isosceles triangles is called the apothem.
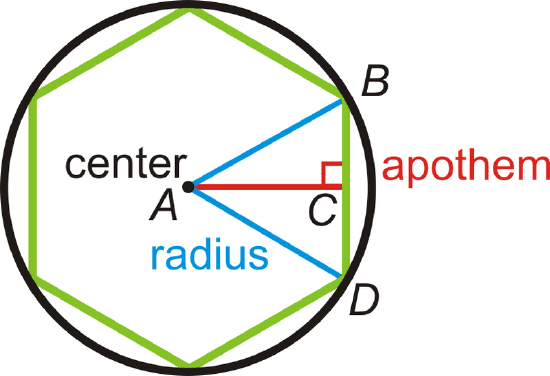
The area of each triangle is \(A_{\Delta} =\dfrac{1}{2}bh=\dfrac{1}{2}sa\), where s is the length of a side and a is the apothem. If there are n sides in the regular polygon, then it is made up of n congruent triangles.
Area of a Regular Polygon: If there are n sides with length s in a regular polygon and a is the apothem, then \(A=\dfrac{1}{2}asn\) or \(A=\dfrac{1}{2}aP\), where \(P\) is the perimeter.
Calculating the Perimeter
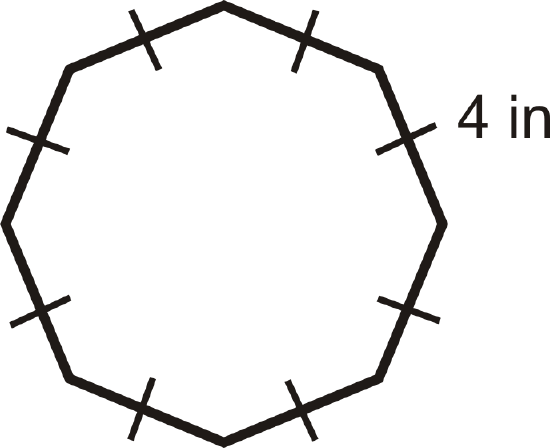
What is the perimeter of a regular octagon with 4 inch sides?
If each side is 4 inches and there are 8 sides, that means the perimeter is \(8(4\text{ in }) = 32\text{ inches }\).
Finding Side Lengths
The perimeter of a regular heptagon is 35 cm. What is the length of each side?
If \(P=ns\), then \(35\text{ cm }=7s\). Therefore, \(s=5\text{ cm }\).
Finding the Length of the Apothem
Find the length of the apothem in the regular octagon. Round your answer to the nearest hundredth.
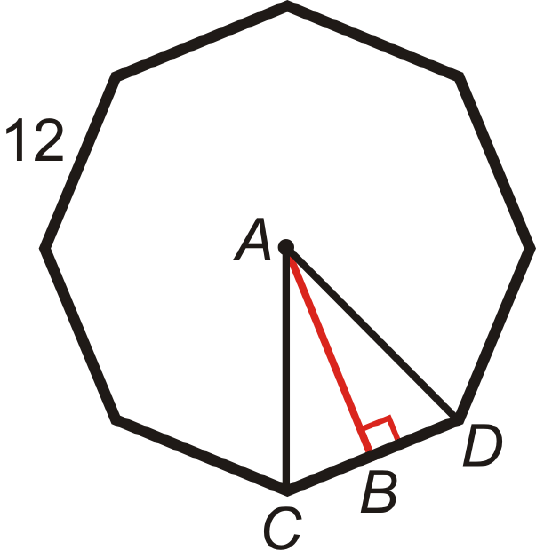
To find the length of the apothem, AB, you will need to use the trig ratios. First, find \(m\angle CAD\). There are \(360^{\circ}\) around a point, so \(m\angle CAD=\dfrac{360^{\circ}}{8}=45^{\circ}\). Now, we can use this to find the other two angles in \(\Delta CAD\). m\angle ACB\) and m\angle ADC\) are equal because \Delta CAD\) is a right triangle.
\(\begin{aligned}m\angle CAD+m\angle ACB+m\angle ADC&=180^{\circ} \\ 45^{\circ}+2m\angle ACB&=180^{\circ} \\ 2m\angle ACB&=135^{\circ} \\ m\angle ACB&=67.5^{\circ}\end{aligned}\)
To find AB, we must use the tangent ratio. You can use either acute angle.
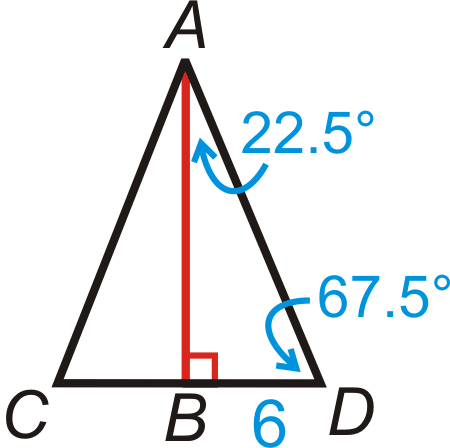
\(\begin{aligned}tan67.5^{\circ}&=\dfrac{AB}{6} \\ AB&=6\cdot tan67.5^{\circ}\approx 14.49\end{aligned}\)
Pentagon Problem Revisited
From the picture below, we can see that the total distance across the Pentagon is the length of the apothem plus the length of the radius. If the total area of the Pentagon is 34 acres, that is 2,720,000 square feet. Therefore, the area equation is \(2720000=\dfrac{1}{2}a(921)(5)\) and the apothem is 590.66 ft. To find the radius, we can either use the Pythagorean Theorem, with the apothem and half the length of a side or the sine ratio. Recall from Example 5, that each central angle in a pentagon is \(72^{\circ}\), so we would use half of that for the right triangle.
\(sin36^{\circ}=\dfrac{460.5}{r} \rightarrow r=\dfrac{460.5}{sin36^{\circ}}\approx 783.45\text{ ft }\)
Therefore, the total distance across is \(590.66+783.45=1374.11\: ft\).
Example \(\PageIndex{1}\)
Find the area of the regular octagon in Example C.
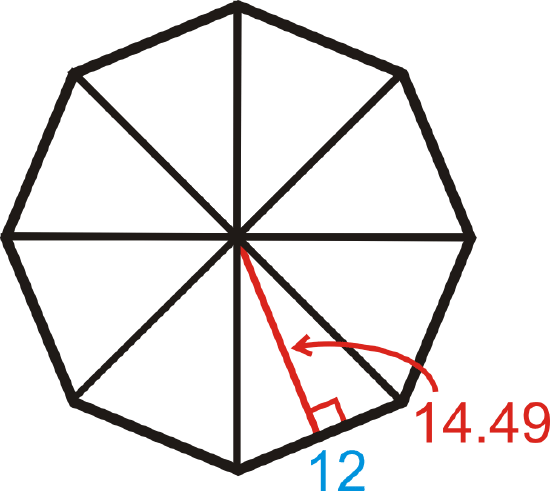
Solution
The octagon can be split into 8 congruent triangles. So, if we find the area of one triangle and multiply it by 8, we will have the area of the entire octagon.
\(A_{octagon}=8(12\cdot 12\cdot 14.49)=695.52 units^2\)
Example \(\PageIndex{2}\)
Find the area of the regular polygon with radius 4.
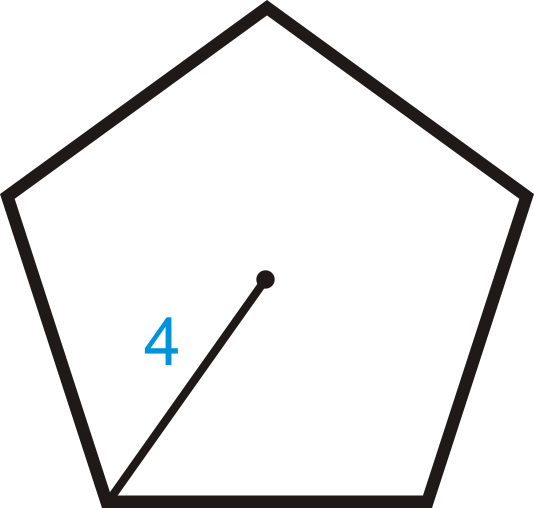
Solution
INSERTB In this problem we need to find the apothem and the length of the side before we can find the area of the entire polygon. Each central angle for a regular pentagon is \(\dfrac{360^{\circ}}{5}=72^{\circ}\). So, half of that, to make a right triangle with the apothem, is \(36^{\circ}\). We need to use sine and cosine.
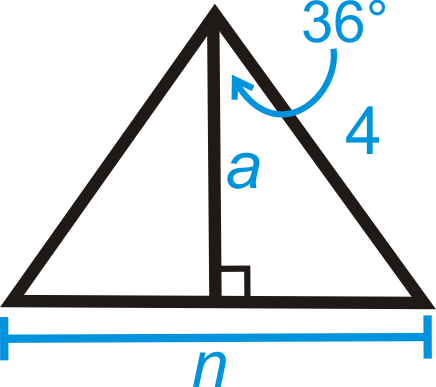
\(\begin{array}{rlr}
\sin 36^{\circ} & =\frac{.5 n}{4} & \cos 36^{\circ}&=\frac{a}{4} \\
4 \sin 36^{\circ} & =\frac{1}{2} n & 4 \cos 36^{\circ}&=a \\
8 \sin 36^{\circ} & =n & a &\approx 3.24 \\
n & \approx 4.7
\end{array}\)
Using these two pieces of information, we can now find the area. \(A=12(3.24)(5)(4.7)\approx 38.07 units^2\).
Example \(\PageIndex{3}\)
The area of a regular hexagon is \(54\sqrt{3}\) and the perimeter is 36. Find the length of the sides and the apothem.
Solution
Plug in what you know into both the area and the perimeter formulas to solve for the length of a side and the apothem.
\(\begin{array}{rlrl}
P&=s n & A & =\frac{1}{2} a P \\
36&=6 s & 54 \sqrt{3} & =\frac{1}{2} a(36) \\
s&=6 & 54 \sqrt{3} & =18 a \\
3 \sqrt{3} &=a
\end{array}\)
Review
Use the regular hexagon below to answer the following questions. Each side is 10 cm long.
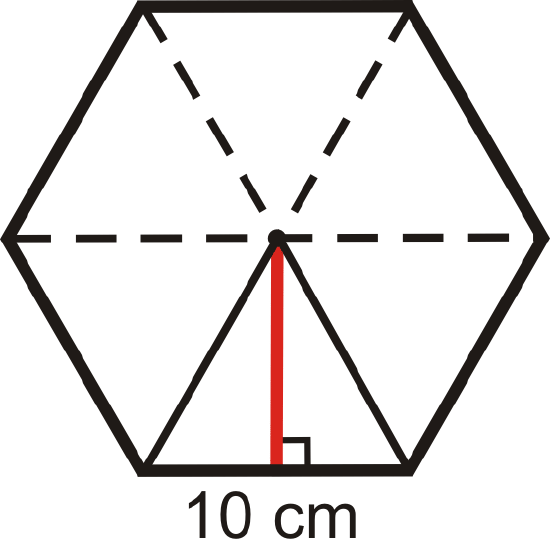
- Each dashed line segment is a(n) ________________.
- The red line segment is a(n) __________________.
- There are _____ congruent triangles in a regular hexagon.
- In a regular hexagon, all the triangles are _________________.
- Find the radius of this hexagon.
- Find the apothem.
- Find the perimeter.
- Find the area.
Find the area and perimeter of each of the following regular polygons. Round your answer to the nearest hundredth.
-
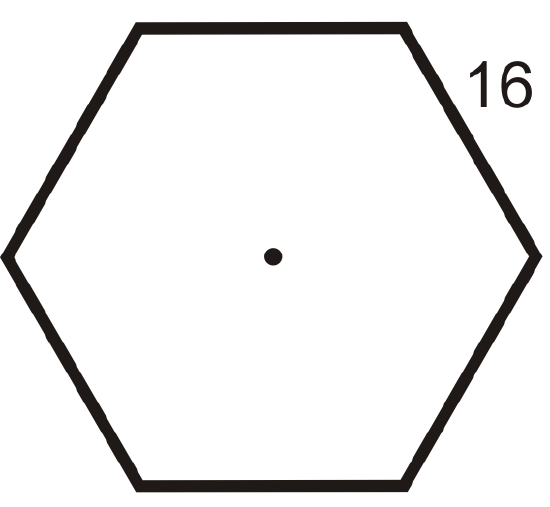
Figure \(\PageIndex{11}\) -
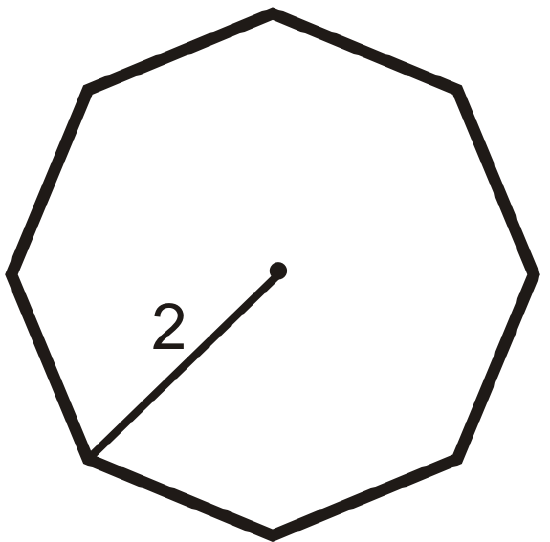
Figure \(\PageIndex{12}\) -
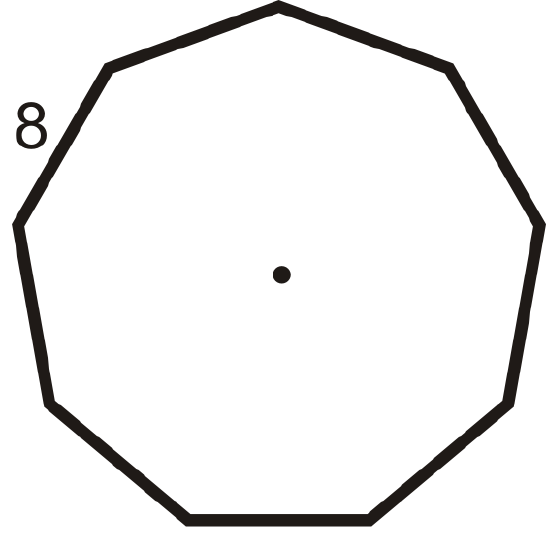
Figure \(\PageIndex{13}\) -
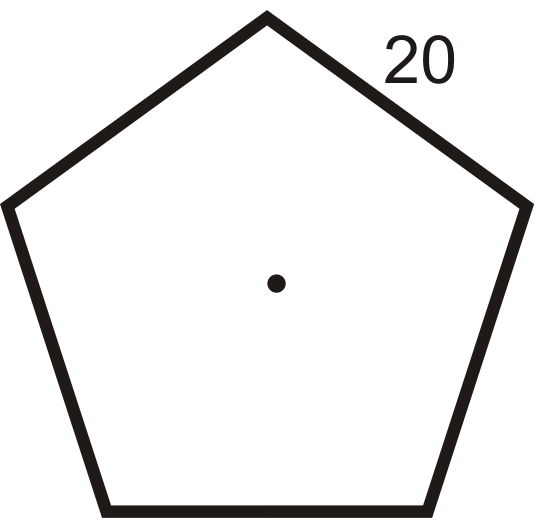
Figure \(\PageIndex{14}\) - If the perimeter of a regular decagon is 65, what is the length of each side?
- A regular polygon has a perimeter of 132 and the sides are 11 units long. How many sides does the polygon have?
- The area of a regular pentagon is \(440.44\text{ in }^2\) and the perimeter is 80 in. Find the length of the apothem of the pentagon.
- The area of a regular octagon is \(695.3\text{ cm }^2\) and the sides are 12 cm. What is the length of the apothem?
A regular 20-gon and a regular 40-gon are inscribed in a circle with a radius of 15 units.
- Challenge Derive a formula for the area of a regular hexagon with sides of length s. Your only variable will be s. HINT: Use 30-60-90 triangle ratios.
- Challenge in the following steps you will derive an alternate formula for finding the area of a regular polygon with n sides.
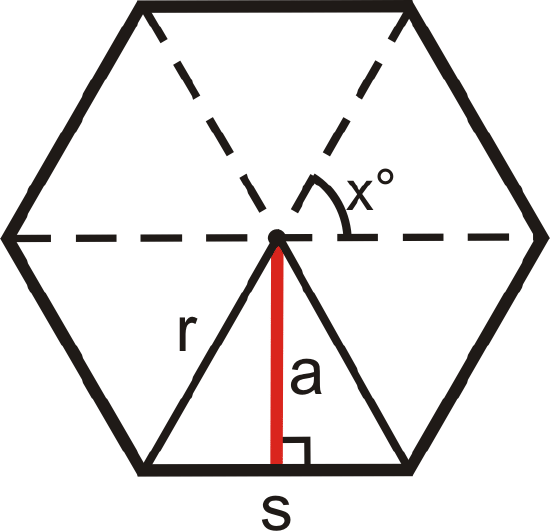
We are going to start by thinking of a polygon with n sides as n congruent isosceles triangles. We will find the sum of the areas of these triangles using trigonometry. First, the area of a triangle is \(\dfrac{1}{2}bh\). In the diagram to the right, this area formula would be \(\dfrac{1}{2}sa\), where s is the length of a side and a is the length of the apothem. In the diagram, \(x\) represents the measure of the vertex angle of each isosceles triangle.
- The apothem, a, divides the triangle into two congruent right triangles. The top angle in each is \(\dfrac{x^{\circ}}{2}\). Find \(sin(\dfrac{x^{\circ}}{2})\) and \(cos(\dfrac{x^{\circ}}{2})\).
- Solve your sin equation to find an expression for s in terms of \(r\) and \(x\).
- Solve your cos equation to find an expression for a in terms of \(r\) and \(x\).
- Substitute these expressions into the equation for the area of one of the triangles, \dfrac{1}{2}sa\).
- Since there will be n triangles in an n-gon, you need to multiply your expression from part d by n to get the total area.
- How would you tell someone to find the value of \(x\) for a regular n-gon?
Use the formula you derived in problem 18 to find the area of the regular polygons described in problems 19-22. Round your answers to the nearest hundredth.
- Decagon with radius 12 cm.
- 20-gon with radius 5 in.
- 15-gon with radius length 8 cm.
- 45-gon with radius length 7 in.
Review (Answers)
To view the Review answers, open this PDF file and look for section 10.12.
Additional Resources
Interactive Element
Video: Area of Regular Polygons Principles
Practice: Area of Regular and Irregular Polygons

