5.20: Regular and Irregular Polygons
- Page ID
- 5004
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Understand and identify regular and irregular polygons.

Logan has been tracing street signs around his city. He is preparing to trace the above street sign. He outlines the shape and he draws the round edges as straight lines. Will the resulting shape be a regular or irregular polygon, and what type of polygon will it be?
In this concept, you will learn how to determine if a polygon is regular or irregular.
Determining if Polygons are Regular or Irregular
A polygon can have a certain number of sides, but the sides do not necessarily have to be the same length. Both of the polygons below are pentagons because they both have five angles and sides, but look at the differences.
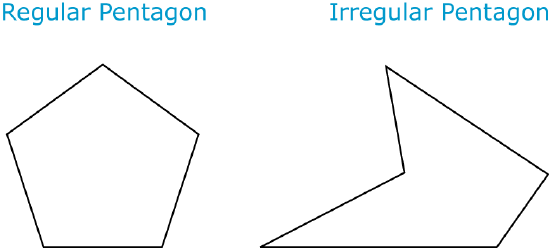
In the first pentagon, all of the angles are congruent and all of the sides are congruent. In the second pentagon, the angles have different measures and the sides have different lengths.
A regular polygon has congruent angles and congruent sides. Any polygon can be a regular polygon.
Look at the regular polygons below.
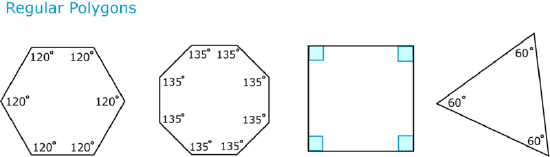
As you can see, a regular hexagon has six congruent sides and six congruent angles. A regular hexagon, no matter how long its sides, will always have angles that measure \(120^{\circ}\).
A regular octagon has eight congruent angles and eight congruent sides. Every regular octagon has the same angle measures.
The term “regular rectangle” is not usually used because a rectangle with congruent sides is actually a square. The four angles in a square are always \(90^{\circ}\), and their sum is always \(360^{\circ}\). However, there is a special name for a “regular triangle.” A triangle with three congruent sides is called an equilateral triangle. Its three angles are always \(60^{\circ}\), and their sum is always \(180^{\circ}\).
Any polygon that does not have all congruent sides is an irregular polygon. Irregular polygons can still be pentagons, hexagons and nonagons, but they do not have congruent angles or equal sides. Here are some examples of irregular polygons.
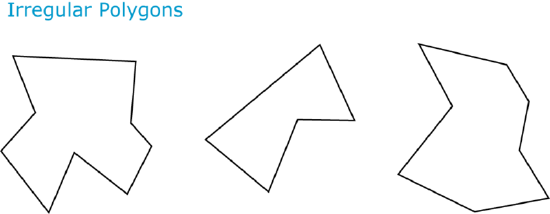
In these polygons, some sides are clearly longer than others and some angles are wider than others, so they must be irregular. Notice that irregular polygons tend to look uneven or lopsided, while regular polygons look more orderly and symmetrical.
Let’s look at an example of identifying irregular and regular polygons.
Identify the polygon below and tell whether it is regular or irregular.
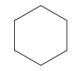
First, count the number of sides.
The shape has 6 sides.
Next, determine if the sides are congruent.
The sides are congruent.
Then, label the polygon as regular or irregular.
Regular.
The answer is that the polygon is a regular hexagon.
When lines intersect in the geometric plane, they form polygons. Apply what you know in order to classify these polygons. Find side lengths, or solve for unknown angle measures.
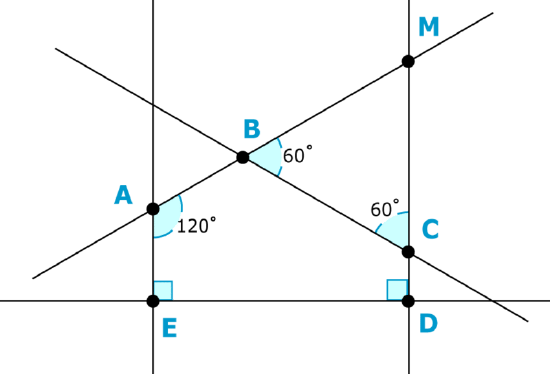
The intersection of these five lines has created several different polygons. First, let’s identify them.
The largest is \(AMDE\). Within this figure there are two figures.
One is figure \(ABCDE\). \(ABCDE\) has five angles and five sides, so it is a pentagon. Two of its angles measure \(90^{\circ}\), and one measures \(120^{\circ} \) Which means that the polygon is an irregular pentagon. In order to find the measures of the two remaining angles, you need to take a look at the third figure.
The third figure is triangle \(MBC\). It has two \(60^{\circ}\) angles. Angles \(ABC\) and \(MBC\) are supplementary. In other words, together they form a straight line. A straight line measures \(180^{\circ}\). Therefore the sum of these two angles is 180^{\circ}\). Simply subtract to find the measure of \(ABC\).
\(180−60=120^{\circ}\)
Angle ABC is \(120^{\circ}\).
Now let’s find the measure of angle \(BCD\). You now know four of the five angles in figure \(ABCDE\). Because this is a pentagon, you also know that its interior angles must have a sum of \(540^{\circ}\). You can set up an equation to find the measure of the unknown angle.
\(\begin{aligned} 90+90+120+120+\angle BCD&=540^{\circ} \\ 420+\angle BCD&=540^{\circ} \\ \angle BCD&=540−420 \\ \angle BCD&=120^{\circ} \end{aligned}\)
The fifth and final angle must measure \(120^{\circ}\). Let’s add up all of the angles in the pentagon to be sure they total \(540^{\circ}\).
\(90+90+120+120+120=540^{\circ}\)
There is still one unknown angle, angle AMD\). There are two different ways to find the measure of the third angle in triangle \(BMD\). You know that the three angles in a triangle have a sum of \(180^{\circ}\). It is also the fourth angle in quadrilateral \(AMDE\), and you know that the four angles in a quadrilateral have a sum of \(360^{\circ}\). You can set up an equation to find \(AMD\).
\(\begin{aligned}60+60+\angle AMD&=180^{\circ} \\ 120+\angle AMD&=180^{\circ} \\ \angle AMD&=180−120 \\ \angle AMD&=60^{\circ}\end{aligned}\)
Example \(\PageIndex{1}\)

Earlier, you were given a problem about Logan and the above street sign.
If he traces the shape of the sign, will the resulting shape be a regular or irregular polygon, and what type of polygon will it be?
Solution
First, count the number of sides.
The shape has 6 sides.
Next, determine if the sides are congruent.
The sides are not congruent.
Then, label the polygon as regular or irregular.
Irregular.
The answer is that the polygon is an irregular hexagon.
Example \(\PageIndex{2}\)
Name this figure.

Solution
First, count the number of sides.
The shape has 5 sides.
Next, determine if the sides are congruent.
The sides are not congruent.
Then, label the polygon as regular or irregular.
Irregular.
The answer is the polygon is an irregular pentagon.
Example \(\PageIndex{3}\)
Name this figure.

Solution
First, count the number of sides.
The shape has 7 sides.
Next, determine if the sides are congruent.
The sides are not congruent.
Then, label the polygon as regular or irregular.
Irregular.
The answer is the polygon is an irregular heptagon.
Example \(\PageIndex{4}\)
Classify the figure as irregular or regular and identify the polygon.
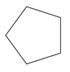
Solution
First, count the number of sides.
The shape has 5 sides.
Next, determine if the sides are congruent.
The sides appear to be congruent.
Then, label the polygon as regular or irregular.
Regular.
The answer is that the polygon is a regular pentagon.
Example \(\PageIndex{5}\)
Identify the polygon.
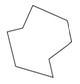
Solution
First, count the number of sides.
The shape has 8 sides.
Next, determine if the sides are congruent.
The sides are not congruent.
Then, label the polygon as regular or irregular.
Irregular.
The answer is that the polygon is an irregular octagon.
Review
Identify each quadrilateral by its description.
- A quadrilateral with one pair of parallel sides.
- A quadrilateral with opposites sides congruent and parallel, with four right angles.
- A quadrilateral with four congruent parallel sides and four right angles.
- A rectangle with four congruent parallel sides.
Identify the polygons in the diagram. Then find the measures of the unknown angles.
-
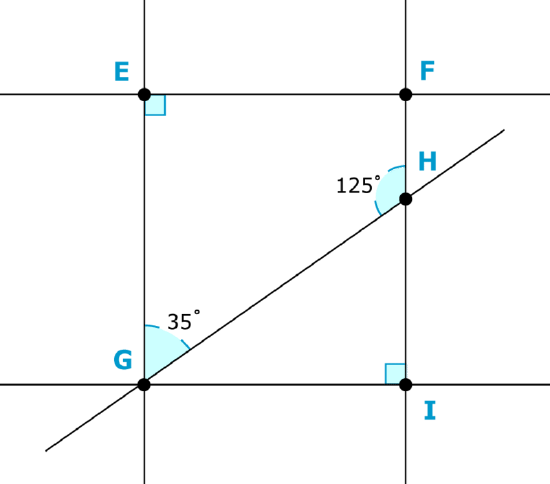
Figure \(\PageIndex{12}\)
Answer true or false for each of the following questions.
- A rhombus is always a square.
- A parallelogram has opposite sides that are parallel.
- A rectangle is a type of parallelogram.
- Squares, rectangles and rhombi are parallelograms with four right angles.
- A trapezoid has four right angles.
- A trapezoid has one pair of parallel sides.
- A regular polygon has congruent sides and angles.
- A pentagon can not be an irregular polygon.
Identify each polygon below.
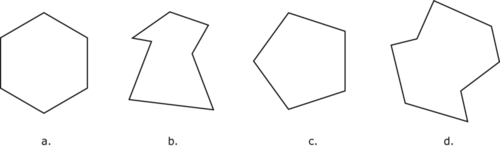
- a
- b
- c
- d
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.11.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Parallelogram | A parallelogram is a quadrilateral with two pairs of parallel sides. |
| Polygon | A polygon is a simple closed figure with at least three straight sides. |
| Quadrilateral | A quadrilateral is a closed figure with four sides and four vertices. |
| Rectangle | A rectangle is a quadrilateral with four right angles. |
| Rhombus | A rhombus is a quadrilateral with four congruent sides. |
| Square | A square is a polygon with four congruent sides and four right angles. |
Additional Resources
Interactive Element
Video: Introduction to Polygons
Practice: Regular and Irregular Polygons
Real World: A Perfect Pentagon

