5.19: Quadrilateral Classification in the Coordinate Plane
- Page ID
- 5003
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify and calculate area of shapes based on coordinates on a plane.
Quadrilateral Classification
What if you were given a quadrilateral in the coordinate plane? How could you determine if that quadrilateral qualifies as one of the special quadrilaterals: parallelograms, squares, rectangles, rhombuses, kites, or trapezoids?
When working in the coordinate plane, you will sometimes want to know what type of shape a given shape is. You should easily be able to tell that it is a quadrilateral if it has four sides. But how can you classify it beyond that?
First you should graph the shape if it has not already been graphed. Look at it and see if it looks like any special quadrilateral. Do the sides appear to be congruent? Do they meet at right angles? This will give you a place to start.
Once you have a guess for what type of quadrilateral it is, your job is to prove your guess. To prove that a quadrilateral is a parallelogram, rectangle, rhombus, square, kite or trapezoid, you must show that it meets the definition of that shape OR that it has properties that only that shape has.
If it turns out that your guess was wrong because the shape does not fulfill the necessary properties, you can guess again. If it appears to be no type of special quadrilateral then it is simply a quadrilateral.
The examples below will help you to see what this process might look like.
Classifying Parallelograms
Determine what type of parallelogram TUNE is: \(T(0,10),\: U(4,2),\: N(−2,−1),\: and\: E(−6,7)\).
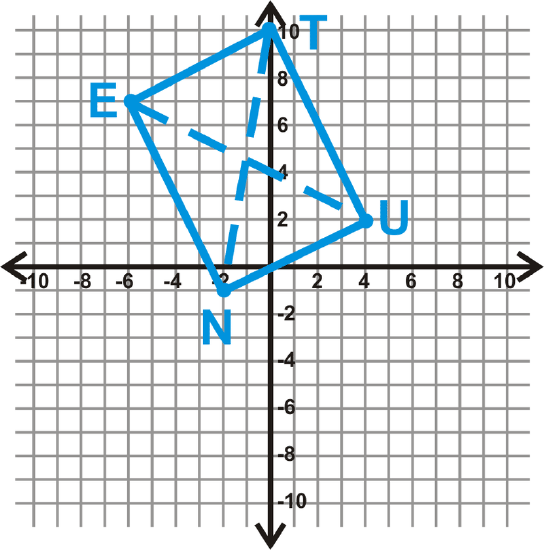
This looks like a rectangle. Let’s see if the diagonals are equal. If they are, then TUNE is a rectangle.
\(\begin{aligned}
E U &=\sqrt{(-6-4)^{2}+(7-2)^{2}} & T N &=\sqrt{(0+2)^{2}+(10+1)^{2}} \\
&=\sqrt{(-10)^{2}+5^{2}} & &=\sqrt{2^{2}+11^{2}} \\
&=\sqrt{100+25} & &=\sqrt{4+121} \\
&=\sqrt{125} & &=\sqrt{125}
\end{aligned}\)
If the diagonals are also perpendicular, then \(TUNE\) is a square.
\(\text { Slope of } E U=\dfrac{7-2}{-6-4}=-\dfrac{5}{10}=-\dfrac{1}{2} \quad \text { Slope of } T N=\dfrac{10-(-1)}{0-(-2)}=\dfrac{11}{2}\)
The slope of \(EU\) \(\neq\) slope of \(TN\), so \(TUNE\) is a rectangle.
Determining if a Quadrilateral is a Parallelogram
A quadrilateral is defined by the four lines \(y=2x+1\), \(y=−x+5\), \(y=2x−4\), and \(y=−x−5\). Is this quadrilateral a parallelogram?
To check if its a parallelogram we have to check that it has two pairs of parallel sides. From the equations we can see that the slopes of the lines are 2, −1, 2 and −1. Because two pairs of slopes match, this shape has two pairs of parallel sides and is a parallelogram.
Determining Types of Quadrilaterals
Determine what type of quadrilateral \(RSTV\) is. Simplify all radicals.
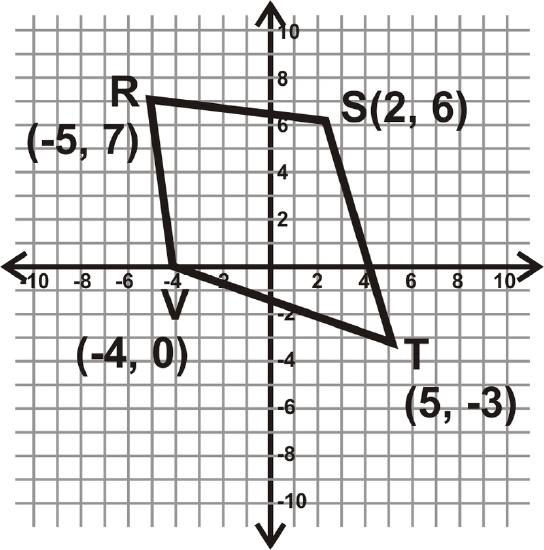
There are two directions you could take here. First, you could determine if the diagonals bisect each other. If they do, then it is a parallelogram. Or, you could find the lengths of all the sides. Let’s do this option.
\(\begin{aligned}
R S &=\sqrt{(-5-2)^{2}+(7-6)^{2}} & S T &=\sqrt{(2-5)^{2}+(6-(-3))^{2}} \\
&=\sqrt{(-7)^{2}+1^{2}} & &=\sqrt{(-3)^{2}+9^{2}} \\
&=\sqrt{50}=5 \sqrt{2} & &=\sqrt{90}=3 \sqrt{10} \\
R V=& \sqrt{(-5-(-4))^{2}+(7-0)^{2}} & V T &=\sqrt{(-4-5)^{2}+(0-(-3))^{2}} \\
=& \sqrt{(-1)^{2}+7^{2}} & &=\sqrt{(-9)^{2}+3^{2}} \\
=& \sqrt{50}=5 \sqrt{2} & &=\sqrt{90}=3 \sqrt{10}
\end{aligned}\)
From this we see that the adjacent sides are congruent. Therefore, \(RSTV\)is a kite.
Interactive Element
Add interactive element text here. This box will NOT print up in pdfs
Algebra Review: When asked to “simplify the radical,” pull all square numbers (1, 4, 9, 16, 25, ...) out of the radical. Above \(\sqrt{50}=\sqrt{25\cdot 2}\). We know \(\sqrt{25}=5\), so \(\sqrt{50}=\sqrt{25\cdot 2}=5\sqrt{2}\).
Recognizing Parallelograms
Is the quadrilateral \(ABCD\) a parallelogram?
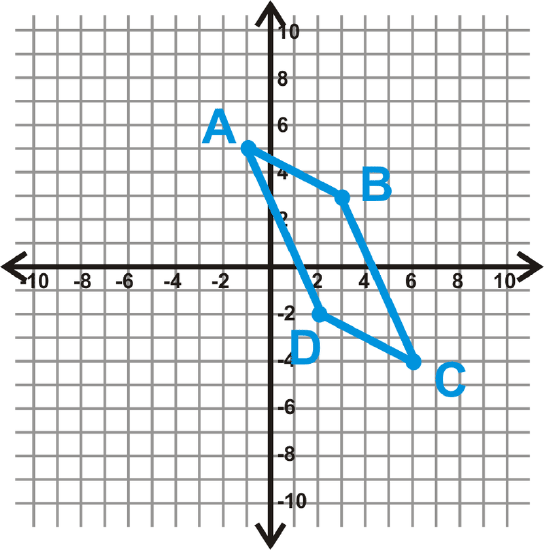
We have determined there are four different ways to show a quadrilateral is a parallelogram in the \(x−y\) plane. Let's check if a pair of opposite sides are congruent and parallel. First, find the length of \(AB\) and \(CD\).
\(\begin{aligned}
A B &=\sqrt{(-1-3)^{2}+(5-3)^{2}} & C D &=\sqrt{(2-6)^{2}+(-2+4)^{2}} \\
&=\sqrt{(-4)^{2}+2^{2}} & &=\sqrt{(-4)^{2}+2^{2}} \\
&=\sqrt{16+4} & &=\sqrt{16+4} \\
&=\sqrt{20} & &=\sqrt{20}
\end{aligned}\)
\(AB=CD\), so if the two lines have the same slope, \(ABCD\) is a parallelogram.
\(\text { Slope } A B=\dfrac{5-3}{-1-3}=\dfrac{2}{-4}=-\dfrac{1}{2} \text { Slope } C D=\dfrac{-2+4}{2-6}=\dfrac{2}{-4}=-\dfrac{1}{2}\)
Therefore, \(ABCD\) is a parallelogram.
Example \(\PageIndex{1}\)
A quadrilateral is defined by the four lines \(y=2x+1\), \(y=−2x+5\), \(y=2x−4\), and \(y=−2x−5\). Is this quadrilateral a rectangle?
Solution
To be a rectangle a shape must have four right angles. This means that the sides must be perpendicular to each other. From the given equations we see that the slopes are 2,−2, 2, and −2. Because the slopes are not opposite reciprocals of each other, the sides are not perpendicular, and the shape is not a rectangle.
Example \(\PageIndex{2}\)
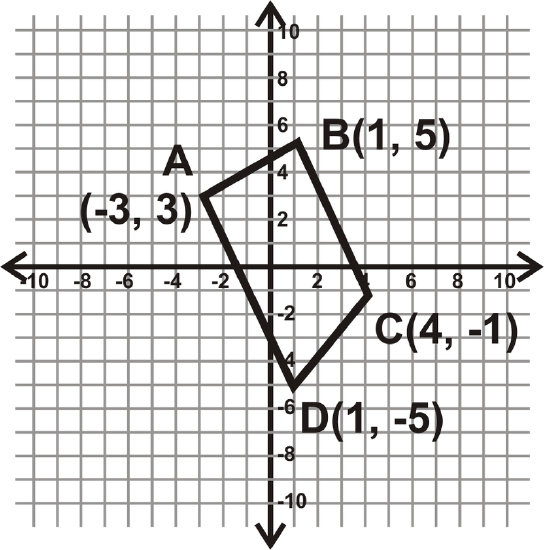
Determine what type of quadrilateral \(ABCD\) is. \(A(−3,3),\: B(1,5),\: C(4,−1),\: D(1,−5)\). Simplify all radicals.
Solution
First, graph \(ABCD\). This will make it easier to figure out what type of quadrilateral it is. From the graph, we can tell this is not a parallelogram. Find the slope of \overline{BC} and \overline{AD} to see if they are parallel.
\(\begin{array}{l}
\text { Slope of } \overline{B C}=\dfrac{5-(-1)}{1-4}=\dfrac{6}{-3}=-2 \\
\text { Slope of } \overline{A D}=\dfrac{3-(-5)}{-3-1}=\dfrac{8}{-4}=-2
\end{array}\)
We now know \(\overline{BC} \parallel \overline{AD}\). This is a trapezoid. To determine if it is an isosceles trapezoid, find \(AB\) and \(CD\).
\(\begin{aligned}
A B &=\sqrt{(-3-1)^{2}+(3-5)^{2}} & S T &=\sqrt{(4-1)^{2}+(-1-(-5))^{2}} \\
&=\sqrt{(-4)^{2}+(-2)^{2}} & &=\sqrt{3^{2}+4^{2}} \\
&=\sqrt{20}=2 \sqrt{5} & &=\sqrt{25}=5
\end{aligned}\)
\(AB\neq CD\), therefore this is only a trapezoid.
Example \(\PageIndex{3}\)
Determine what type of quadrilateral \(EFGH\) is. \(E(5,−1),\: F(11,−3),\: G(5,−5),\: H(−1,−3)\)
Solution
We will not graph this example. Let’s find the length of all four sides.
\(\begin{aligned}
E F &=\sqrt{(5-11)^{2}+(-1-(-3))^{2}} & F G &=\sqrt{(11-5)^{2}+(-3-(-5))^{2}} \\
&=\sqrt{(-6)^{2}+2^{2}} &=& \sqrt{6^{2}+2^{2}} \\
&=\sqrt{40}=2 \sqrt{10} & &=\sqrt{40}=2 \sqrt{10} \\
G H &=\sqrt{(5-(-1))^{2}+(-5-(-3))^{2}} & H &=\sqrt{(-1-5)^{2}+(-3-(-1))^{2}} \\
&=\sqrt{6^{2}+(-2)^{2}} & &=\sqrt{(-6)^{2}+(-2)^{2}} \\
=& \sqrt{40}=2 \sqrt{10} & &=\sqrt{40}=2 \sqrt{10}
\end{aligned}\)
All four sides are equal. That means, this quadrilateral is either a rhombus or a square. The difference between the two is that a square has four 90∘ angles and congruent diagonals. Let’s find the length of the diagonals.
\(\begin{aligned}
E G &=\sqrt{(5-5)^{2}+(-1-(-5))^{2}} & F H &=\sqrt{(11-(-1))^{2}+(-3-(-3))^{2}} \\
&=\sqrt{0^{2}+4^{2}} & &=\sqrt{12^{2}+0^{2}} \\
&=\sqrt{16}=4 & &=\sqrt{144}=12
\end{aligned}\)
The diagonals are not congruent, so \(EFGH\) is a rhombus.
Review
- If a quadrilateral has exactly one pair of parallel sides, what type of quadrilateral is it?
- If a quadrilateral has two pairs of parallel sides and one right angle, what type of quadrilateral is it?
- If a quadrilateral has perpendicular diagonals, what type of quadrilateral is it?
- If a quadrilateral has diagonals that are perpendicular and congruent, what type of quadrilateral is it?
- If a quadrilateral has four congruent sides and one right angle, what type of quadrilateral is it?
Determine what type of quadrilateral \(ABCD\) is.
- \(A(−2,4),\: B(−1,2),\: C(−3,1),\: D(−4,3)\)
- \(A(−2,3),\: B(3,4),\: C(2,−1),\: D(−3,−2)\)
- \(A(1,−1),\: B(7,1),\: C(8,−2),\: D(2,−4)\)
- \(A(10,4),\: B(8,−2),\: C(2,2),\: D(4,8)\)
- \(A(0,0),\: B(5,0),\: C(0,4),\: D(5,4)\)
- \(A(−1,0),\: B(0,1),\: C(1,0),\: D(0,−1)\)
- \(A(2,0),\: B(3,5),\: C(5,0),\: D(6,5)\)
SRUE is a rectangle and PRUC is a square.
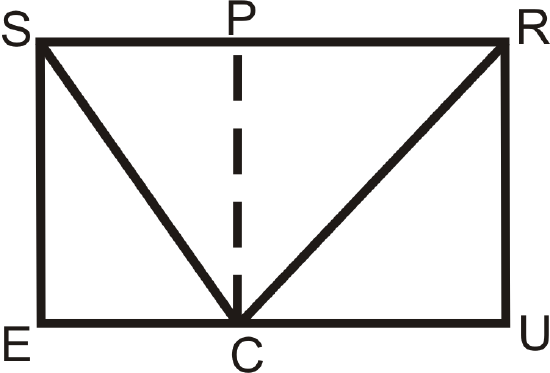
- What type of quadrilateral is \(SPCE\)?
- If \(SR=20\) and \(RU=12\), find \(CE\).
- Find SC and RC based on the information from part b. Round your answers to the nearest hundredth.
Review (Answers)
To view the Review answers, open this PDF file and look for section 6.8.
Vocabulary
| Term | Definition |
|---|---|
| Kite | A kite is a quadrilateral with distinct adjacent congruent sides. |
| Parallelogram | A parallelogram is a quadrilateral with two pairs of parallel sides. |
| Quadrilateral | A quadrilateral is a closed figure with four sides and four vertices. |
| Rectangle | A rectangle is a quadrilateral with four right angles. |
| Rhombus | A rhombus is a quadrilateral with four congruent sides. |
| Trapezoid | A trapezoid is a quadrilateral with exactly one pair of parallel opposite sides. |

