6.16: Angles On and Inside a Circle
- Page ID
- 5041
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Angles whose vertices are on the circumference of a circle or formed by tangent lines and chords.
When we say an angle is on a circle, we mean the vertex is on the edge of the circle. One type of angle on a circle is the inscribed angle (see Inscribed Angles in Circles). Another type of angle on a circle is one formed by a tangent and a chord.
Chord/Tangent Angle Theorem: The measure of an angle formed by a chord and a tangent that intersect on a circle is half the measure of the intercepted arc.
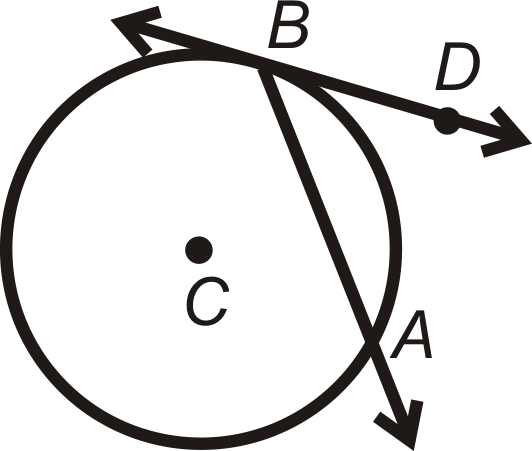
\(m\angle DBA=\dfrac{1}{2}m\widehat{AB}\)
If two angles, with their vertices on the circle, intercept the same arc then the angles are congruent.
An angle is inside a circle when the vertex lies anywhere inside the circle.
Intersecting Chords Angle Theorem: The measure of the angle formed by two chords that intersect inside a circle is the average of the measures of the intercepted arcs.
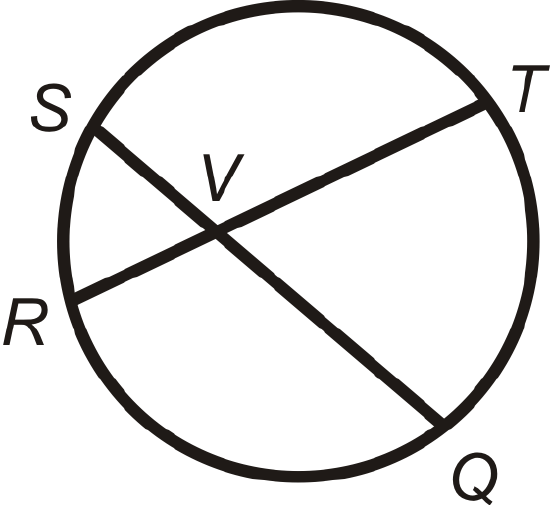
\(\begin{aligned}m\angle SVR&=\dfrac{1}{2}(m\widehat{SR} +m\widehat{TQ} )=m\widehat{SR} +m\widehat{TQ} 2=m\angle TVQ \\ m\angle SVT&=\dfrac{1}{2}(m\widehat{ST} +m\widehat{RQ} )=m\widehat{ST} +m\widehat{RQ} 2=m\angle RVQ\end{aligned}\)
What if you were given a circle with either a chord and a tangent or two chords that meet at a common point? How could you use the measure of the arc(s) formed by those circle parts to find the measure of the angles they make on or inside the circle?
Example \(\PageIndex{1}\)
Find \(x\).
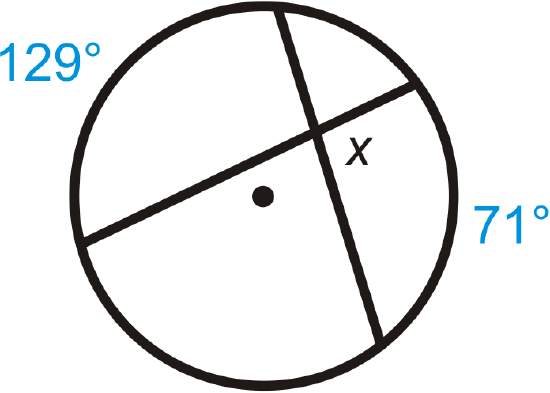
Solution
Use the Intersecting Chords Angle Theorem to write an equation.
\(x=\dfrac{129^{\circ}+71^{\circ}}{2}=\dfrac{200^{\circ}}{2}=100^{\circ}\)
Example \(\PageIndex{2}\)
Find \(x\).
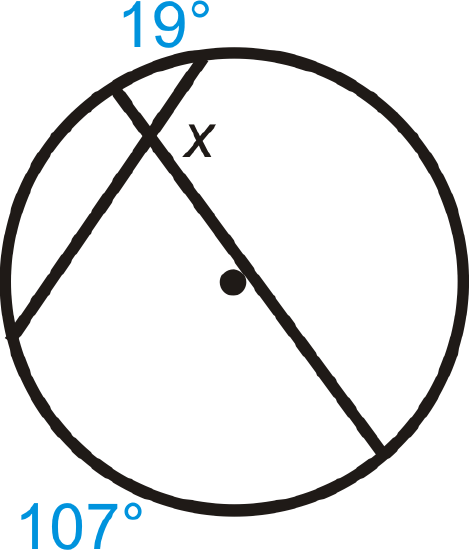
Solution
Use the Intersecting Chords Angle Theorem to write an equation.
\(x\) is supplementary to the angle that is the average of the given intercepted arcs. We call this supplementary angle \(y\).
\(y=\dfrac{19^{\circ}+107^{\circ}}{2}=\dfrac{126^{\circ}}{2}=63^{\circ} \qquad x+63^{\circ}=180^{\circ}; \: x=117^{\circ}\)
Example \(\PageIndex{3}\)
Find \(m\angle BAD\).
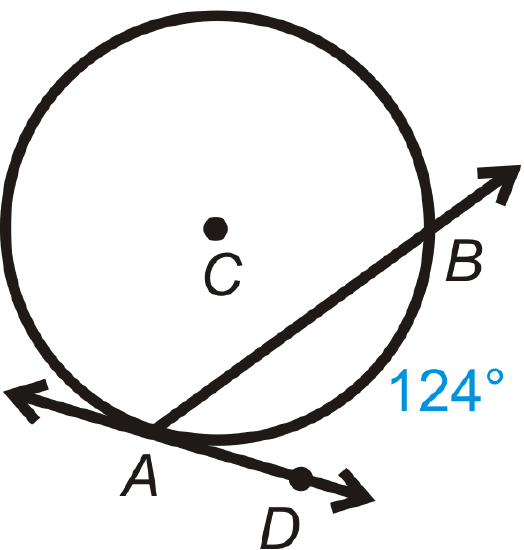
Solution
Use the Chord/Tangent Angle Theorem. \(m\angle BAD=\dfrac{1}{2}m\widehat{AB}=\dfrac{1}{2}\cdot 124^{\circ}=62^{\circ}\).
Example \(\PageIndex{4}\)
Find \(a\), \(b\), and \(c\).
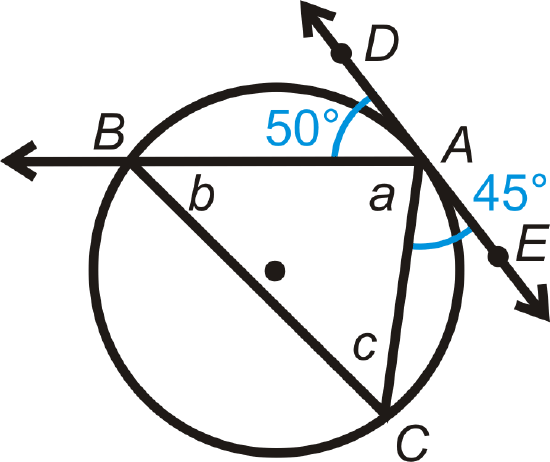
Solution
\(\begin{array}{c}
50^{\circ}+45^{\circ}+m \angle a=180^{\circ} \quad \text { straight angle } \\
m \angle a=85^{\circ} \\
m \angle b=\frac{1}{2} \cdot m \widehat{A C} \\
\qquad \begin{array}{c}
\widehat{A C}=2 \cdot m \angle E A C=2 \cdot 45^{\circ}=90^{\circ} \\
m \angle b=\frac{1}{2} \cdot 90^{\circ}=45^{\circ}
\end{array} \\
85^{\circ}+45^{\circ}+m \angle c=180^{\circ} \quad \text { Triangle Sum Theorem } \\
m \angle c=50^{\circ}
\end{array}\)
Example \(\PageIndex{5}\)
Find \(m\widehat{AEB}\).
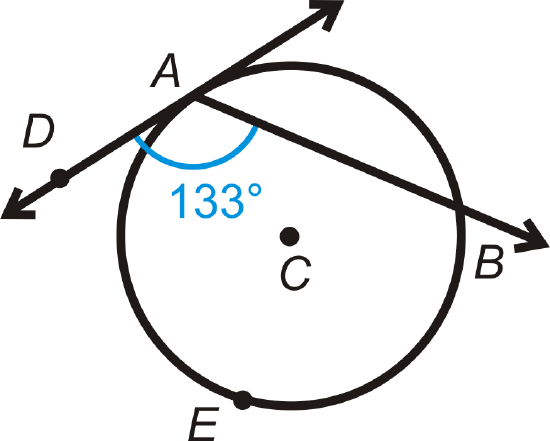
Solution
Use the Chord/Tangent Angle Theorem. \(m\widehat{AEB}=2\cdot m\angle DAB=2\cdot 133^{\circ}=266^{\circ}.\)
Review
Find the value of the missing variable(s).
-
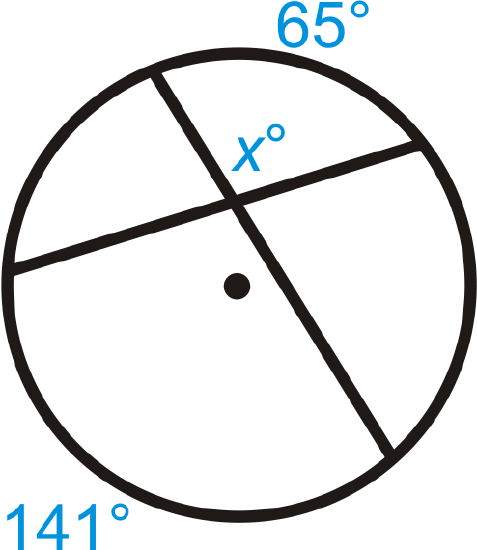
Figure \(\PageIndex{8}\) -
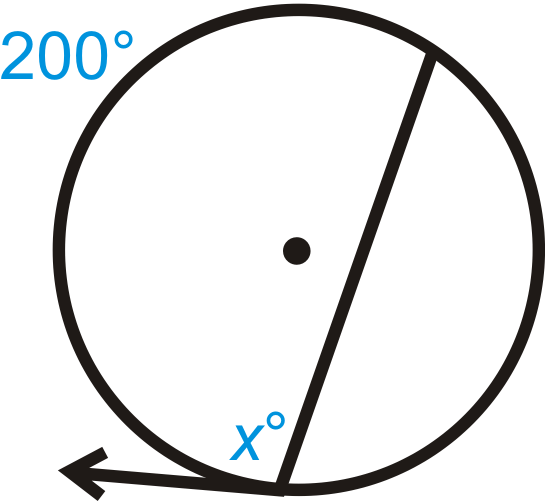
Figure \(\PageIndex{9}\) -
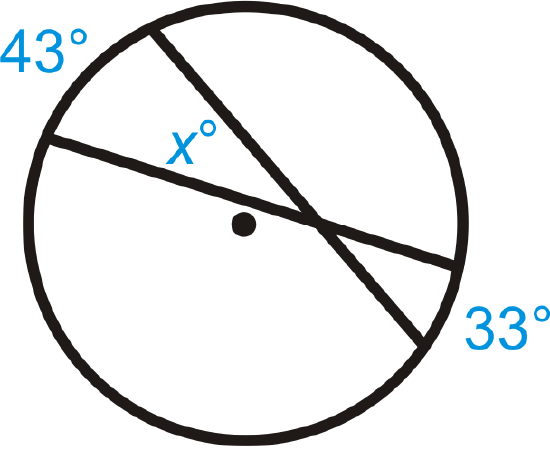
Figure \(\PageIndex{10}\) -
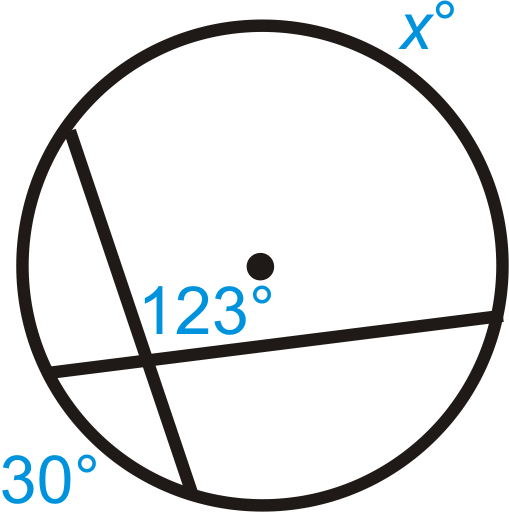
Figure \(\PageIndex{11}\) -
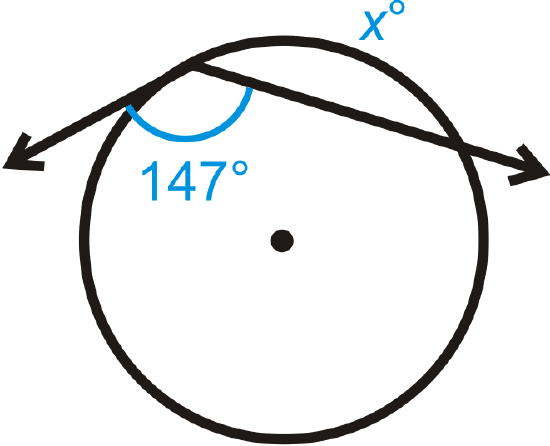
Figure \(\PageIndex{112}\) -
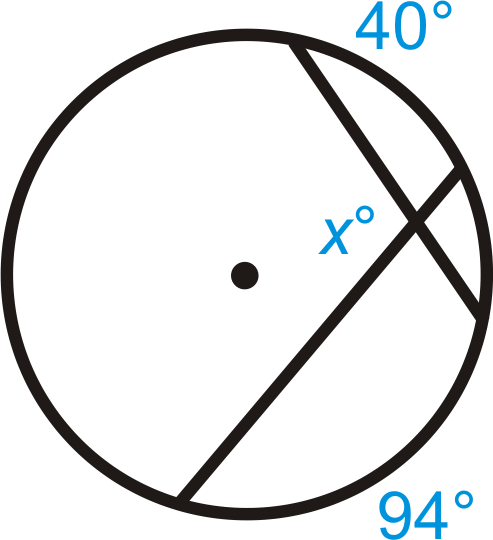
Figure \(\PageIndex{13}\) - \(y\neq 60^{\circ}\)
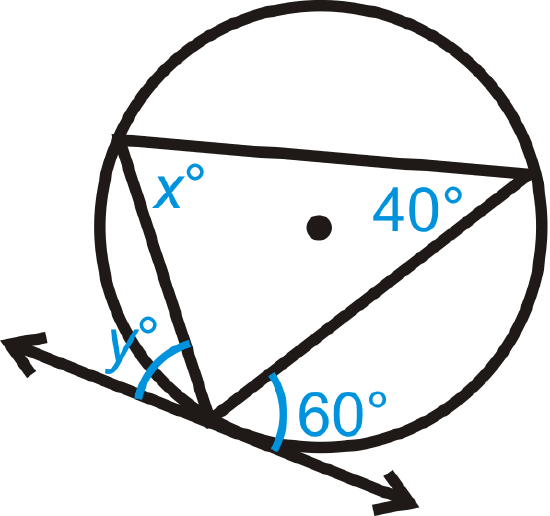
Figure \(\PageIndex{14}\)
Solve for \(x\).
- Fill in the blanks of the proof for the Intersecting Chords Angle Theorem
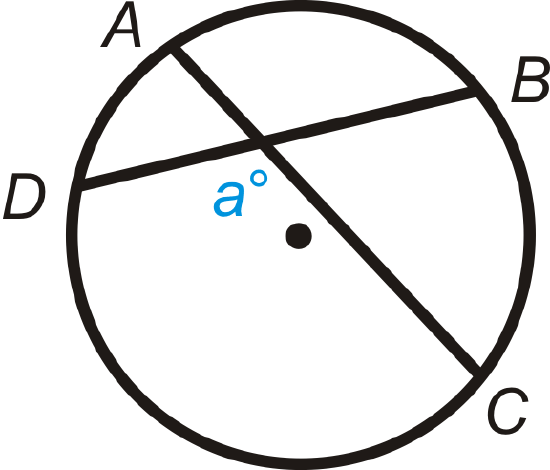
Figure \(\PageIndex{15}\)
Given: Intersecting chords \(\overline{AC}\) and \(\overline{BD}\).
Prove: \(m\angle a=\dfrac{1}{2}(m\widehat{DC}+m\widehat{AB})\)
| Statement | Reason |
|---|---|
| 1. Intersecting chords \(\overline{AC}\) and \(\overline{BD}\). | 1. |
|
2. Draw \(\overline{BC}\) 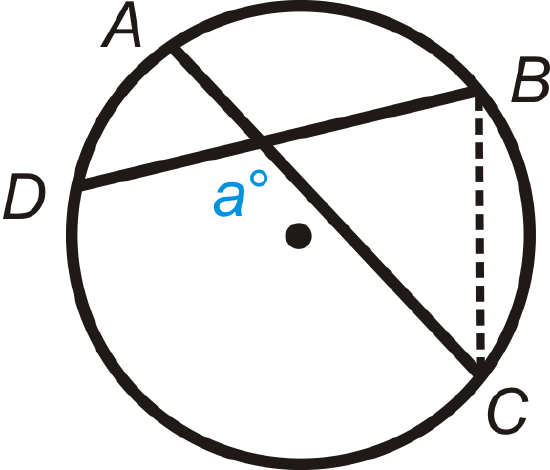
|
2. Construction |
|
3. \(m\angle DBC=\dfrac{1}{2}m\widehat{DC}\) \(m\angle ACB=\dfrac{1}{2}m\widehat{AB}\) |
3. |
| 4. \(m\angle a=m\angle DBC+m\angle ACB\) | 4. |
| 5. \(m\angle a=\dfrac{1}{2}m\widehat{DC}+\dfrac{1}{2}m\widehat{AB}\) | 5. |
Fill in the blanks.
- If the vertex of an angle is _______________ a circle, then its measure is the average of the __________________ arcs.
- If the vertex of an angle is ________ a circle, then its measure is ______________ the intercepted arc.
Vocabulary
| Term | Definition |
|---|---|
| central angle | An angle formed by two radii and whose vertex is at the center of the circle. |
| chord | A line segment whose endpoints are on a circle. |
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| inscribed angle | An angle with its vertex on the circle and whose sides are chords. |
| intercepted arc | The arc that is inside an inscribed angle and whose endpoints are on the angle. |
| point of tangency | The point where the tangent line touches the circle. |
| radius | The distance from the center to the outer rim of a circle. |
| Chord/Tangent Angle Theorem | The Chord/Tangent Angle Theorem states that the measure of an angle formed by a chord and a tangent that intersect on a circle is half the measure of the intercepted arc. |
| Intersecting Chords Angle Theorem | The Intersecting Chords Angle Theorem states that the measure of the angle formed by two chords that intersect inside a circle is the average of the measures of the intercepted arcs. |
Additional Resources
Interactive Element
Video: Angles On and Inside a Circle Principles - Basic
Activities: Angles On and Inside a Circle Discussion Questions
Study Aids: Arcs and Angles Study Guide
Practice: Angles On and Inside a Circle

