6.17: Angles Outside a Circle
- Page ID
- 5042
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Angles formed by tangents and/or secants.
An angle is outside a circle if its vertex is outside the circle and its sides are tangents or secants. The possibilities are: an angle formed by two tangents, an angle formed by a tangent and a secant, and an angle formed by two secants.
Outside Angle Theorem: The measure of an angle formed by two secants, two tangents, or a secant and a tangent from a point outside the circle is half the difference of the measures of the intercepted arcs.
\(m\angle D=\dfrac{m\widehat{EF}−m\widehat{GH}}{2}\), \(m\angle L=\dfrac{m\widehat{MPN}−m\widehat{MN}}{2}\), \(m\angle Q=\dfrac{m\widehat{RS}−m\widehat{RT}}{2}\)
What if you were given a circle with either two secants, two tangents, or one of each that share a common point outside the circle? How could you use the measure of the arcs formed by those circle parts to find the measure of the angle they make outside the circle?
Example \(\PageIndex{1}\)
Find the measure of \(x\).
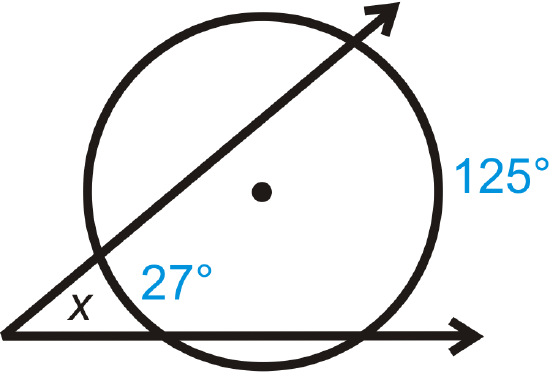
Solution
Use the Outside Angle Theorem.
\(x=\dfrac{125^{\circ} −27^{\circ}}{2}=\dfrac{98^{\circ}}{2}=49^{\circ}\)
Example \(\PageIndex{2}\)
Find the measure of \(x\).
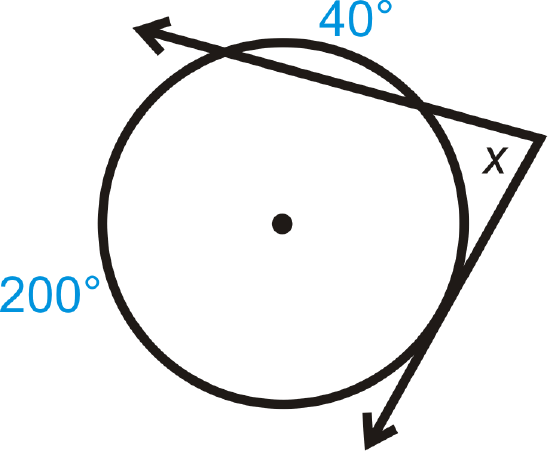
Solution
Use the Outside Angle Theorem.
\(40^{\circ}\) is not the intercepted arc. The intercepted arc is \(120^{\circ}\), \((360^{\circ} −200^{\circ} −40^{\circ})\). \(x=\dfrac{200^{\circ} −120^{\circ} }{2}=\dfrac{80^{\circ} }{2}=40^{\circ}\)
Example \(\PageIndex{3}\)
Find the value of \(x\).
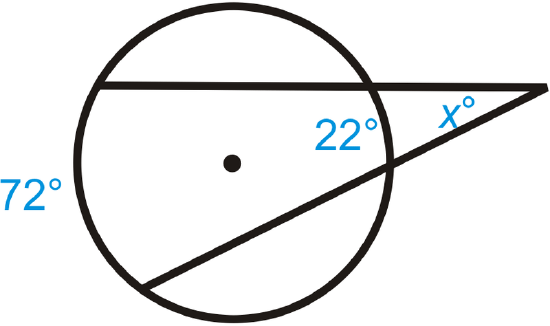
Solution
\(x=\dfrac{72^{\circ} −22^{\circ} }{2}=\dfrac{50^{\circ} }{2}=25^{\circ}\).
Example \(\PageIndex{4}\)
Find the value of \(x\).
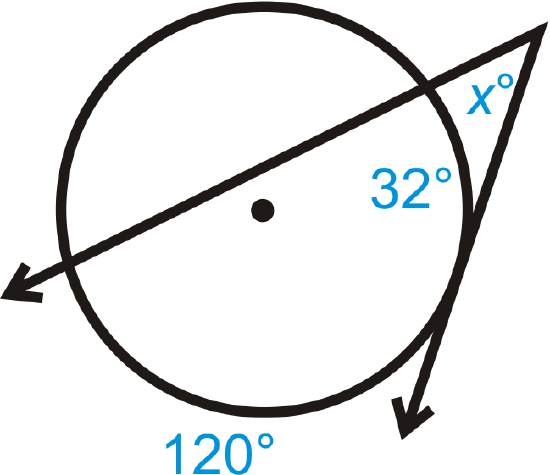
Solution
\(x=\dfrac{120^{\circ} −32^{\circ}}{2}=\dfrac{88^{\circ} }{2}=44^{\circ}\).
Example \(\PageIndex{5}\)
Find the value of \(x\).
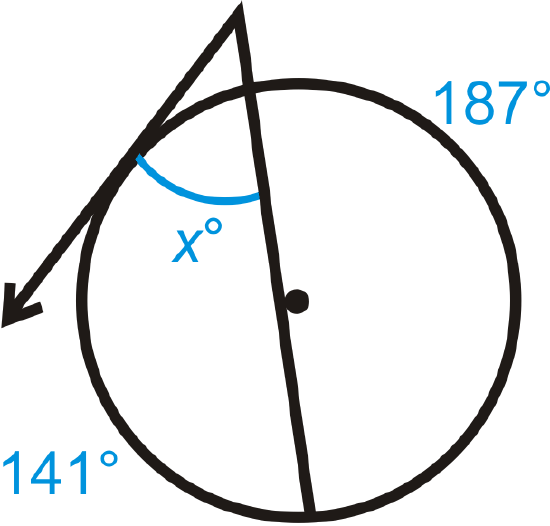
Solution
First note that the missing arc by angle \(x\) measures \(32^{\circ}\) because the complete circle must make \(360^{\circ}\). Then, \(x=\dfrac{141^{\circ} −32^{\circ}}{2}=\dfrac{109^{\circ}}{2}=54.5^{\circ}\).
Review
Find the value of the missing variable(s).
-
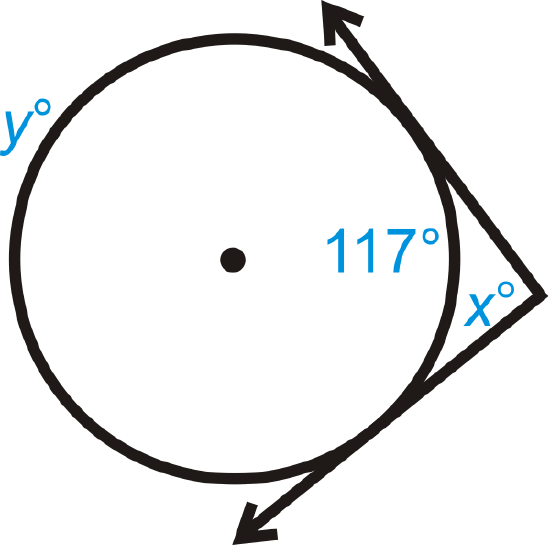
Figure \(\PageIndex{7}\) -
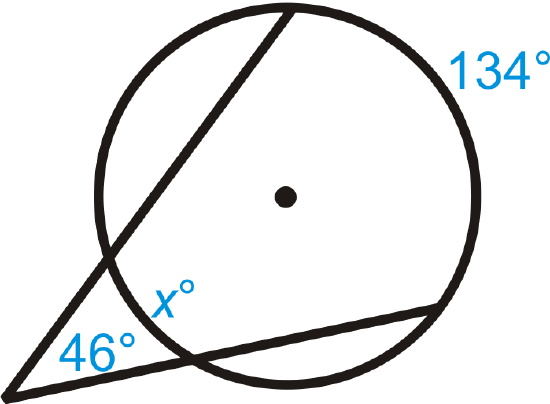
Figure \(\PageIndex{8}\) -
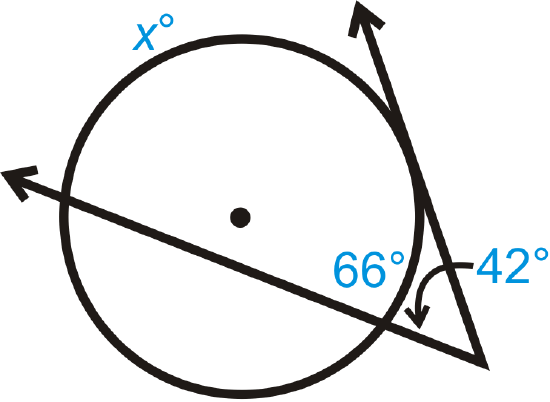
Figure \(\PageIndex{9}\) -
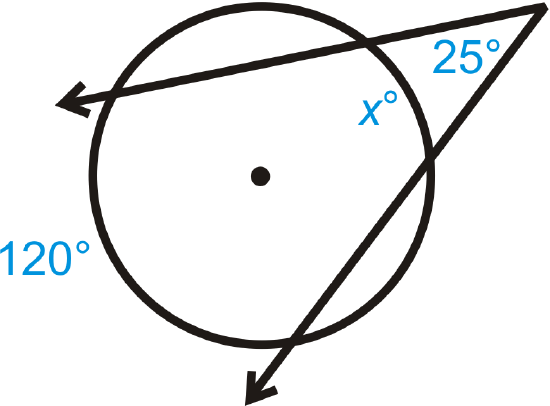
Figure \(\PageIndex{10}\) -
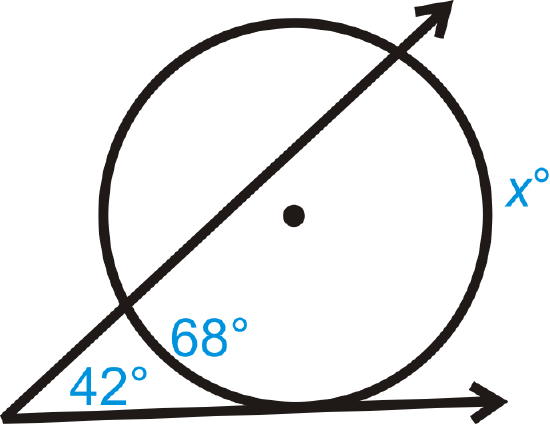
Figure \(\PageIndex{11}\) -
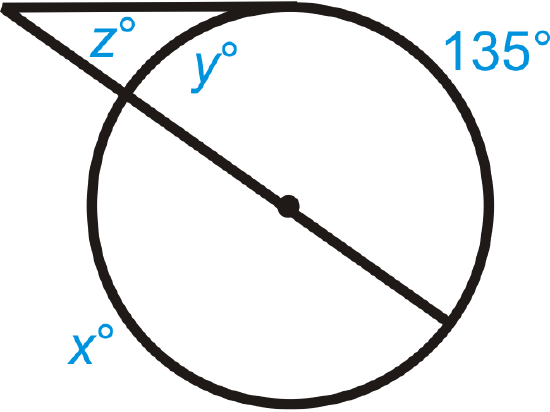
Figure \(\PageIndex{12}\) -
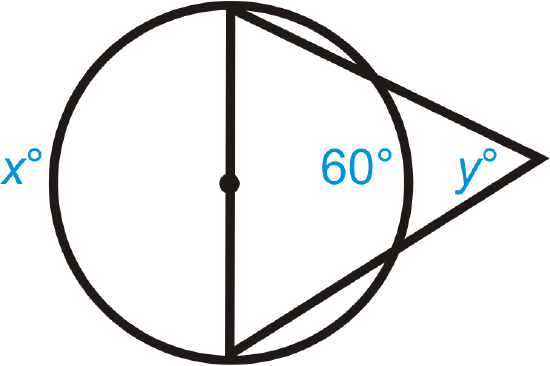
Figure \(\PageIndex{13}\)
Solve for \(x\).
-
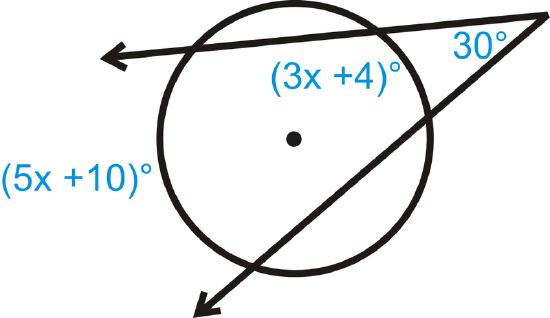
Figure \(\PageIndex{14}\) -
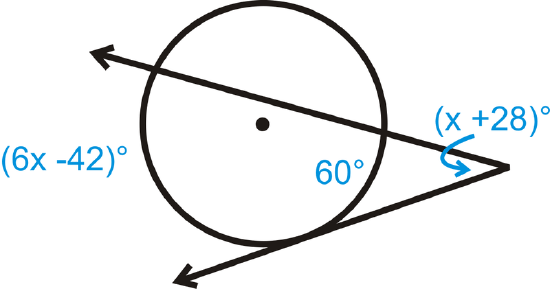
Figure \(\PageIndex{15}\) - Fill in the blanks of the proof for the Outside Angle Theorem
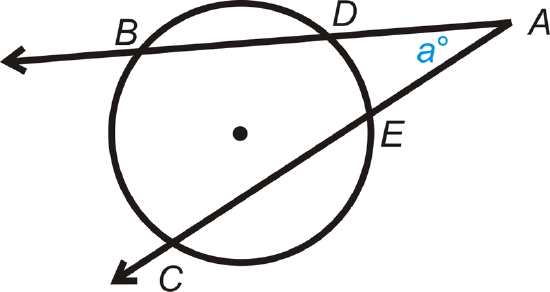
Given: Secant rays \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\)
Prove: \(m\angle a=12(m\widehat{BC}−m\widehat{DE})\)
| Statement | Reason |
|---|---|
| 1. Intersecting secants \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\). | 1. |
|
2. Draw \(\overline{BE}\).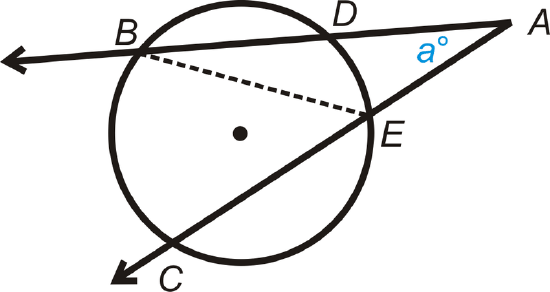 
|
2. Construction |
|
3. \(m\angle BEC=\dfrac{1}{2}m\widehat{BC}\) \(m\angle DBE=\dfrac{1}{2}m\widehat{DE}\) |
3. |
| 4. \(m\angle a+m\angle DBE=m\angle BEC\) | 4. |
| 5. | 5. Subtraction PoE |
| 6. | 6. Substitution |
| 7. \(m\angle a=\dfrac{1}{2}(m\widehat{BC}−m\widehat{DE})\) | 7. |
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.8.
Vocabulary
| Term | Definition |
|---|---|
| central angle | An angle formed by two radii and whose vertex is at the center of the circle. |
| chord | A line segment whose endpoints are on a circle. |
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| inscribed angle | An angle with its vertex on the circle and whose sides are chords. |
| intercepted arc | The arc that is inside an inscribed angle and whose endpoints are on the angle. |
| point of tangency | The point where the tangent line touches the circle. |
| radius | The distance from the center to the outer rim of a circle. |
| Secant | The secant of an angle in a right triangle is the value found by dividing length of the hypotenuse by the length of the side adjacent the given angle. The secant ratio is the reciprocal of the cosine ratio. |
| Tangent | The tangent of an angle in a right triangle is a value found by dividing the length of the side opposite the given angle by the length of the side adjacent to the given angle. |
| Outside Angles Theorem | The Outside Angles Theorem states that the measure of an angle formed by two secants, two tangents, or a secant and a tangent from a point outside the circle is half the difference of the measures of the intercepted arcs. |
Additional Resources
Interactive Element
Video: Angles Outside a Circle Principles - Basic
Activities: Angles Outside a Circle Discussion Questions
Study Aids: Arcs and Angles Study Guide
Practice: Angles Outside a Circle