8.1: Identify Transformation Types
- Page ID
- 2161
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify transformations, translations, reflections and rotations.
Transformations in the Plane
Transformation is a process that changes the shape, size or position of a figure to create a new image. It is a function that takes points in the plane as inputs and gives other points as outputs. You can think of a transformation as a rule that tells you how to create new points.
Suppose you have a transformation \(F\) that applies a horizontal stretch factor of two to each point. Below, this transformation is applied to triangle \(S\) to create triangle \(S'\).
- \(S'\) is considered the image of \(S\) by \(F\).
- It is also correct to say that \(F\) maps \(S\) to \(S'\).
- Each of the points in the image are labeled with a ′ symbol, which is read as "prime."
This helps to show how points on \(S\) correspond to points on \(S'\). For example, you could say that "point A maps to point A-prime."
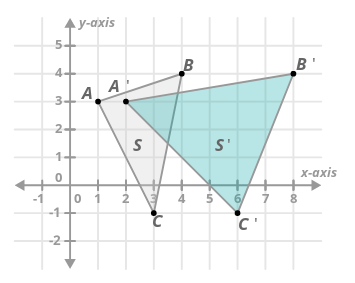
Some transformations preserve length and angles. Preserving length means that if a line segment is 3 units, its image will also be 3 units. Similarly, preserving angles means if an angle is \(60^{\circ}\), its image will also be \(60^{\circ}\).
- A transformation that preserves length and angles is called a rigid transformation.
Recognizing Rigid Transformations
- Is a horizontal stretch an example of a rigid transformation?
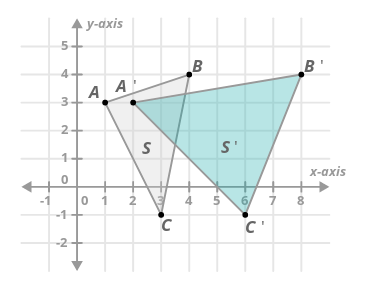
No. You can prove this using the picture above by showing that length is not preserved.
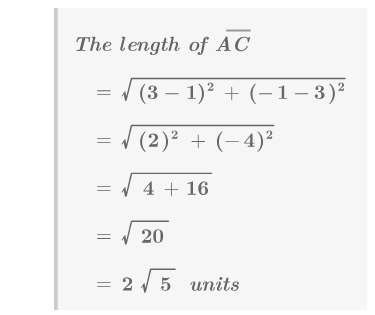
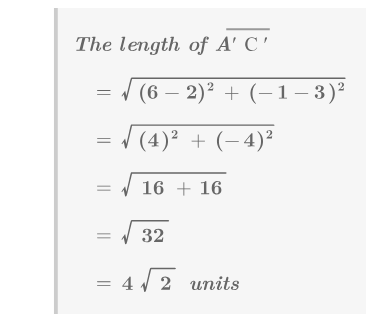
- A transformation reflects points in shape \(K\) across \(\overleftrightarrow{AB}\) to create shape \(K′\). Is this reflection a rigid transformation?
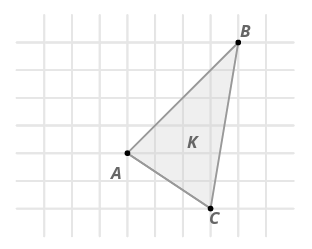
Yes, reflections are rigid transformations. You can verify that the distances between the points are preserved.
- A transformation translates points in shape \(K\) along vector \(\rightarrow{v}\) to create shape \(K′\). Is this translation a rigid transformation?
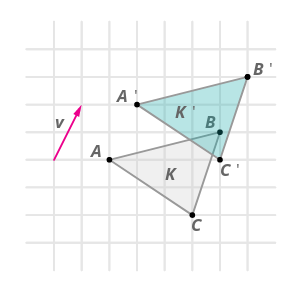
Yes, translations are rigid transformations. You can verify that the distances between the points are preserved.
Interactive Element
Add interactive element text here. This box will NOT print up in pdfs
Example \(\PageIndex{1}\)
You slide a book across your desk. You pour soda from a can into a big glass. Describe these actions as transformations.
Solution
Sliding a book across your desk is a rigid transformation because a book is a rigid object that does not change shape. The distances and angles that make up the book don't change once the book is in a new location. Pouring soda, on the other hand, is not a rigid transformation. Liquid is not a rigid object and it can change shape depending on its surroundings. The overall shape of the soda in the can will be different from the overall shape of the soda in the glass.
Example \(\PageIndex{2}\)
A transformation rotates points in shape \(K\) around point \(D\) to create shape \(K′\). Does this rotation look like a rigid transformation? Use algebra to prove your answer.
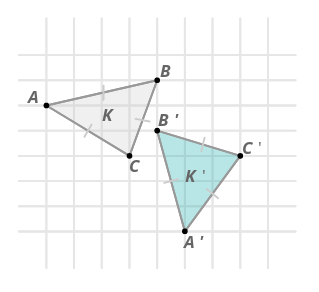
Solution
This appears to be a rigid transformation.
With the Pythagorean Theorem, you can show that the corresponding sides are the same length. For example:
\(\begin{aligned} \text{ The length of } \overline{AC} \\&=\sqrt{3^2+2^2} \\ &=\sqrt{9+4} \\ &=\sqrt{13}\text{ units } \\ \text{ The length of }\overline{A′C′} \\ &=\sqrt{3^2+2^2} \\ &=\sqrt{9+4} \\ &=\sqrt{13}\text{ units } \end{aligned}\)
Thus it is indeed a rigid transformation.
Example \(\PageIndex{3}\)
What makes a transformation a rigid transformation?
Solution
Rigid transformations preserve distance and angles. All corresponding sides will be the same length and all corresponding angles will be the same measure.
Review
For 1-7, define each statement as true or false and justify your answer.
1. Translations are rigid transformations.
2. Rotations are rigid transformations.
3. Horizontal stretches are rigid transformations.
4. Rigid transformations preserve location in the plane.
5. Corresponding sides in rigid transformations are the same length.
6. If it's not a rigid transformation, it's not a real transformation.
7. Reflections are rigid transformations.
Use the following image for 8-9.
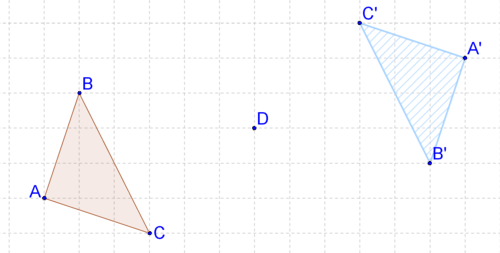
8. Describe the transformation in your own words. Does it look like a rigid transformation?
9. Prove your answer to #8 by comparing the lengths of two sides.
Use the following image for 10-11.
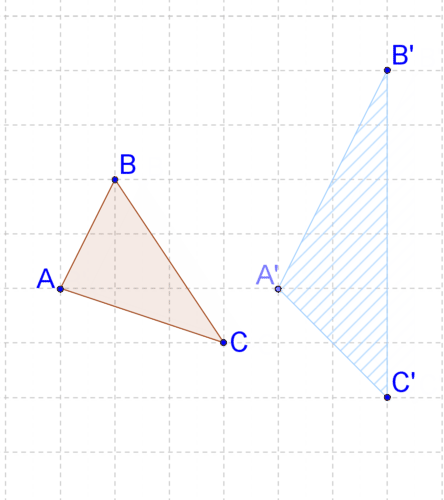
10. Describe the transformation in your own words. Does it look like a rigid transformation?
11. Prove your answer to #10 by comparing the lengths of two sides.
Use the following image for 12-13.
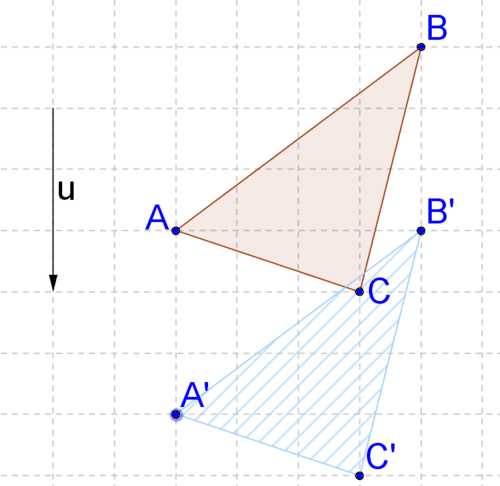
12. Describe the transformation in your own words. Does it look like a rigid transformation?
13. Prove your answer to #12 by comparing the lengths of two sides.
Use the following image for 14-15.
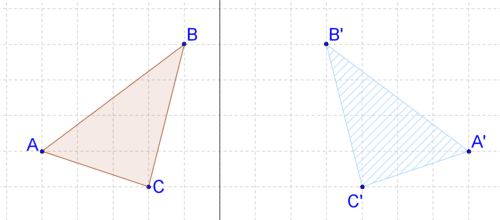
14. Describe the transformation in your own words. Does it look like a rigid transformation?
15. Prove your answer to #14 by comparing the lengths of two sides.
16. A transformation can be thought of as a movement of an object in a plane such that angle measures and segment lengths are preserved. Imagine a triangle that you've cut out, lying flat on a piece of poster paper. How can the triangle be moved so that the measures of angles and the lengths of segments are preserved? How can the different types of movements be categorized and defined? Be creative. Draw, write, and discuss how to more specifically describe and define the types and methods of rigid motion transformations.
17. There is one type of rigid motion transformation which seems to require the triangle described above to be lifted from the poster board and flipped. (Mathematically, that's not what happens, but it looks that way from our 3-dimensional perspective.) How can this transformation be defined and described?
18. Sometimes we can describe transformations in the coordinate plane. For example, one can specifically alter the coordinates of the vertices of a polygon according to a rule. Think about how you can modify the coordinates of a point and what the consequences of each type of modification would be. Experiment. Draw a polygon on a coordinate plane, and alter the coordinates according to different rules, then draw the resulting images. Write about and discuss your conclusions.
19. Define and describe the transformations that map \(A\) to \(A'\) to \(A''\) to \(A'''\) below.
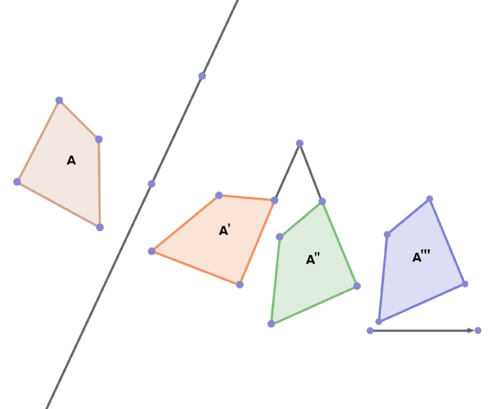
20. Some of the images below represent rigid motion transformations of polygon B and some do not. Decide which do and which don't, and explain your choices. Define and describe the ones that do.
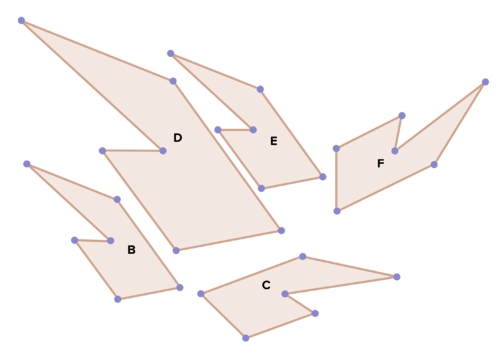
Review (Answers)
To see the Review answers, click here.
Additional Resources
Interactive Element
Practice: Identify Transformation Types

