8.2: Lines of Symmetry
- Page ID
- 2162
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify existence and number of lines of symmetry.
Identify Lines of Symmetry

Symmetry is the key to the balance of a design or structure.
What is symmetry? How does an image have symmetry? What would you have to do to be sure that an image or construction was symmetrical?
In this concept, you will learn to identify lines of symmetry.
Symmetry
Sometimes, a figure will have parts that mirror themselves within one object. In this case, parts of the object match other parts of the picture. This is called symmetry.
Let’s look at an example.

Look at this heart. It has two sides that match. The heart is symmetrical because there is symmetry in its design. This heart can be divided in half vertically where one half matches the other half.

This line that divides the heart into matching parts is called the line of symmetry.
You can determine other lines of symmetry by looking at other objects.
Let’s look at another example.

Look at this cross. It has two lines of symmetry. If you look, the cross can be divided in half perfectly vertically and in half horizontally.
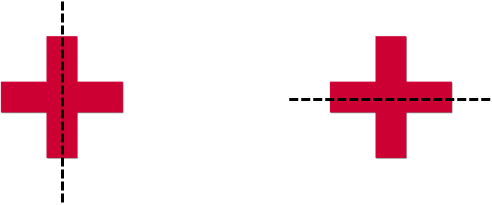
This means that there are two lines of symmetry in the cross.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about questions on symmetry.
- What is symmetry?
- How does an image have symmetry?
- What would you have to do to be sure that your image was symmetrical?
Solution
- Symmetry is when two halves of an object match. In other words, you can divide the object into parts and the parts are congruent. A heart is a symmetrical object, so is the letter A.
- An image has symmetry because it can be divided in half so that one half of the image matches the other half.
- For an image to have a line of symmetry the image must be able to fold alone the line of symmetry so that the two parts are mirror images of each other. The folded line would be the line of symmetry. An image that is symmetrical would have a line of symmetry such as a square (four lines of symmetry), a circle (infinite lines of symmetry) or a butterfly (one line of symmetry).
Example \(\PageIndex{2}\)
Does this figure have symmetry? Can it be a reflection?

Solution
First, try to divide this butterfly evenly so that one side can reflect the other. Can you draw a line of symmetry?

The answer is yes.
Therefore, it has symmetry.
Example \(\PageIndex{3}\)
Does the figure below have symmetry? Can it be a reflection?

Solution
First, try to divide this flower evenly so that one side can reflect the other. Can you draw a line of symmetry?

The answer is yes.
Therefore, it has symmetry.
Example \(\PageIndex{4}\)
How many lines of symmetry does this figure have?

Solution
First, try to divide this rectangle evenly so that one side can reflect the other. Can you draw a line of symmetry?

The answer is yes. Therefore, a rectangle has two lines of symmetry.
Example \(\PageIndex{5}\)
Do these figures have symmetry?

Solution
First, try to divide these images evenly so that one side can reflect the other. Can you draw a line of symmetry for any of these images?
The answer is no.
Therefore, none of these images have a line of symmetry.
Review
Use the illustration to answer each question.
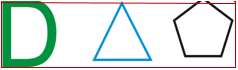
1. Do these figures have symmetry?
2. Can they be reflections?
3. How many lines of symmetry does each figure have?
Find all lines of symmetry for the shapes below.
-
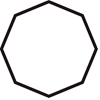
Figure \(\PageIndex{14}\) -

Figure \(\PageIndex{15}\) -
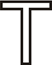
Figure \(\PageIndex{16}\)
Name the number of lines of symmetry for each letter.
-

Figure \(\PageIndex{17}\) -

Figure \(\PageIndex{18}\) -

Figure \(\PageIndex{19}\) -

Figure \(\PageIndex{20}\) -

Figure \(\PageIndex{21}\)
Answer each question true or false.
12. All triangles have symmetry.
13. All circles have symmetry.
14. The letter “\(x\)” has two lines of symmetry.
15. The letter “\(s\)” has two lines of symmetry.
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.13.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Lines of Symmetry | Lines of symmetry are the lines that can be drawn to divide a figure into equal halves. |
| Reflection | A reflection is a transformation that flips a figure on the coordinate plane across a given line without changing the shape or size of the figure. |
| Symmetry | A figure has symmetry if it can be transformed and still look the same. |
Additional Resources
Video: Rotational Symmetry Tutorial
Practice: Lines of Symmetry
Real World: The Balance of Nature

