8.6: Sliding Figures
- Page ID
- 2165
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Use coordinates to move figures on the coordinate plane.
Transformation Classification

Mrs. Gilcrest has designed a special version of the game Battleship. Her version requires students to use coordinates such as (1, 2) to guess the location of a ship. The ships are strategically placed so that each is a translation of the other. In order to keep the game easier for the students, she translated the ships the same distance up or down, right or left. If the first ship is at (3, 6), (3, 7), (3, 8) and the second ship is translated 4 units to the right and 4 units up, what are the coordinates of the second ship?
In this concept, you will learn how to classify transformations.
Classifying Transformations
The coordinate plane is a representation of two-dimensional space. It has a horizontal axis, called the \(x\)-axis, and a vertical axis, called the \(y\)-axis. You can graph and move geometric figures on the coordinate plane.
Remember the three types of transformations: translation, reflection and rotation.
Now let’s look at performing each type of transformation in the coordinate plane.
When you perform translations, you slide a figure left or right, up or down. This means that on the coordinate plane, the coordinates for the vertices of the figure will change. Take a look at the example below.
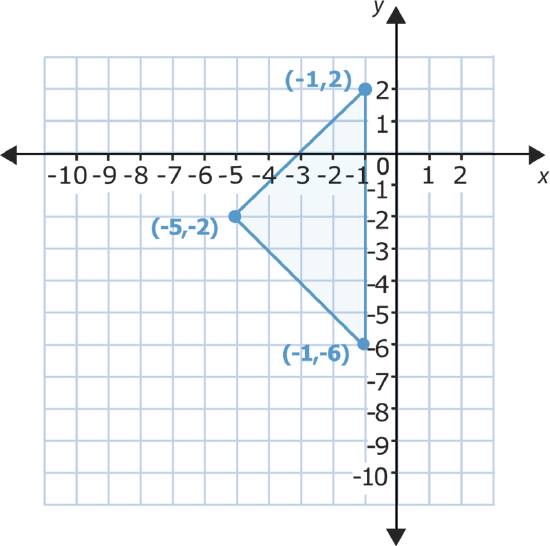
Now let’s look at performing a translation or slide of this figure.
You can choose the number of places that you want to move the triangle and the direction that you wish to move it in. If you slide this triangle 3 places down, all of its vertices will shift 3 places down the \(y\)-axis and the \(y\)-coordinate in each pair will decrease by 3.
Let’s see why this happens.
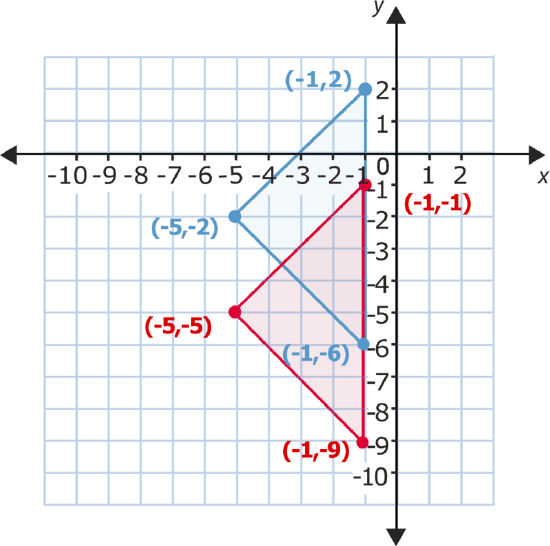
You can see the change in all of the \(y\)-coordinates. Compare the top points. The \(y\)-coordinate on the left is 2. The \(y\)-coordinate for the corresponding point in the triangle after it moves is -1. The \(y\)-coordinate decreases by 3. Now compare the left-hand point of each triangle. The \(y\)-coordinate originally is -2, and the \(y\)-coordinate after the translation is -5. Again, the difference shows a change of -3 in the \(y\)-coordinate. For the last point, the \(y\)-coordinate starts out as -6, and shifts to -9 after the downward slide. For each point, the \(y\)-coordinate decreases by 3 while the \(x\)-coordinates stay the same.
You can translate figures in other ways, too. As you might guess, you move figures right or left on the coordinate grid by their \(x\)-coordinates. You can also move figures diagonally by changing both their x and \(y\)-coordinates. One way to recognize translations, then, is to compare their points. The \(x\)-coordinates will all change the same way, and the \(y\)-coordinates will all change the same way.
Here is an example of how to graph a translation.
Slide the following figure 5 places to the right.
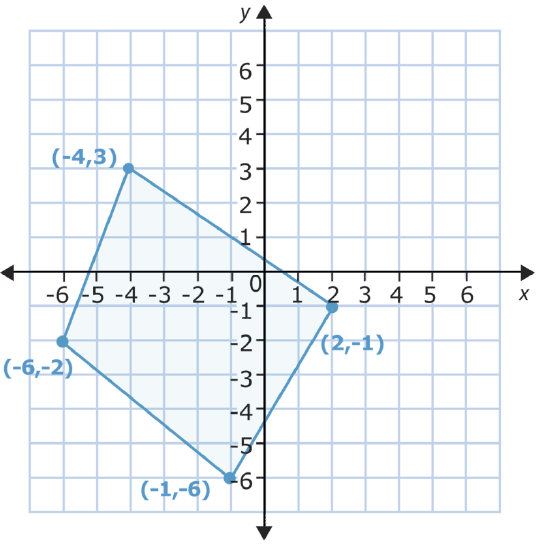
In this translation, you will move the figure to the right. That means the \(x\)-coordinates for each point will change but the \(y\)-coordinates will not. You simply count 5 places to the right from each point and make a new point.
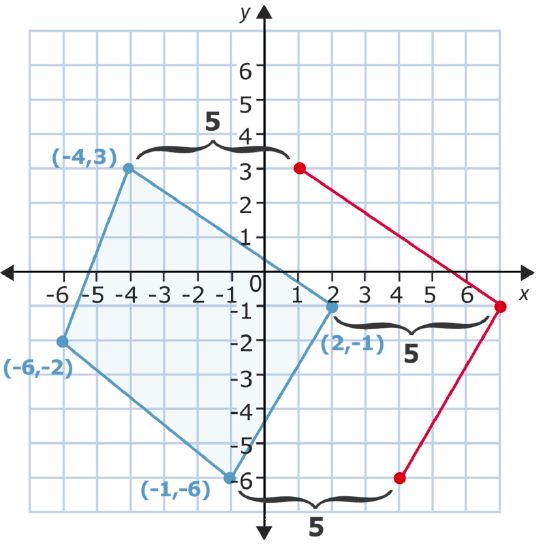
Once you relocate each point 5 places to the right, you can connect them to make the new figure that shows the translation.
You can check to see if you performed the translation correctly by adding 5 to each \(x\)-coordinate (because you moved to the right) and then checking these against the ordered pairs of the figure you drew. This is called coordinate notation. Notice that each point is represented by coordinates.
\(\begin{array}{lccc}
(-4,3) & (-6,-2) & (-1,-6) & (2,-1) \\
+5 & +5 & +5 & +5 \\
(1,3) & (-1,-2) & (4,-6) & (7,-1)
\end{array}\)
These are the points you graphed, so you have performed the translation correctly.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Mrs. Gilcrest and her special version of the game Battleship.
She translated the ships the same distance up or down, right or left. If the first ship is at (3, 6), (3, 7), (3, 8) and the second ship is translated 4 units to the right and 4 units up, what are the coordinates of the second ship?
Solution
First, remember the signs associated with a move to the right and a move up.
Right is a move in the positive direction on the \(x\)-axis and up is a move in the positive direction on the \(y\)-axis.
Next, add the moves to the coordinates.
(3+4, 6+4), (3+4, 7+4), (3+4, 8+4)
Then write the new vertices
(7, 10), (7, 11), (7, 12)
The coordinates of the second ship are (7, 10), (7, 11), (7, 12).
Example \(\PageIndex{2}\)
Solve this problem.
Slide the following figure 4 places to the left and 2 places up.
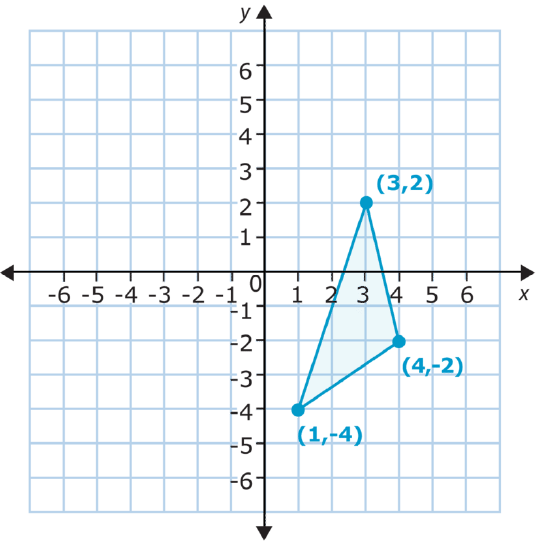
Solution
First, graph the new points.
Graph each point by counting 4 places to the left, and from there 2 places up.
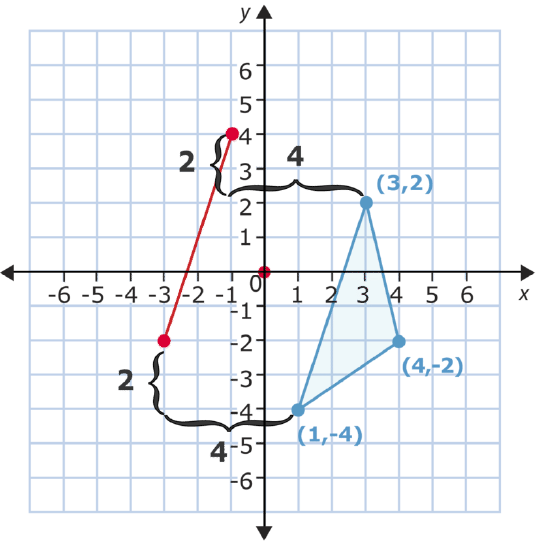
Then, form the new triangle.
Connect the new points.
You can check the translation by changing the \(x\)- and \(y\)-coordinates in the ordered pairs and then comparing these to the points you graphed. This time subtract 4 from each \(x\)-coordinate and add 2 to each \(y\)-coordinate. Let’s see what happens.
\(\begin{array}{ccc}
(3,2) & (4,-2) & (1,-4) \\
-4+2 & -4+2 & -4+2 \\
(-1,4) & (0,0) & (-3,-2)
\end{array}\)
Example \(\PageIndex{3}\)
Translate triangle \(\(ABC\)\) (0, 1), (1, 3), (4, 0) up 4.
Solution
First, remember whether up is a move on the \(x\)-axis or the \(y\)-axis.
Up is a move on the \(y\)-axis.
Next, add 4 to each of the \(y\)-values.
(0, 1+4), (1, 3+4), (4, 0+4)
Then, write the new vertices.
(0, 5), (1, 7), (4, 4)
The new triangle has coordinates (0, 5), (1, 7), (4, 4).
Example \(\PageIndex{4}\)
Translate Triangle \(DEF\) (-3, 2),(1, 6),(2, 1) down 2.
Solution
First, remember whether down is a move on the \(x\)-axis or the \(y\)-axis.
Down is a move on the \(y\)-axis.
Next, subtract 2 from each of the \(y\)-values.
(-3, 2-2), (1, 6-2), (2, 1-2)
Then, write the new vertices.
(-3, 0), (1, 4), (2, -1)
The new triangle has coordinates (-3, 0), (1, 4), (2, -1)
Example \(\PageIndex{5}\)
Translate triangle \(XYZ\) (-5, 4), (1, 8), (3, 5) to the right 3.
Solution
First, remember whether right is a move on the \(x\)-axis or the \(y\)-axis.
Right is a move on the \(x\)-axis.
Next, add 3 to each \(x\)-value.
(-5+3, 4), (1+3, 8), (3+3, 5)
Then write the new vertices
(-2, 4), (4, 8), (6, 5)
The new triangle has coordinates (-2, 4), (4, 8), (6, 5).
Review
Identify the transformations shown below as a translation, reflection, or rotation.

- True or false. This figure has been translated 5 places to the right.
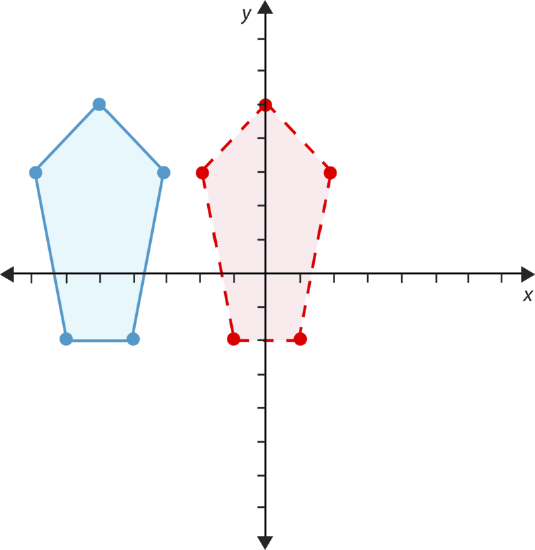
Translate each figure to the right 6 places and up 1. Then write the new coordinates for the figure.
- Triangle \(DEF\) (-1, 2)(1, 6)(2, 1)
- Triangle \(DEF\) (-3, 2)(1, 6)(2, 1)
- Triangle \(DEF\) (0, 2)(1, 6)(2, 1)
- Triangle \(DEF\) (4, -2)(1, 6)(2, 1)
- Triangle \(DEF\) (5, 3)(1, 6)(2, 1)
- Triangle \(DEF\) (4, 4)(1, 6)(2, 1)
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.18.
Resources
Vocabulary
| Term | Definition |
|---|---|
| \(x\)-axis | The \(x\)-axis is the horizontal axis in the coordinate plane, commonly representing the value of the input or independent variable. |
| \(y\)-axis | The \(y\)-axis is the vertical number line of the Cartesian plane. |
| Coordinate Plane | The coordinate plane is a grid formed by a horizontal number line and a vertical number line that cross at the (0, 0) point, called the origin. The coordinate plane is also called a Cartesian Plane. |
| Transformation | A transformation moves a figure in some way on the coordinate plane. |
Additional Resources
Video: Identify the Quadrant of a Point of the Coordinate System
Practice: Sliding Figures

