8.3: Reflection Symmetry
- Page ID
- 2164
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Property of a shape with one or more lines of symmetry.
A line of symmetry is a line that passes through a figure such that it splits the figure into two congruent halves such that if one half were folded across the line of symmetry it would land directly on top of the other half.

Reflection symmetry is present when a figure has one or more lines of symmetry. These figures have reflection symmetry:
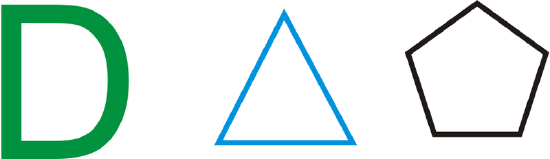
These figures do not have reflection symmetry:

What if you had a six-pointed star, you drew a line down it, and then you folded it along that line? If the two sides of the star lined up, what would that mean about the line?
Example \(\PageIndex{1}\)
Find all lines of symmetry for the shape below.
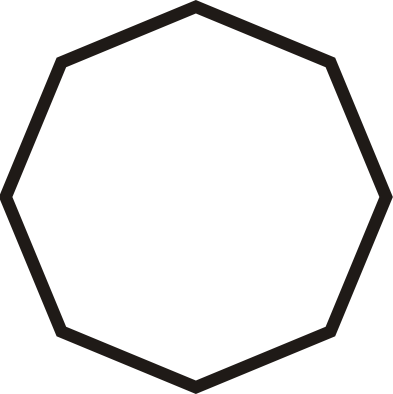
Solution
Draw lines through the figure so that the lines perfectly cut the figure in half. This figure has eight lines of symmetry.
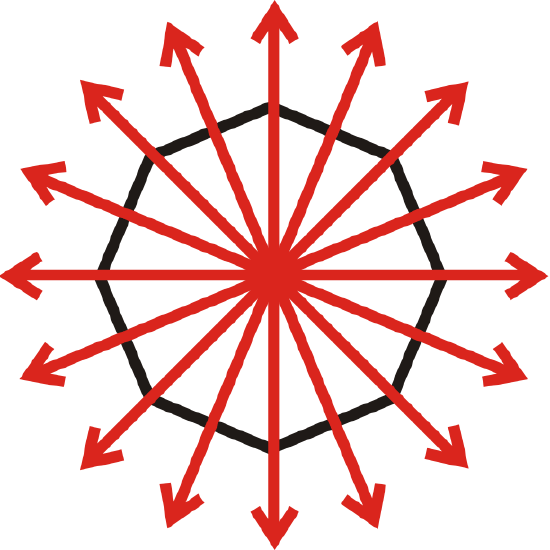
Example \(\PageIndex{2}\)
Find all lines of symmetry for the shape below.

Solution
You cannot draw lines through the figure so that the lines perfectly cut the figure in half, so this figure has no lines of symmetry.
Example \(\PageIndex{3}\)
Find all lines of symmetry for the shape below.

Solution
This figure has two lines of symmetry.
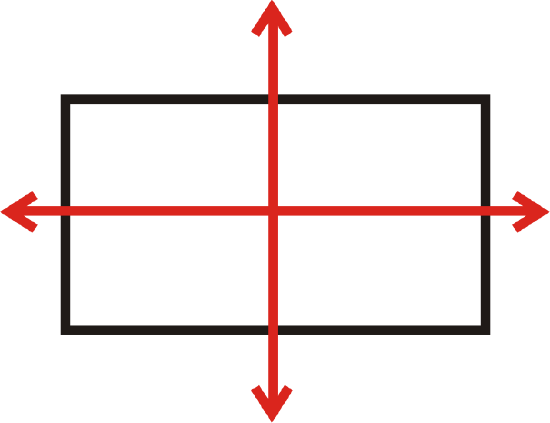
Example \(\PageIndex{4}\)
Does the figure below have reflection symmetry?

Solution
Yes, this figure has reflection symmetry.

Example \(\PageIndex{5}\)
Does the figure below have reflection symmetry?

Solution
Yes, this figure has reflection symmetry.

Review
Determine whether each statement is true or false.
- All right triangles have line symmetry.
- All isosceles triangles have line symmetry.
- Every rectangle has line symmetry.
- Every rectangle has exactly two lines of symmetry.
- Every parallelogram has line symmetry.
- Every square has exactly two lines of symmetry.
- Every regular polygon has three lines of symmetry.
- Every sector of a circle has a line of symmetry.
Draw the following figures.
- A quadrilateral that has two pairs of congruent sides and exactly one line of symmetry.
- A figure with infinitely many lines of symmetry.
Find all lines of symmetry for the letters below.
-

Figure \(\PageIndex{13}\) -

Figure \(\PageIndex{14}\) -

Figure \(\PageIndex{15}\) -

Figure \(\PageIndex{16}\) -

Figure \(\PageIndex{17}\)
Determine if the words below have reflection symmetry.
- OHIO
- MOW
- WOW
- KICK
- pod
Trace each figure and then draw in all lines of symmetry.
-
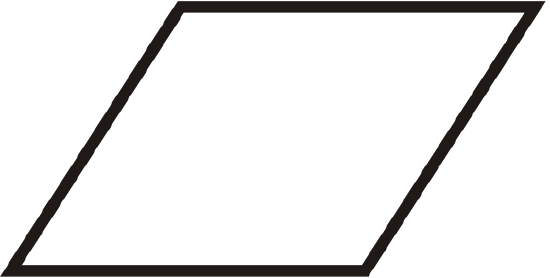
Figure \(\PageIndex{18}\) -
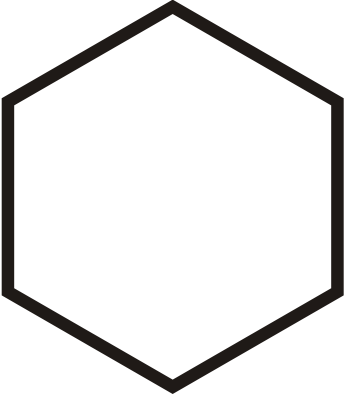
Figure \(\PageIndex{19}\) -

Figure \(\PageIndex{20}\)
Determine if the figures below have reflection symmetry. Identify all lines of symmetry.
-

Figure \(\PageIndex{13}\) -

Figure \(\PageIndex{13}\) -

Figure \(\PageIndex{13}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 12.1.
Vocabulary
| Term | Definition |
|---|---|
| Line of Symmetry | A line of symmetry is a line that can be drawn to divide a figure into equal halves. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Isosceles Triangle | An isosceles triangle is a triangle in which exactly two sides are the same length. |
| Line Symmetry | A figure has line symmetry or reflection symmetry when it can be divided into equal halves that match. |
| reflection symmetry | A figure has reflection symmetry if it can be reflected across a line and look exactly the same as it did before the reflection. |
| Symmetry | A figure has symmetry if it can be transformed and still look the same. |
Additional Resources
Interactive Element
Video: Reflection Symmetry Principles - Basic
Activities: Reflection Symmetry Discussion Questions
Study Aids: Symmetry and Tessellations Study Guide
Practice: Reflection Symmetry

