9.1: Polyhedrons
- Page ID
- 2166
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)3-D figures formed by polygons enclosing regions in space.
A polyhedron is a 3-dimensional figure that is formed by polygons that enclose a region in space. Each polygon in a polyhedron is a face. The line segment where two faces intersect is an edge. The point of intersection of two edges is a vertex.
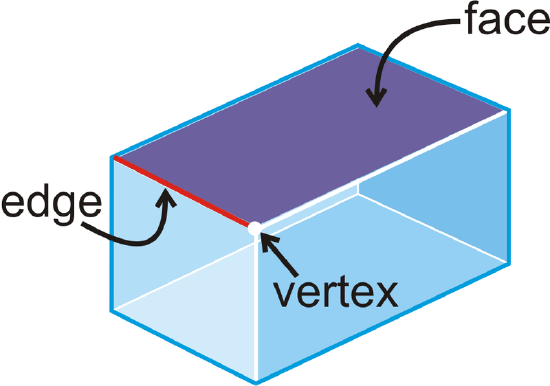
Examples of polyhedrons include a cube, prism, or pyramid. Cones, spheres, and cylinders are not polyhedrons because they have surfaces that are not polygons. The following are more examples of polyhedrons:
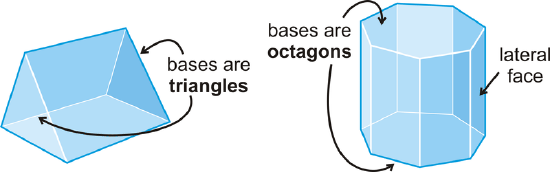
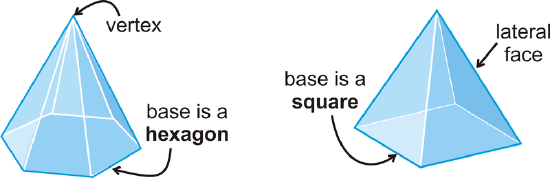
The number of faces (\(F\)), vertices (\(V\)) and edges (\(E\)) are related in the same way for any polyhedron. Their relationship was discovered by the Swiss mathematician Leonhard Euler, and is called Euler’s Theorem.
Euler’s Theorem: \(F+V=E+2\).
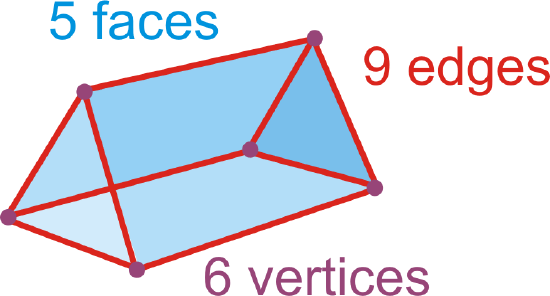
\(Faces+Vertices=Edges+2\)
\(5+6=9+2\)
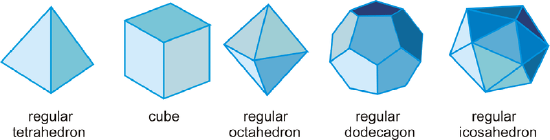
A regular polyhedron is a polyhedron where all the faces are congruent regular polygons. There are only five regular polyhedra, called the Platonic solids.
- Regular Tetrahedron: A 4-faced polyhedron and all the faces are equilateral triangles.
- Cube: A 6-faced polyhedron and all the faces are squares.
- Regular Octahedron: An 8-faced polyhedron and all the faces are equilateral triangles.
- Regular Dodecahedron: A 12-faced polyhedron and all the faces are regular pentagons.
- Regular Icosahedron: A 20-faced polyhedron and all the faces are equilateral triangles.
What if you were given a solid three-dimensional figure, like a carton of ice cream? How could you determine how the faces, vertices, and edges of that figure are related?
Example \(\PageIndex{1}\)
-
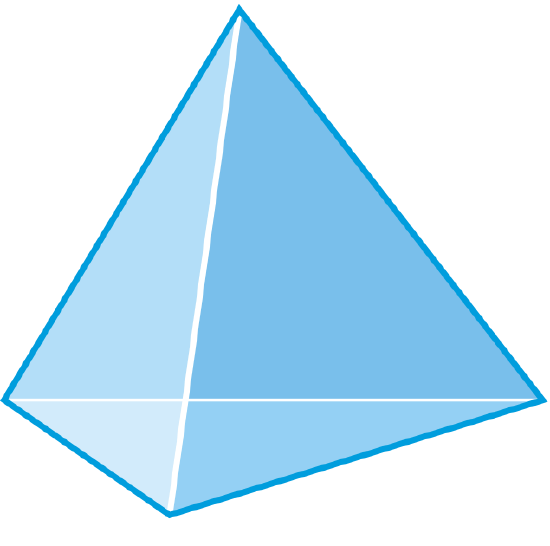
Figure \(\PageIndex{6}\) -
Figure \(\PageIndex{7}\) -

Figure \(\PageIndex{8}\)
Solution
The base is a triangle and all the sides are triangles, so this is a triangular pyramid, which is also known as a tetrahedron. There are 4 faces, 6 edges and 4 vertices.
Example \(\PageIndex{2}\)
In a six-faced polyhedron, there are 10 edges. How many vertices does the polyhedron have?
Solution
Solve for \(V\) in Euler’s Theorem.
\(\begin{aligned} F+V&=E+2 \\ 6+V&=10+2 \\ V&=6\end{aligned} \)
Therefore, there are 6 vertices.
Example \(\PageIndex{3}\)
Markus counts the edges, faces, and vertices of a polyhedron. He comes up with 10 vertices, 5 faces, and 12 edges. Did he make a mistake?
Solution
Plug all three numbers into Euler’s Theorem.
\(\begin{aligned} F+V&=E+2 \\ 5+10&=12+2 \\ 15 &\neq 14 \end{aligned}\)
Because the two sides are not equal, Markus made a mistake.
Example \(\PageIndex{4}\)
Find the number of faces, vertices, and edges in an octagonal prism.
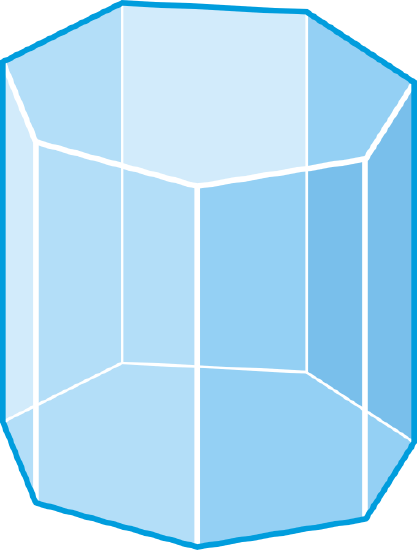
Solution
There are 10 faces and 16 vertices. Use Euler’s Theorem, to solve for \(E\).
\(\begin{aligned} F+V&=E+2 \\ 10+16&=E+2 \\ 24&=E \end{aligned}\)
Therefore, there are 24 edges.
Example \(\PageIndex{5}\)
A truncated icosahedron is a polyhedron with 12 regular pentagonal faces, 20 regular hexagonal faces, and 90 edges. This icosahedron closely resembles a soccer ball. How many vertices does it have? Explain your reasoning.

Solution
We can use Euler's Theorem to solve for the number of vertices.
\(\begin{aligned} F+V&=E+2 \\ 32+V&=90+2 \\ V&=60\end{aligned}\)
Therefore, it has 60 vertices.
Review
Complete the table using Euler’s Theorem.
| Name | Faces | Edges | Vertices | |
|---|---|---|---|---|
| 1. | Rectangular Prism | 6 | 12 | |
| 2. | Octagonal Pyramid | 16 | 9 | |
| 3. | Regular Icosahedron | 20 | 12 | |
| 4. | Cube | 12 | 8 | |
| 5. | Triangular Pyramid | 4 | 4 | |
| 6. | Octahedron | 8 | 12 | |
| 7. | Heptagonal Prism | 21 | 14 | |
| 8. | Triangular Prism | 5 | 9 |
Determine if the following figures are polyhedra. If so, name the figure and find the number of faces, edges, and vertices.
-
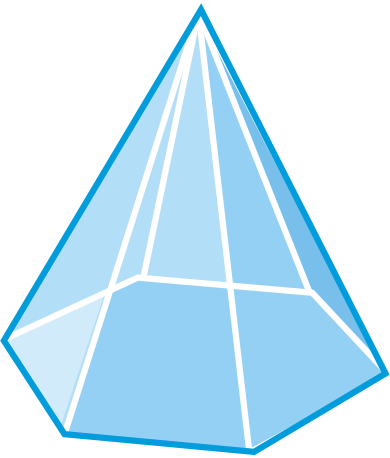
Figure \(\PageIndex{11}\) -

Figure \(\PageIndex{12}\) -
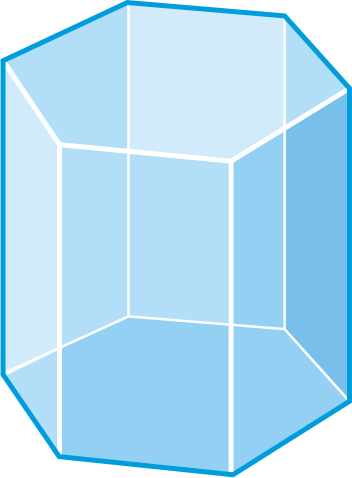
Figure \(\PageIndex{13}\) -

Figure \(\PageIndex{14}\) -
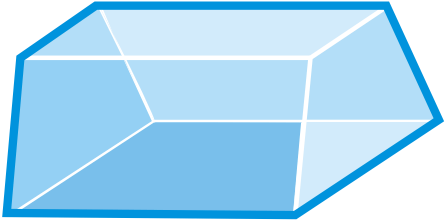
Figure \(\PageIndex{15}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 11.1.
Additional Resources
Video: Polyhedrons Principles - Basic
Activities: Polyhedrons Discussion Questions
Study Aids: Polyhedra Study Guide
Practice: Polyhedrons
Real World: Roly Poly Polyhedron!

