9.23: Surface Area of Cones
- Page ID
- 6735
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)NEEDS CONTENT FROM GEO.858
Robbie is building a base for a cylindrical fan to put in his room. The truncated cone has a larger radius of 3 feet, a smaller radius of 2 feet, and a slant height of 3 ft. He is going to paint the stand and needs to find the surface area of the base to figure out how much paint to buy. How can Robbie figure out the surface area?
In this concept, you will learn to find the surface area cones and truncated cones.
Surface Area
Cones are three-dimensional figures that have a circular base and a point at the top. You can calculate the surface area of a cone using a net or a formula. Surface area is the total of the areas of each face in a solid figure.
Here is what the net of a cone would look like.
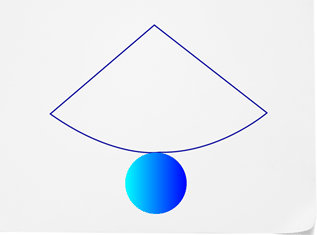
The shaded circle is the base. Remember, cones always have circular bases. The un-shaded portion of the cone represents its side. Technically you don’t call this a face because it has a round edge.
To find the surface area of a cone, you need to calculate the area of the circular base and the side and add them together. The formula for finding the area of a circle is \(A&=\pi r^{2}\), where r is the radius of the circle. You use this formula to find the area of the circular base.
To find the area of the cone’s side, you multiply the radius (\(r\)), the slant height (\(s\)), and \(\pi\).
\(A=\pi rs\)
Let’s look at an example.
Find the surface area of the following cone.
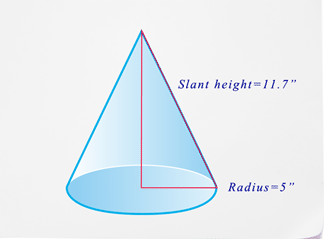Figure \(\PageIndex{4}\)First, calculate the area of the base.
\(\begin{aligned}A&=\pi r^{2} \\ A&=\pi (5)^{2}\\ A&=78.5\end{aligned}\)
Next, calculate the area of the sector, also known as the lateral surface area.
\(\begin{aligned}A&=\pi (5)(11.7) \\ A&=183.8\end{aligned}\)
Then, add the area of the base to the lateral surface area.
\(\begin{aligned} A&=\text{base} +\text{lateral Surface} \\ A&=78.5+183.8 \\ A&=262.3\end{aligned}\)
The answer is 262.3.
The surface area of the cone is \(262.3 \text{ in}^{2}\).
A short cut would be to simply use the formula to find the surface area of a cone. Here is the formula for finding the surface area of a cone: \(SA&=\pi r^{2}+\pi rs\).
The first part of the formula, \(\pi r^{2}\), is simply the area formula for circles. This represents the base area. The second part, \pi rs, represents the lateral surface area of the cone’s side. You can simply put the pieces together and solve for the area of both parts at once.
A truncated cone is one where the point of the cone is cut off leaving two circular bases and a side face.
Below is an image of what a truncated cone looks like.
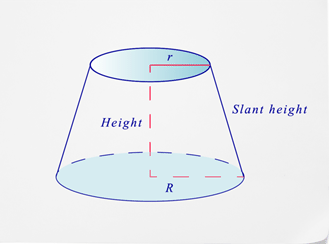
Notice that with a truncated cone you will have two different circular bases - a top radius and a bottom one. You will have to find the area of both bases plus the area of the sector to find the surface area.
The formula for finding the surface area of a truncated cone is:
\(SA=\pi [s(R+r)+r^{2}+r^{2}]\)
Notice that s stands for slant height, the capital R stands for the larger radius and the lowercase r stands for the smaller radius.
Let’s look at an example.
What is the surface area of a truncated cone with a slant height of 6 cm, a radius of 8 cm and a radius of 6 cm?
First, fill in all you know into the surface area formula.
\(\begin{aligned}SA&=\pi [s(R+r)+r^{2}+r^{2}] \\ SA&=\pi [6(8+6)+8^{2}+6^{2}]\end{aligned}\)
Next, use algebra to solve for the surface area.
\(\begin{aligned}SA&=\pi [6(8+6)+8^{2}+6^{2}] \\ SA&=\pi [6(14)+64+36] \\ SA&=\pi [84+64+36] \\ SA&=\pi [184] \\ SA&=578.1\end{aligned}\)
The answer is 578.1.
The surface area of the cone is \(578.1\text{ cm}^2\).
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Robbie’s fan stand.
Robbie is building a stand in the shape of a truncated cone. The bottom circular base has a radius of 3 ft. The circular top has a radius of 2 ft. The slant height for the stand is 3 ft. Robbie has to find the surface area so that he knows how much paint he needs.
Solution
First, substitute what you know into the surface area formula.
\(\begin{aligned}SA&=\pi [s(R+r)+r^{2}+r^{2}] \\ SA&=\pi [3(3+2)+3^{2}+2^{2}]\end{aligned}\)
Next, use algebra to solve for the surface area.
\(\begin{aligned}SA&=\pi [3(3+2)+3^{2}+2^{2}] \\ SA&=\pi [3(5)+9+4] \\ SA&=\pi [15+9+4] \\ SA&=\pi [28] \\ SA&=87.96\end{aligned}\)
The answer is 87.96.
Robbie needs enough paint to cover \(88\text{ ft}^2\).
Example \(\PageIndex{2}\)
Trey is decorating conical party hats for his party by wrapping them in colored tissue paper. Each hat has a radius of 4.2 centimeters and a slant height of 8.6 centimeters. If he wants to wrap six party hats, how much paper will he need?
Solution
First, substitute what you know into the surface area formula.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (4.2)2+\pi (4.2)(8.6)\end{aligned}\)
Next, use algebra to solve for the surface area.
\(\begin{aligned}SA&=\pi (4.2)^{2}+\pi (4.2)(8.6) \\ SA&=\pi (17.64)+\pi (36.12) \\ SA&=55.4+113.5 \\ SA&=168.9\end{aligned}\)
Then, find the total area of the 6 hats.
\(SA_{total}&=6×SA^{one\: hat} 89 \\ SA_{total}&=6×168.9 \\SA_{total}&=1013.4\end{aligned}\)
The answer is 1013.4.
Trey would need 1013.4 cm2 of paper to make the six hats.
Example \(\PageIndex{3}\)
Find the surface area of a cone with a radius of 4 inches and a slant height of 6 inches.
Solution
First, substitute what you know into the surface area formula.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (4)2+\pi (4)(6)\end{aligned}\)
Next, use algebra to solve for the surface area.
\(\begin{aligned}SA&=\pi (4)^{2}+\pi (4)(6) \\ SA&=\pi (16)+\pi (24) \\ SA&=50.3+75.4\\ SA&=125.7\end{aligned}\)
The answer is 125.7.
The surface area of the cone is \(125.7 \text{ in}^{2}\).
Example \(\PageIndex{4}\)
Find the surface area of a cone with a radius of 5 feet and a slant height of 8 feet.
Solution
First, substitute what you know into the surface area formula.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (5)2+\pi (5)(8)\end{aligned}\)
Next, use algebra to solve for the surface area.
\(\begin{aligned}SA&=\pi (5)^{2}+\pi (5)(8) \\ SA&=\pi (25)+\pi (40) \\ SA&=78.5+125.7 \\ SA&=204.2\end{aligned}\)
The answer is 204.2.
The surface area of the cone is \(204.2\text{ ft}^2\).
Example \(\PageIndex{5}\)
Find the surface area of a cone with a radius of 3 inches and a slant height of 4.5 inches.
Solution
First, substitute what you know into the surface area formula.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (3)^{2}+\pi (3)(4.5)\end{aligned}\)
Next, use algebra to solve for the surface area.
\(\begin{aligned} SA&=\pi (3)^{2}+\pi (3)(4.5) \\ SA&=\pi (9)+\pi (13.5) \\ SA&=28.3+42.4 \\ SA&=70.7\end{aligned}\)
The answer is 70.7.
The surface area of the cone is \(70.7 \text{ in}^{2}\).
Review
Answer the questions below each of the following diagrams
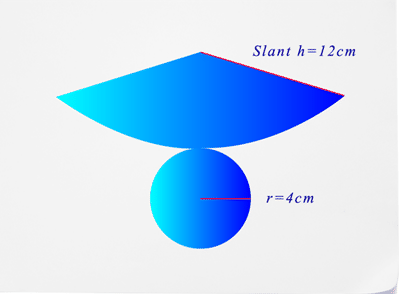
- What is the name of the figure represented in this net?
- What is the diameter of this figure?
- What is the slant height of the figure?
- What is the surface area of the figure?
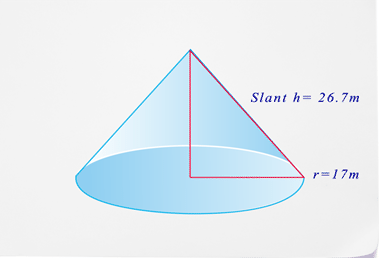
- What is the name of this figure?
- What is the shape of the base?
- What is the diameter of the base?
- What is the surface area of this figure?
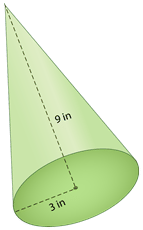
- What is the name of this figure?
- What is the shape of the base?
- What is the diameter of the base?
- What is the surface area of this figure?
Find the surface area of each cone.
- \(r=4\text{ in}\), \(sh=5\text{ in}\)
- \(r=5 \text{ m}\), \(sh=7 \text{ m}\)
- \(r=3 \text{ cm}\), \(sh=6\text{ cm}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.9.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Cone | A cone is a solid three-dimensional figure with a circular base and one vertex. |
| Net | A net is a diagram that shows a “flattened” view of a solid. In a net, each face and base is shown with all of its dimensions. A net can also serve as a pattern to build a three-dimensional solid. |
| Sector | A sector of a circle is a portion of a circle contained between two radii of the circle. Sectors can be measured in degrees. |
| Surface Area | Surface area is the total area of all of the surfaces of a three-dimensional object. |
| Slant Height | The slant height is the height of a lateral face of a pyramid. |
Additional Resources
Video: Surface Area of Cone - Overview
Practice: Surface Area of Cones