9.24: Volume of Cones
- Page ID
- 6736
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Volume equals the area of the base times \(\dfrac{1}{3}\) of the height.

Finding the Volume of a Cone
To figure out the volume of a cone, let’s first look at how you can compare it with another solid figure. The closest solid figure to a cone is a cylinder. Both cones and cylinders have circular bases. The difference between the two is while a cylinder has two circular bases, a cone only has one.
Here is a cylinder and the formula for finding the volume of a cylinder.

\(V&=\pi r^{2} h\)
In the picture below, you can see how a cylinder and a cone are related:
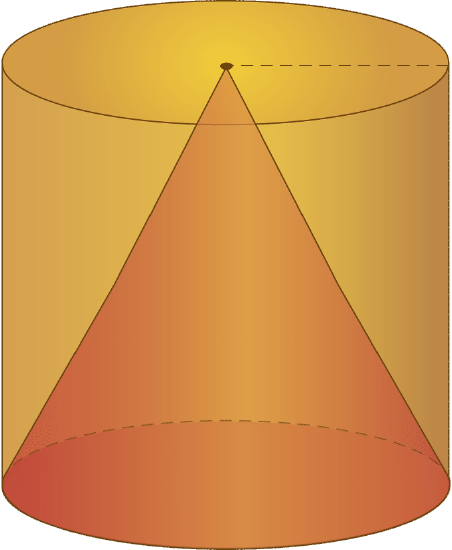
To find the volume of the cone, you use a formula similar to that of a pyramid, except that you are going to take into consideration that the base of a cone is a circle. Therefore, you will need to find the area of the circle to find the volume of the cone. The formula for the area of a circle is \(\pi r^{2}\). Take that measurement and multiply it by the height of the cone. Next, because the cone fills a portion of the cylinder, multiply the product by one-third.
\(V&=\dfrac{1}{3} \pi r^{2} h\)
Let's look at an example. What is the volume of the cone below?
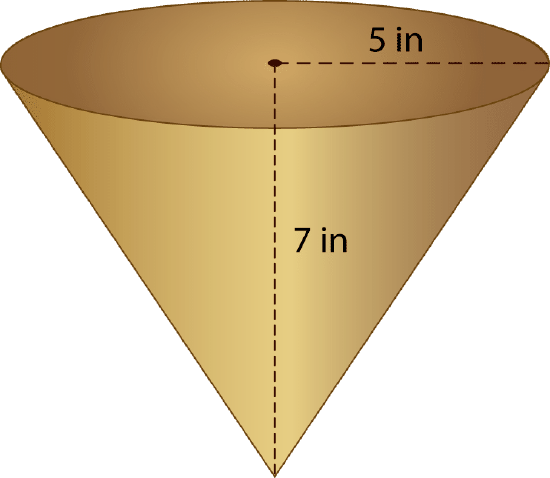
First, substitute the given values into the formula.
\(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(52)(7) \\ V&=\dfrac{1}{3} (3.14)(25)(7) \\ V&=\dfrac{1}{3} (3.14)(175)\\ V&=\dfrac{549.5}{3} \\ V&=183.16 \text{ in}^{3}\end{aligned}\)
The answer is the volume of the cone is 183.16 cubic inches.
Let's look at another example. Find the volume of the following cone.
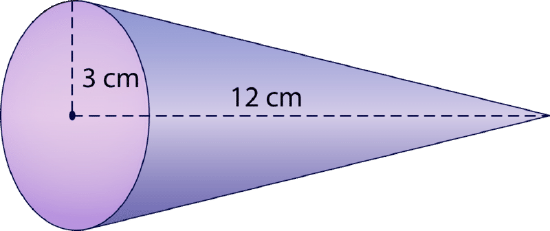
First, substitute the given values into the formula.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(3^{2})(12) \\ V&=\dfrac{1}{3} (3.14)(9)(12) \\ V&=\dfrac{1}{3} (3.14)(108) \\ V&=\dfrac{339.12}{3} \\ V&=113.04 cm^{3}\end{aligned}\)
The volume of the cone is \(113.04\text{ cm}^3\).
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Francine's new dessert cups.
She needs to figure out the volume of ice cream that will fit into one dessert cup. The diameter of the cup is 3 inches and the height is 6 inches.
Solution
First, find the value of the radius by dividing the diameter by 2, and substitute the values for pi, the radius, and the height of the cone into the formula for volume of a cone.
\(\begin{aligned}r&=1.5 \\ r&=3\divide 2 \\ V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(1.52)(6)\end{aligned}\)
Next, square the radius and multiply the values together.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(1.52)(6) \\ V&=\dfrac{1}{3} (3.14)(2.25)(6) \\ V&=\dfrac{1}{3} (3.14)(13.5) \\ V&=42.393\end{aligned}\)
Then, divide by 3 and record the answer, remembering to include the appropriate unit of measurement.
\(\begin{aligned}V&=42.393 \\ V&=14.13 \text{ in}^{3}\end{aligned}\)
The answer is the volume of ice cream that will fill Francine's cone-shaped desert cup is 16.75 cubic inches.
Example \(\PageIndex{2}\)
Find the volume of a cone with a radius of 2 inches and a height of 4 inches.
Solution
First, substitute the values for pi, the radius, and the height of the cone into the formula for volume of a cone.
\(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(2^{2})(4)\end{aligned}\)
Next, square the radius and multiply the values together.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(2^{2})(4) \\ V&=\dfrac{1}{3} (3.14)(4)(4) \\ V&=\dfrac{1}{3} (3.14)(16) \\ V&=50.243\end{aligned}\)
Then, divide by 3 and record the answer, remembering to include the appropriate unit of measurement.
\(\begin{aligned}V&=\dfrac{50.24}{3} \\ V&=16.75 \text{ in}^{3}\end{aligned}\)
The answer is the volume of the cone is 16.75 cubic inches.
Example \(\PageIndex{3}\)
Find the volume of a cone with a radius of 5 ft and a height of 8 ft.
Solution
First, substitute the values for pi, the radius, and the height of the cone into the formula for volume of a cone.
\(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(52)(8)\end{aligned}\)
Next, square the radius and multiply the values together.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(52)(8) \\ V&=\dfrac{1}{3} (3.14)(25)(8) \\ V&=\dfrac{1}{3} (3.14)(200) \\ V&=\dfrac{628}{3}\end{aligned}\)
Then, divide by 3 and record the answer, remembering to include the appropriate unit of measurement.
\(\begin{aligned}V&=\dfrac{628}{3} \\ V&=209.33 \text{ in}^{3}\end{aligned}\)
The answer is the volume of the cone is 209.33 cubic inches.
Example \(\PageIndex{4}\)
A cone with a radius of 4 m and a height of 9 m.
Solution
First, substitute the values for pi, the radius, and the height of the cone into the formula for volume of a cone.
\(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(4^{2})(9)\end{aligned}\)
Next, square the radius and multiply the values together.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(4^{2})(9) \\ V&=\dfrac{1}{3} (3.14)(16)(9) \\ V&=\dfrac{1}{3} (3.14)(144) \\ V&=\dfrac{452.16}{3}\end{aligned}\)
Then, divide by 3 and record the answer, remembering to include the appropriate unit of measurement.
\(\begin{aligned} V&=\dfrac{452.16}{3} \\ V&=150.72 \text{ m}^{3}\end{aligned}\)
The answer is the volume of the cone is 150.72 cubic meters.
Review
Find the volume of each cone.
- A cone with a radius of 3 inches and a height of 7 inches.
- A cone with a radius of 5 ft and a height of 9 ft.
- A cone with a radius of 6 meters and a height of 10 meters.
- A cone with a radius of 10 inches and a height of 12 inches.
- A cone with a radius of 12 mm and a height of 14 mm.
- A cone with a radius of 5 ft and a height of 12 feet.
- A cone with a radius of 4.5 inches and a height of 7 inches.
- A cone with a radius of 3.5 inches and a height of 5.5 inches.
- A cone with a radius of 7 cm and a height of 13 cm.
- A cone with a radius of 8 cm and a height of 11 cm.
- A cone with a radius of 7.5 inches and a height of 11 inches.
- A cone with a radius of 11.5 inches and a height of 15 inches.
- A cone with a radius of 12.5 feet and a height of 15 feet.
Solve each word problem.
- A cone has a radius of 6 meters and a height of 14 meters. What is its volume?
- The containers of icing for Tina’s cake decorator are cones. Each container has a radius of 2.4 inches and a height of 7 inches. If Tina buys containers of red, yellow, and blue icing, how much icing will she buy?
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.15.
Vocabulary
| Term | Definition |
|---|---|
| Cone | A cone is a solid three-dimensional figure with a circular base and one vertex. |
| Pyramid | A pyramid is a three-dimensional object with a base that is a polygon and triangular faces that meet at one vertex. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
Additional Resources
Interactive Element
Video: Determine the Volume of a Cone
Practice: Volume of Cones

