9.25: Surface Area and Volume of Spheres
- Page ID
- 6748
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Derive and use the formula: volume equals \(\dfrac{4}{3}\) times pi times the radius cubed.
Spheres
Consider a solid figure consisting of the set of all points in three-dimensional space that are equidistant from a single point. How could you determine how much two-dimensional and three-dimensional space that figure occupies?
A sphere is the set of all points in three-dimensional space that are equidistant from a single point. The radius of a sphere has one endpoint on the sphere surface and the other endpoint at the center of that sphere. The diameter of a sphere must contain the center.
A great circle is the largest circular cross-section in a sphere. The circumference of a sphere is the circumference of a great circle. Every great circle divides a sphere into two congruent hemispheres.
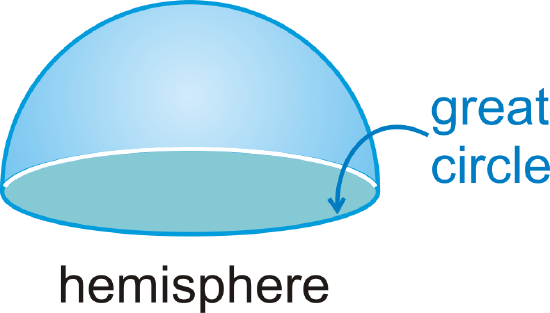
Surface Area
Surface area is a two-dimensional measurement that is the total area of all surfaces that bound a solid. The basic unit of area is the square unit.
Surface Area of a Sphere: \(SA=4\pi r^{2}\)
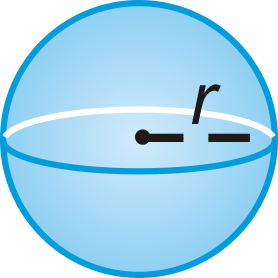
Volume
To find the volume of any solid you must figure out how much space it occupies. The basic unit of volume is the cubic unit.
Volume of a Sphere: \(V=\dfrac{4}{3}\pi r^{3}\)
Example \(\PageIndex{1}\)
Find the surface area of the figure below, a hemisphere with a circular base.
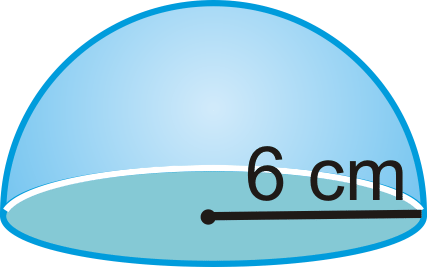
Solution
Use the formula for surface area:
\(\begin{aligned} SA&=\pi r^{2} +124\pi r^{2} \\ &=\pi (6^{2})+2\pi (6^{2}) \\&=36\pi +72\pi =108\pi \text{ cm}^{2}\end{aligned}\)
Example \(\PageIndex{2}\)
A sphere has a volume of 14,137.167 ft3. What is the radius?
Solution
Use the formula for volume, plug in the given volume and solve for the radius, r:
\(\begin{aligned} V&=\dfrac{4}{3}\pi r^{3} \\ 14,137.167&=\dfrac{4}{3}\pi r^{3} \\ \dfrac{3}{4\pi} \cdot 14,137.167&=r^{3} \\ 3375&\approx r^{3}\end{aligned}\)
At this point, you will need to take the cubed root of 3375. Your calculator might have a button that looks like \sqrt[3]{ }, or you can use \(3375^{\dfrac{1}{3}}\).
\(\sqrt[3]{3375}=15\approx r\)
Example \(\PageIndex{3}\)
The circumference of a sphere is 26\pi feet. What is the radius of the sphere?
Solution
The circumference is referring to the circumference of a great circle.
Use \(C=2\pi r\):
\(\begin{aligned} 2\pi r&=26\pi \\ r&=13\text{ ft}\end{aligned}\)
Example \(\PageIndex{4}\)
Find the surface area of a sphere with a radius of 14 feet.
Solution
Use the formula for surface area:
\(SA=4\pi (14)^{2}\)
\(=784\pi \text{ ft}^{2}\)\)
Example \(\PageIndex{5}\)
Find the volume of a sphere with a radius of 6 m.
Solution
Use the formula for volume:
\(\begin{aligned} V&=\dfrac{4}{3}\pi 63 \\ &=\dfrac{4}{3}\pi (216) \\ &=288\pi \text{ m}^{3}\end{aligned}\)
Review
- Are there any cross-sections of a sphere that are not a circle? Explain your answer.
- List all the parts of a sphere that are the same as a circle.
- List any parts of a sphere that a circle does not have.
For 4 - 11, find the surface area and volume of a sphere with the given dimension. Leave your answer in terms of \(\pi\).
- a radius of 8 in.
- a diameter of 18 cm.
- a radius of 20 ft.
- a diameter of 4 m.
- a radius of 15 ft.
- a diameter of 32 in.
- a circumference of \(26\pi \text{ cm}\).
- a circumference of \(50\pi\text{ yds}\).
- The surface area of a sphere is \(121\pi \text{ in}^{2}\). What is the radius?
- The volume of a sphere is \(47916\pi \text{ m}^{3}\). What is the radius?
- The surface area of a sphere is \(4\pi \text{ ft}^{2}\). What is the volume?
- The volume of a sphere is \(36\pi \text{ mi}^{3}\). What is the surface area?
- Find the radius of the sphere that has a volume of \(335 \text{ cm}^{3}\). Round your answer to the nearest hundredth.
- Find the radius of the sphere that has a surface area \(225\pi \text{ ft}^{2}\).
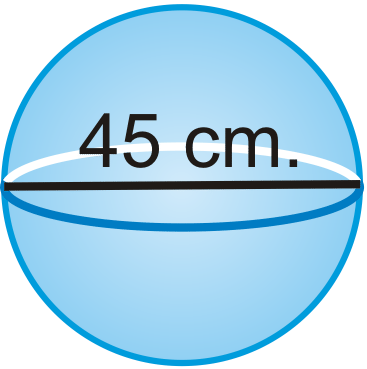
Find the surface area and volume of the following shape. Leave your answers in terms of \pi .
Review (Answers)
To see the Review answers, open this PDF file and look for section 11.7.
Vocabulary
| Term | Definition |
|---|---|
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| Sphere | A sphere is a round, three-dimensional solid. All points on the surface of a sphere are equidistant from the center of the sphere. |
| Radius | The radius of a circle is the distance from the center of the circle to the edge of the circle. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
| Cavalieri's Principle | States that if two solids have the same height and the same cross-sectional area at every level, then they will have the same volume. |
Additional Resources
Interactive Element
Video: Spheres Principles - Basic
Activities: Spheres Discussion Questions
Study Aids: Spheres Study Guide
Practice: Surface Area and Volume of Spheres
Real World: Where We Live!