9.27: Volume of Spheres
- Page ID
- 6750
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Maria has a paperweight that is a glass sphere. The sphere is full of liquid. If the diameter of the paperweight is 6 inches, how much liquid does it contain?
In this concept, you will learn to calculate the volume of spheres.
Volume
Volume is the measure of three-dimensional space a figure takes up. You can also think of it as how much space the figure “holds.”
To find the volume of spheres, you can use pyramids. Imagine a pyramid with its base on the surface of the sphere and its point as the center of the sphere. The radius of the sphere would be the height of the pyramid.
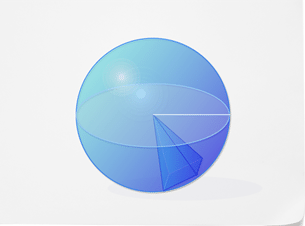
The pyramid makes up a portion of the sphere’s volume. If you can fill the whole sphere with pyramids like this, you would know the volume of the sphere. It would be equal to the volumes of all the pyramids put together. How many pyramids would it take to fill a sphere? That depends on the surface area of the sphere.
You can combine the surface area of a sphere with the volume formula for a pyramid to calculate the volume of all the pyramids contained within the sphere.
The formula for the volume of a pyramid is \(V=\dfrac{1}{3}Bh\).
You know that the height of the pyramid is the radius (r) of the sphere and the base of the pyramid is the surface area of the sphere (\(SA=4\pi r^2\)). If you substitute this information into the formula for the volume of a pyramid, you would get the following.
\(\begin{aligned}V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(4\pi r^{2})r \\ V&=\dfrac{4}{3} \pi r^{3}\end{aligned}\)
The volume of a sphere can be found using the formula
\(V=\dfrac{4}{3}\pi r^{3}\)
Again, all you need to know is the radius of the sphere. You put the value in for r in the formula and solve for \(V\), the volume.
Let’s look at an example.
Find the volume of the sphere below.
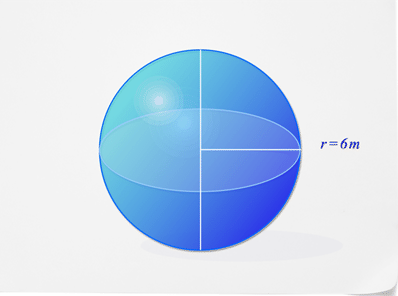
First, substitute what you know into the volume formula.
\(\begin{aligned} V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (6)^{3}\end{aligned}\)
Next, use algebra to calculate the volume.
\(\begin{aligned} V&=\dfrac{4}{3}\pi (6)^{3} \\ V&=\dfrac{4}{3}\pi (216) \\ V&=288\pi \\ V&=904.78\end{aligned}\)
The answer is 904.78.
The volume of the sphere is \(904.78 \text{ m}^{3}\).
If you wanted to make your measurement more accurate, you could say that the volume is \(288\pi m^{3}\).
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Maria’s liquid paperweight.
Maria has a paperweight with a diameter of 6 inches that is full of water, and she wants to find out how much liquid is inside.
Solution
First, find the radius of the sphere. Remember the radius is half the diameter.
\(\begin{aligned}r&=\dfrac{d}{2} \\ r&=\dfrac{6}{2} \\ r&=3 \end{aligned}\)
Next, substitute what you know into the volume formula.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (3)^{3}\end{aligned}\)
Then, use algebra to calculate the volume.
\(\begin{aligned} V&=\dfrac{4}{3}\pi (3)^{3} \\ V&=\dfrac{4}{3}\pi \\ V&=(27)^{3}6\pi \\ V&=113.10v\end{aligned}\)
The answer is 113.10.
The volume contained in Maria’s paperweight is \(113.10 \text{ in}^{3}\) or \(36\pi \text{ in}^{3}\).
Example \(\PageIndex{2}\)
Find the volume of the following sphere.

Solution
First, substitute what you know into the volume formula.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (8)^{3}\end{aligned}\)
Next, use algebra to calculate the volume.
\(\begin{aligned}V&=\dfrac{4}{3}\pi (8)^{3} \\ V&=\dfrac{4}{3}\pi (512) \\ V&=682.67\pi \\ V&=2144.66\end{aligned}\)
The answer is 2144.66. The volume of the sphere is \(2144.66 cm^{3}\).
If you wanted to make your measurement more accurate, you could say that the volume is \(682.67\pi cm^3\).
Example \(\PageIndex{3}\)
Find the volume of a sphere with a radius of 4 inches.
Solution
First, substitute what you know into the volume formula.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (4)^{3}\end{aligned}\)
Next, use algebra to calculate the volume.
\(\begin{aligned}V&=\dfrac{4}{3}\pi (4)^{3} \\ V&=\dfrac{4}{3}\pi (64) \\ V&=85.33\pi \\ V&=268.08\end{aligned}\)
The answer is 268.08.
The volume of the sphere is \(268.08 \text{ in}^{3}\).
Example \(\PageIndex{4}\)
Find the volume of a sphere with a radius of 5 ft.
Solution
First, substitute what you know into the volume formula.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (5)^{3}\end{aligned}\)
Next, use algebra to calculate the volume.
\(\begin{aligned}V&=\dfrac{4}{3}\pi (5)^{3} \\ V&=\dfrac{4}{3}\pi (125) \\ V&=166.67\pi \\ V&=523.60\end{aligned}\)
The answer is 523.60.
The volume of the sphere is \(523.60 \: ft^{3}\).
Example \(\PageIndex{5}\)
Find the volume of a sphere with a radius of 3.5 inches.
Solution
First, substitute what you know into the volume formula.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (3.5)^{3}\end{aligned}\)
Next, use algebra to calculate the volume.
\(\begin{aligned} V&=\dfrac{4}{3}\pi (3.5)^{3} \\ V&=\dfrac{4}{3}\pi (42.875) \\ V&=57.17\pi \\ V&=179.59\end{aligned}\)
The answer is 179.59.
The volume of the sphere is \(179.59 \text{ in}^{3}\).
Review
Find the volume of each sphere. You may round to the nearest hundredth when necessary.
1. A sphere with a radius of 3 m.
2. A sphere with a radius of 2.5 m.
3. A sphere with a radius of 5 in.
4. A sphere with a radius of 6 in.
5. A sphere with a radius of 7 ft.
6. A sphere with a radius of 4.5 cm.
7. A sphere with a radius of 5.5 m.
8. A sphere with a radius of 13 mm.
9. A sphere with a diameter of 8 in.
10. A sphere with a diameter of 10 ft.
11. A sphere with a diameter of 3 m.
12. A sphere with a diameter of 13 m.
13. A sphere with a diameter of 22 ft.
Use what you have learned to solve each problem.
14. A sphere has a diameter of 12 feet. What is its volume?
15. Kelly has a perfume bottle in the shape of a sphere. The diameter of the bottle is 6 inches. How much perfume does Kelly have left if the bottle is only half full?
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.15.
Vocabulary
| Term | Definition |
|---|---|
| Sphere | A sphere is a round, three-dimensional solid. All points on the surface of a sphere are equidistant from the center of the sphere. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
Additional Resources
Video: Volume of a Sphere
Practice: Volume of Spheres

