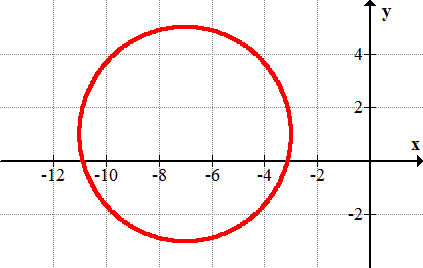9.3 Circles
- Page ID
- 1034
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A circle is the collection of points that are the same distance from a single point. What is the connection between the Pythagorean Theorem and a circle?
Graphing Circles
The single point that all the points on a circle are equidistant from is called the center of the circle. A circle does not have a focus or a directrix, instead it simply has a center. Circles can be recognized immediately from the general equation of a conic when the coefficients of \(x^{2}\) and \(y^{2}\) are the same sign and the same value. Circles are not functions because they do not pass the vertical line test. The distance from the center of a circle to the edge of the circle is called the radius of the circle. The distance from one end of the circle through the center to the other end of the circle is called the diameter. The diameter is equal to twice the radius.
The graphing form of a circle is:
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
The center of the circle is at \((h, k)\) and the radius of the circle is \(r\). Note that this looks remarkably like the Pythagorean Theorem.
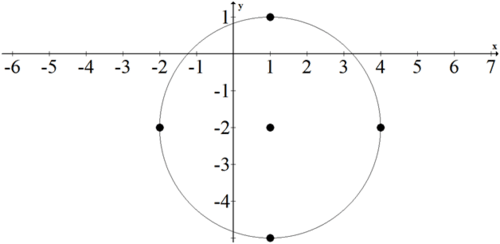
To graph a circle, first plot the center and then apply the radius. Take the following equation for a circle:
\((x-1)^{2}+(y+2)^{2}=9\)
The center is at (1,-2) . Plot that point and the four points that are exactly 3 units from the center.
Examples
Earlier, you were asked about the connection between circles and the Pythagorean Theorem. The reason why the graphing form of a circle looks like the Pythagorean Theorem is because each \(x\) and \(y\) coordinate along the outside of the circle forms a perfect right triangle with the radius as the hypotenuse.
Graph the following conic: \((x+2)^{2}+(y-1)^{2}=1\)
Turn the following equation into graphing form for a circle. Identify the center and the radius.
\(36 x^{2}+36 y^{2}-24 x+36 y-275=0\)
Complete the square and then divide by the coefficient of \(x^{2}\) and \(y^{2}\)
\(36 x^{2}-24 x+36 y^{2}+36 y=275\)
\(36\left(x^{2}-\frac{2}{3} x+\underline{-}\right)+36\left(y^{2}+y+\underline{x}\right)=275\)
\(36\left(x^{2}-\frac{2}{3} x+\frac{1}{9}\right)+36\left(y^{2}+y+\frac{1}{4}\right)=275+4+9\)
\(36\left(x-\frac{1}{3}\right)^{2}+36\left(y+\frac{1}{2}\right)^{2}=288\)
\(\left(x-\frac{1}{3}\right)^{2}+\left(y+\frac{1}{2}\right)^{2}=8\)
The center is \(\left(\frac{1}{3},-\frac{1}{2}\right)\). The radius is \(\sqrt{8}=2 \sqrt{2}\).
Write the equation for the following circle.
\((x-1)^{2}+(y+2)^{2}=4\)
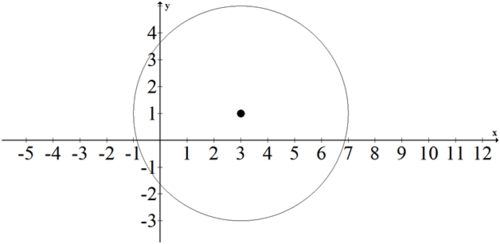
Write the equation of the following circle.
The center of the circle is at (3,1) and the radius of the circle is \(r=4\). The equation is \((x-3)^{2}+(y-1)^{2}=16\)
Graph the following conics:
1. \((x+4)^{2}+(y-3)^{2}=1\)
2. \((x-7)^{2}+(y+1)^{2}=4\)
3. \((y+2)^{2}+(x-1)^{2}=9\)
4. \(x^{2}+(y-5)^{2}=8\)
5. \((x-2)^{2}+y^{2}=16\)
Translate the following conics from standard form to graphing form.
6. \(x^{2}-4 x+y^{2}+10 y+18=0\)
7. \(x^{2}+2 x+y^{2}-8 y+1=0\)
8. \(x^{2}-6 x+y^{2}-4 y+12=0\)
9. \(x^{2}+2 x+y^{2}+14 y+25=0\)
10. \(x^{2}-2 x+y^{2}-2 y=0\)
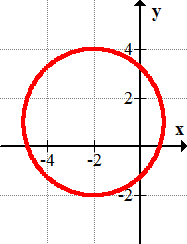
Write the equations for the following circles.
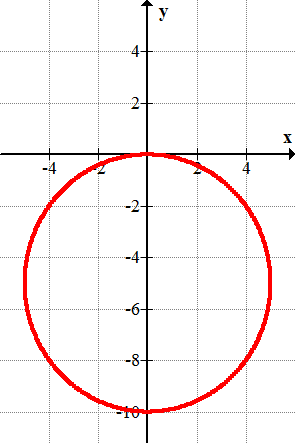
11.
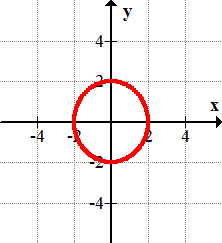
12.
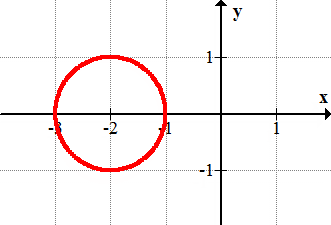
13.
14.
15.
