2.9.3: Effects on Box-and-Whisker Plots
- Page ID
- 5780
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Effect of Outliers and Changing Units
Here is some data for reservoirs in California (the names of the lakes and reservoirs have been omitted):
80, 83, 77, 95, 85, 74, 34, 68, 90, 82, 75
At first glance, the 34 should stand out. It appears as if this point is significantly different from the rest of the data. What effect does this one point have on a box-and-whisker plot?
Investigating Box-and-Whisker Plots
Use a graphing calculator to investigate the box-and-whisker plot for the California reservoir data.
Enter your data into a list as we have done before, and then choose a plot. Under 'Type', you will notice what looks like two different box and whisker plots. For now choose the second one (even though it appears on the second line, you must press the right arrow to select these plots).
Setting a window is not as important for a box plot, so we will use the calculator's ability to automatically scale a window to our data by pressing [ZOOM] and selecting '9:Zoom Stat'.
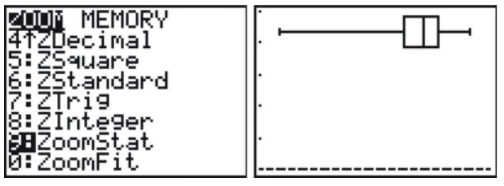
Outliers in Box-and-Whisker Plots
While box plots give us a nice summary of the important features of a distribution, we lose the ability to identify individual points. The left whisker is elongated, but if we did not have the data, we would not know if all the points in that section of the data were spread out, or if it were just the result of the one outlier. It is more typical to use a modified box plot. This box plot will show an outlier as a single, disconnected point and will stop the whisker at the previous point.
Creating Modified Box Plots
Go back and change your plot to the first box plot option, which is the modified box plot, and then graph it.
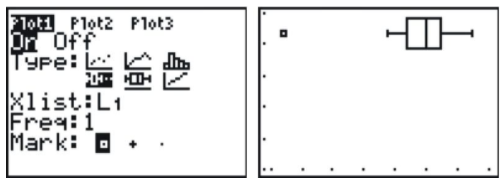
Notice that without the outlier, the distribution is really roughly symmetric.
Calculating Outliers
The California reservoir data set had one obvious outlier, but when is a point far enough away to be called an outlier? We need a standard accepted practice for defining an outlier in a box plot. This rather arbitrary definition is that any point that is more than 1.5 times the interquartile range will be considered an outlier. Because the IQR is the same as the length of the box, any point that is more than one-and-a-half box lengths from either quartile is plotted as an outlier.
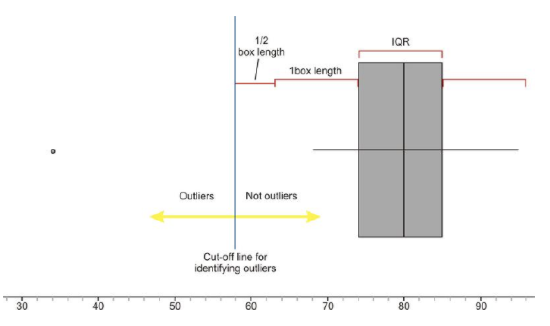
A common misconception of students is that you stop the whisker at this boundary line. In fact, the last point on the whisker that is not an outlier is where the whisker stops.
Determining Outliers
The calculations for determining the outlier in this case are as follows:
Lower Quartile: 74
Upper Quartile: 85
Interquartile range (IQR):85−74=11
1.5∗IQR=16.5
Cut-off for outliers in left whisker: 74−16.5=57.5. Thus, any value less than 57.5 is considered an outlier.
Notice that we did not even bother to test the calculation on the right whisker, because it should be obvious from a quick visual inspection that there are no points that are farther than even one box length away from the upper quartile.
If you press [TRACE] and use the left or right arrows, the calculator will trace the values of the five-number summary, as well as the outlier.
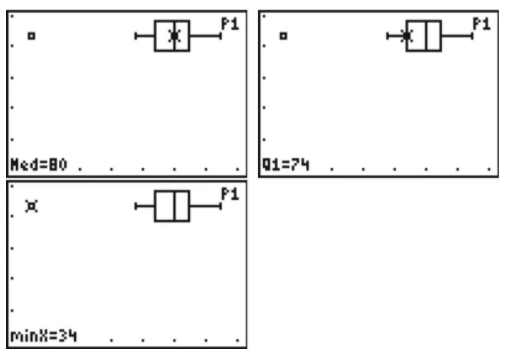
There is only one outlier, and that is the data point 34.
The Effects of Changing Units on Shape, Center, and Spread
In a previous section, we looked at data for the materials in a typical desktop computer.
| Material | Kilograms |
|---|---|
| Plastics | 6.21 |
| Lead | 1.71 |
| Aluminum | 3.83 |
| Iron | 5.54 |
| Copper | 2.12 |
| Tin | 0.27 |
| Zinc | 0.60 |
| Nickel | 0.23 |
| Barium | 0.05 |
| Other elements and chemicals | 6.44 |
Here is the data set given in pounds. The weight of each in kilograms was multiplied by 2.2.
| Material | Pounds |
|---|---|
| Plastics | 13.7 |
| Lead | 3.8 |
| Aluminum | 8.4 |
| Iron | 12.2 |
| Copper | 4.7 |
| Tin | 0.6 |
| Zinc | 1.3 |
| Nickel | 0.5 |
| Barium | 0.1 |
| Other elements and chemicals | 14.2 |
What effect does this conversion from kilograms to pounds have on some of the statistics we use to summarize data?
Determining the Effect of Conversions on the Mean, Standard Deviation, and Box Plots
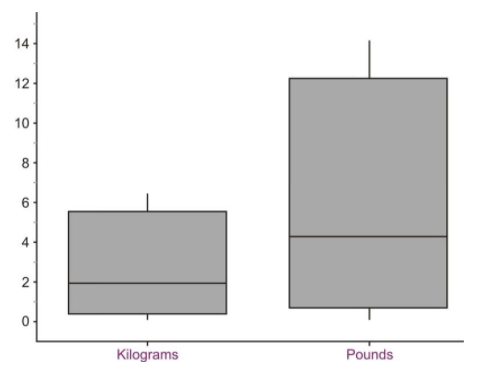
When all values are multiplied by a factor of 2.2, the calculation of the mean is also multiplied by 2.2, so the center of the distribution would be increased by the same factor. Similarly, calculations of the range, interquartile range, and standard deviation will also be increased by the same factor. In other words, the center and the measures of spread will increase proportionally.
Note: This is easier to convince yourself when you are working with actual numbers. Suppose that your mean is 20, and that two of the data values in your distribution are 21 and 23. If you multiply 21 and 23 by 2, you get 42 and 46, and your mean also changes by a factor of 2 and is now 40. Before your deviations were 21−20=1 and 23−20=3, but now, your deviations are 42−40=2 and 46−40=6, so your deviations are getting twice as big as well.
Since each number in the data set is doubled, the five-number summary is doubled, which makes the values in the box plot doubled. This results in the graph maintaining the same shape, but being stretched out, or elongated. Here are the side-by-side box plots for both distributions showing the effects of changing units.
Examples
The following examples use the data set below:
111, 122, 133, 149, 126, 117, 101, 121
Example 1
Find the median value for the data set.
To find the median, put the data in order and find the middle data point. That is, find the data point that has 50% of the data below it and 50% of the data above it. The data in order: 101, 111, 117, 121, 122, 126, 133, 149. There are 8 data points. The median would be between the 4th and 5th data points. In this case, the median is 121.5. Note that the median does not have to be a data point.
Example 2
Find the values of the upper and lower quartiles.
The lower quartile is the lower fourth of the data and the upper quartile separates the upper fourth of the data from the lower 75% of the data. In this data set the lower quartile is 114 and the upper quartile is 128.5
Example 3
Find the value of the interquartile range (IQR).
The interquartile range (IQR) is 128.5 – 114 = 14.5
Example 4
Identify any outliers in the data set.
Use the 1.5IQR rule: 1.5*IQR = 21.75. 128.5 + 21.75 = 150.25. Any value greater than 150.25 would be an outlier. There are no such values in this data set. 114 – 21.75 = 92.25. Any value less than 92.25 would be considered an outlier. There are no such values in this dataset.
Example 5
Draw a box and whisker plot for this data.
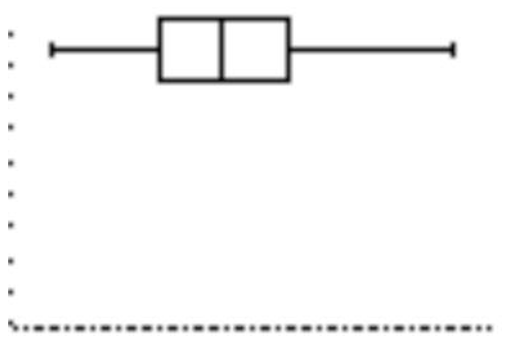
Review
For 1-7, use the table below, which contains recent data on the average price of a gallon of gasoline for states that share a border crossing into Canada.
- Find the five-number summary for this data.
- Show all work to test for outliers.
- Graph the box-and-whisker plot for this data.
- Canadian gasoline is sold in liters. Suppose a Canadian crossed the border into one of these states and wanted to compare the cost of gasoline. There are 3.7854 liters in a gallon. If we were to convert the distribution to liters, describe the resulting shape, center, and spread of the new distribution.
- Complete the following table. Convert to cost per liter by dividing by 3.7854, and then graph the resulting box plot.
- Look up the current data and compare that distribution with the data presented here.
- Find the exchange rate for Canadian dollars and convert the prices into American dollars.
| State | Average Price of a Gallon of Gasoline (US$) | Average Price of a Liter of Gasoline (US$) |
|---|---|---|
| Alaska | 3.458 | |
| Washington | 3.528 | |
| Idaho | 3.26 | |
| Montana | 3.22 | |
| North Dakota | 3.282 | |
| Minnesota | 3.12 | |
| Michigan | 3.352 | |
| New York | 3.393 | |
| Vermont | 3.252 | |
| New Hampshire | 3.152 | |
| Maine | 3.309 |
Average Prices of a Gallon of Gasoline on March 16, 2008
Figure: Average prices of a gallon of gasoline on March 16, 2008. Source: AAA.
- What characteristics of a data set make it easier or harder to represent it using dot plots, stem-and-leaf plots, histograms, and box-and-whisker plots?
- Which plots are most useful to interpret the ideas of shape, center, and spread?
- What effects do other transformations of the data have on the shape, center, and spread?
- If the median of a distribution is less than the mean, which of the following statements is the most correct?
- The distribution is skewed left.
- The distribution is skewed right.
- There are outliers on the left side.
- There are outliers on the right side.
- (b) or (d) could be true.
- Given the following data set: 111, 122, 133, 149, 126, 117, 101, 121
- Find the median value for the data set.
- Find the values of the upper and lower quartiles.
- Find the value of the interquartile range (IQR).
- Identify any outliers in the dataset.
- Draw a box and whisker plot for this data.
Vocabulary
| Term | Definition |
|---|---|
| box- and- whisker plot | A box- and- whisker plot is a graphic display of quantitative data that demonstrates the five number summary. |
| modified box-plot | A modified box plot has whiskers that extend to the highest and lowest non-outlier value. |
Additional Resources
PLIX: Play, Learn, Interact, eXplore - Box-and-Whisker Plot: Babies in a Waiting Room
Video: Box-and-Whisker Plot

