7.3: Theoretical and Experimental Spinners
- Page ID
- 5736
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Theoretical and Experimental Spinners
The 2 types of probability are theoretical probability and experimental probability. Theoretical probability is defined as the number of desired outcomes divided by the total number of outcomes.
Theoretical Probability
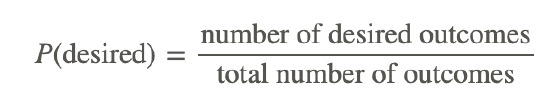
Experimental probability is, just as the name suggests, dependent on some form of data collection. To calculate the experimental probability, divide the number of times the desired outcome has occurred by the total number of trials.
Experimental Probability
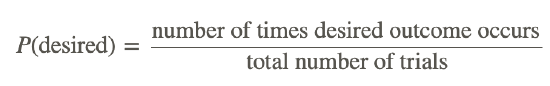
What is interesting about theoretical and experimental probabilities is that, in general, the more trials you do, the closer the experimental probability gets to the theoretical probability. We'll see this as we go through the examples.
Comparing Experimental and Theoretical Probability
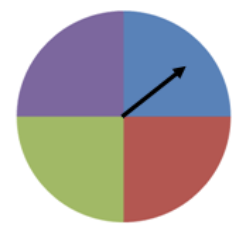
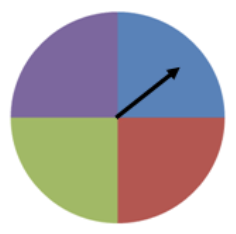
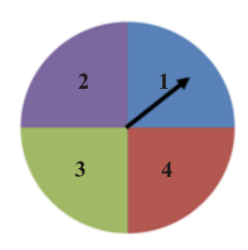
1. You are spinning a spinner like the one shown below 20 times. How many times does it land on blue? How does the experimental probability of landing on blue compare to the theoretical probability? Simulate the spinning of the spinner using technology.
On the TI-84 calculator, there are a number of possible simulations you can do. You can do a coin toss, spin a spinner, roll dice, pick marbles from a bag, or even draw cards from a deck.
After pressing ENTER, you will have the following screen appear.
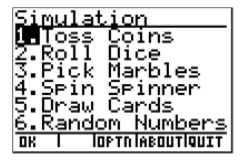
Since we're doing a spinner problem, choose Spin Spinner.
In Spin Spinner, a wheel with 4 possible outcomes is shown. You can adjust the number of spins, graph the frequency of each number, and use a table to see the number of spins for each number. We want to set this spinner to spin 20 times. Look at the keystrokes below and see how this is done.
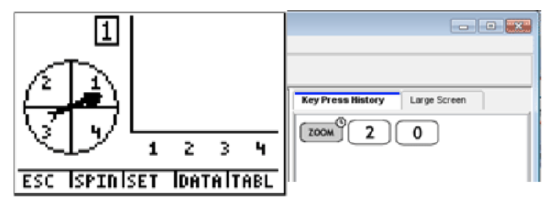
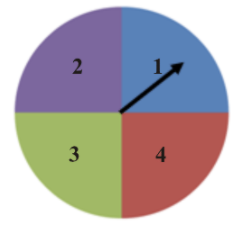
In order to match our color spinner with the one found in the calculator, you will see that we have added numbers to our spinner. This is not necessary, but it may help in the beginning to remember that 1 = blue (for this example).
Now that the spinner is set up for 20 trials, choose SPIN by pressing WINDOW
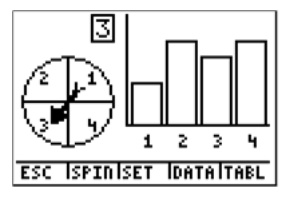
We can see the result of each trial by choosing TABL, or pressing GRAPH
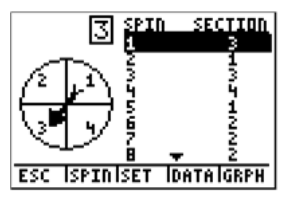
And we see the graph of the resulting table, or go back to the first screen, simply by choosing GRPH, or pressing GRAPH again.
Now, the question asks how many times we landed on blue (number 1). We can actually see how many times we landed on blue for these 20 spins. If you press the right arrow (▸), the frequency label will show you how many of the times the spinner landed on blue (number 1).
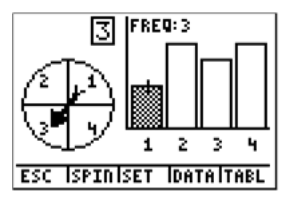
To go back to the question, how many times does the spinner land on blue if it is spun 20 times? The answer is 3. To calculate the experimental probability of landing on blue, we have to divide by the total number of spins.
P(blue)=3/20=0.15
Therefore, for this experiment, the experimental probability of landing on blue with 20 spins is 15%.
Now let's calculate the theoretical probability. We know that the spinner has 4 equal parts (blue, purple, green, and red). In a single trial, we can assume that:
P(blue)=1/4=0.25
Therefore, for our spinner example, the theoretical probability of landing on blue is 0.25. Finding the theoretical probability requires no collection of data.
2. You are spinning a spinner like the one shown below 50 times. How many times does it land on blue? How about if you spin it 100 times? Does the experimental probability get closer to the theoretical probability? Simulate the spinning of the spinner using technology.
Set the spinner to spin 50 times and choose SPIN by pressing WINDOW
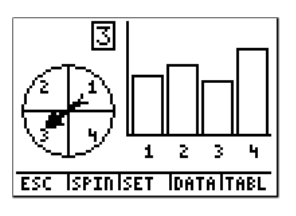
You can see the result of each trial by choosing TABL, or pressing GRAPH
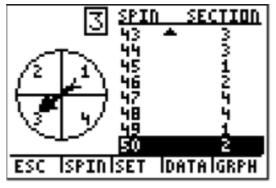
Again, we can see the graph of the resulting table, or go back to the first screen, simply by choosing GRAPH, or pressing GRAPH again.
The question asks how many times we landed on blue (number 1) for the 50 spins. Press the right arrow (▸), and the frequency label will show you how many of the times the spinner landed on blue (number 1).
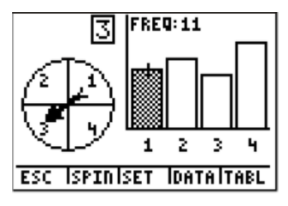
Now go back to the question. How many times does the spinner land on blue if it is spun 50 times? The answer is 11. To calculate the probability of landing on blue, we have to divide by the total number of spins.
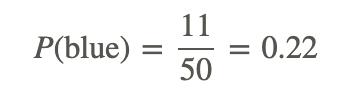
Therefore, for this experiment, the probability of landing on blue with 50 spins is 22%.
If we tried 100 trials, we would see something like the following:
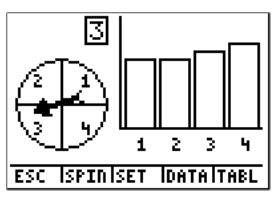
In this case, we see that the frequency of 1 is 23.
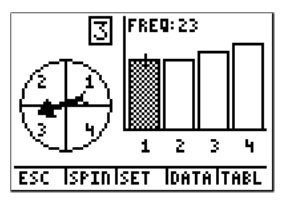
So how many times does the spinner land on blue if it is spun 100 times? The answer is 23. To calculate the probability of landing on blue in this case, we again have to divide by the total number of spins.
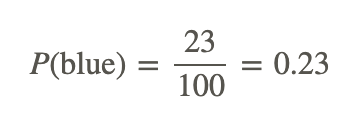
Therefore, for this experiment, the probability of landing on blue with 100 spins is 23%. You can see that as we perform more trials, we get closer to 25%, which is the theoretical probability.
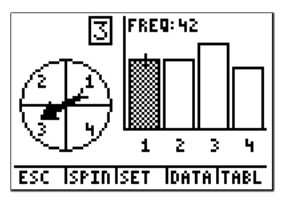
3. You are spinning a spinner like the one shown below 170 times. How many times does it land on blue? Does the experimental probability get closer to the theoretical probability? How many times do you predict we would have to spin the spinner to have the experimental probability equal the theoretical probability? Simulate the spinning of the spinner using technology.
With 170 spins, we get a frequency of 42 for blue.
The experimental probability in this case can be calculated as follows
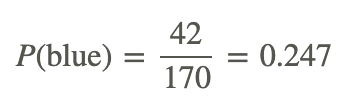
Therefore, the experimental probability is 24.7%, which is even closer to the theoretical probability of 25%. While we're getting closer to the theoretical probability, there is no number of trials that will guarantee that the experimental probability will exactly equal the theoretical probability.
Example
Example 1
You are spinning a spinner like the one shown below 500 times. How many times does it land on blue? How does the experimental probability of landing on blue compare to the theoretical probability? Simulate the spinning of the spinner using technology.
In the list of applications on the TI-84 calculator, choose Prob Sim.
After pressing ENTER, you will have the following screen appear.
Since we're doing a spinner problem, choose Spin Spinner.
In Spin Spinner, a wheel with 4 possible outcomes is shown. You can adjust the number of spins, graph the frequency of each number, and use a table to see the number of spins for each number. We want to set this spinner to spin 500 times. To do this, choose SET by pressing ZOOM, enter 500 after Trial Set, and choose OK by pressing GRAPH.
Remember that for this example, 1 = blue.
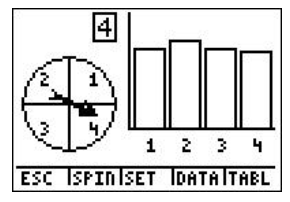
Now that the spinner is set up for 500 trials, choose SPIN by pressing WINDOW. Since we've chosen a large number of spins, the spinning may take a while!
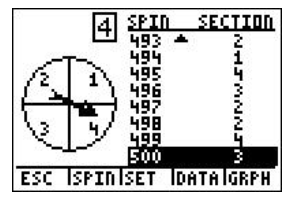
We can see the result of each trial by choosing TABL, or pressing GRAPH
And we see the graph of the resulting table, or go back to the first screen, simply by choosing GRPH, or pressing GRAPH again.
Now, the question asks how many times we landed on blue (number 1). We can actually see how many times we landed on blue for these 500 spins. If you press the right arrow (▸), the frequency label will show you how many of the times the spinner landed on blue (number 1).
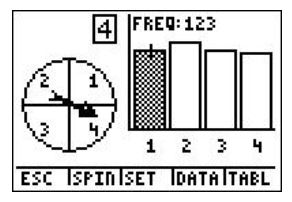
To go back to the question, how many times does the spinner land on blue if it is spun 500 times? The answer is 123. To calculate the experimental probability of landing on blue, we have to divide by the total number of spins.
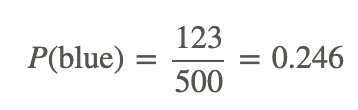
Therefore, for this experiment, the experimental probability of landing on blue with 500 spins is 24.6%.
Do you remember how to calculate the theoretical probability from Example A? We know that the spinner has 4 equal parts (blue, purple, green, and red). In a single trial, we can assume that:
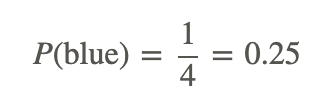
Therefore, for our spinner example, the theoretical probability of landing on blue is 0.25. As we pointed out in Example A, finding the theoretical probability requires no collection of data. It's also worth mentioning that our experimental probability was slightly farther away from the theoretical probability with 500 spins that it was with 170 spins in Example C. While, in general, increasing the number of spins will produce an experimental probability that is closer to the theoretical probability, as we've just seen, this is not always the case!
Review
- Based on what you know about probabilities, write definitions for theoretical and experimental probability.
- .
- What is the difference between theoretical and experimental probability?
- As you add more data, do your experimental probabilities get closer to or further away from your theoretical probabilities?
- Is spinning 1 spinner 100 times the same as spinning 100 spinners 1 time? Why or why not?
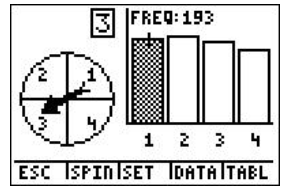
A spinner was spun 750 times using Spin Spinner on the TI-84 calculator, with 1 representing blue, 2 representing purple, 3 representing green, and 4 representing red as shown:
3. According to the following screen, what was the experimental probability of landing on blue?
4. According to the following screen, what was the experimental probability of landing on purple?
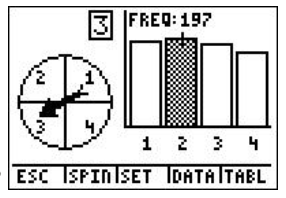
5. According to the following screen, what was the experimental probability of landing on green?
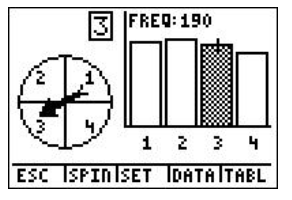
6. According to the following screen, what was the experimental probability of landing on red?
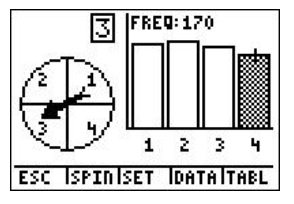
A spinner was spun 900 times using Spin Spinner on the TI-84 calculator, with 1 representing blue, 2 representing purple, 3 representing green, and 4 representing red as shown:
7. According to the following screen, what was the experimental probability of landing on blue?
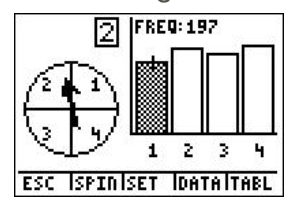
8. According to the following screen, what was the experimental probability of landing on purple?
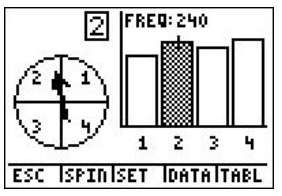
9. According to the following screen, what was the experimental probability of landing on green?
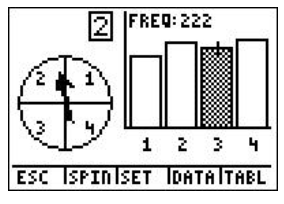
10. According to the following screen, what was the experimental probability of landing on red?
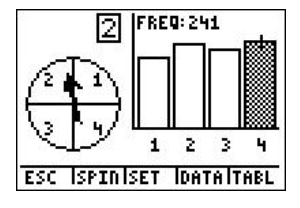
Vocabulary
| Term | Definition |
|---|---|
| experimental probability | Experimental (empirical) probability is the actual probability of an event resulting from an experiment. |
| theoretical probability | Theoretical probability is the probability ration of the number of favourable outcomes divided by the number of possible outcomes. |
Additional Resources
Video: Theoretical and Experimental Spinners Principles
Activities: Theoretical and Experimental Coin Tosses Discussion Questions
Lesson Plans: Using Technology to Find Probability Distributions, Spinning a Spinner Lesson Plan
Practice: Theoretical and Experimental Spinners
Real World: Theoretical and Experimental Probability

