2.1.4: COS
- Page ID
- 4217
Determine cosine given side lengths
Understanding Cosines

Roger has placed a ladder that is 12 feet in length against the side of the house such that the foot of the ladder is 5 feet from the base of the house. As Roger prepares to climb the ladder to clean the rain gutters of the house, his neighbor yells to him, “You had better adjust that ladder. The angle between the ladder and the ground has to be less than \(75^{\circ}\).”
Roger stepped back and looked at the position of the ladder. “He could be right,” thought Roger. “I’ve got to figure out the size of that angle before I climb up that ladder.”
How can Roger calculate the measure of the angle?
In this concept, you will learn to understand the trigonometric ratio Cosine.
Cosine
Trigonometry is a branch of mathematics used to determine the lengths of sides and the measure of angles with great accuracy. A ratio of the lengths of the sides of a right triangle is called a trigonometric ratio. The ratio of the length of the side alongside the reference angle to the length of the hypotenuse is known as the Cosine ratio. An acute angle of a right triangle is formed by the hypotenuse and one of the legs of the triangle. This leg is called the adjacent side of the reference angle. The Cosine ratio is the ratio of the adjacent side to the hypotenuse.
In each given diagram, label each side of the right triangle as the:
Hypotenuse (H); Side Opposite reference angle (O); Side Adjacent to reference angle (A).
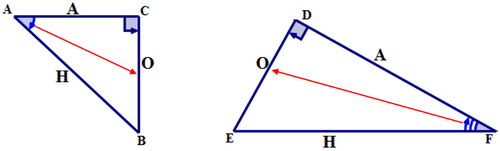
The Cosine ratio for the first triangle can be written in words as:
cosine of \(\angle A=\dfrac{\text{side adjacent }\angle A}{\text{hypotenuse}}\) Or in a shortened form as cosine of \(\angle A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
The cosine ratio for the first triangle can be written in symbols as:
\(\cos A=\dfrac{AC}{AB}\)
The Cosine ratio for the second triangle can be written in words as:
cosine of \(\angle F = \dfrac{\text{side adjacent }\angle F}{\text{hypotenuse}}\) Or in a shortened form as cosine of \(\angle F=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
The Cosine ratio for the second triangle can be written in symbols as:
\(\cos F=\dfrac{DF}{EF}\)
Let’s determine the value for the cosine ratio of each of the acute angles using the following right triangle. Express the cosine ratio in words and symbols. Then, using the values on the corresponding sides, replace the symbols with the numbers and express the ratio first as a fraction and then as a decimal rounded to the nearest ten thousandth (four places after the decimal).
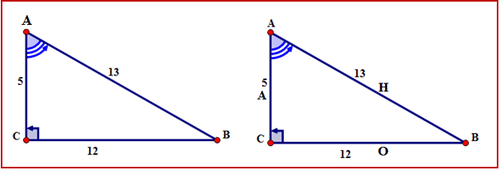
\(\Delta ABC\) with \(\angle A\) as the reference angle.
First, name the sides of the triangle.
The hypotenuse is across from the right angle. The opposite side is across from \angle A. The side alongside \angle A is the adjacent. The sides are labeled with the letters H, O, A respectively.
Next, write the cosine ratio for \(\angle A\) in all of the required forms.
Words:
cosine of \(\angle A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Symbols:
\(\cos A=\dfrac{AC}{AB}\)
Fraction:
\(\cos A=\dfrac{5}{13}\)
Decimal:
\(\cos A=0.3846\)
\(\Delta ABC\) with \(\angle B\) as the reference angle.
Notice that the locations of the opposite and adjacent sides have changed from where they were when \(\angle A\) was the reference angle.
First, name the sides of the triangle.
The hypotenuse is across from the right angle. The opposite side is across from \(\angle B\). The side alongside \(\angle B\) is the adjacent. The sides are labeled with the letters H, O, A respectively.
Next, write the cosine ratio for \(\angle B\) in all of the required forms.
Words:
cosine of \(\angle B=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Symbols:
\(\cos B=\dfrac{BC}{AB}\)
Fraction:
\(\cos B=\dfrac{12}{13}\)
Decimal:
\(\cos B=0.9231\)
If \(\cos A=0.3846\), then the measure of \(\angle A\) can be found using the inverse cosine function on the TI- calculator.
First, follow the Key Press History below to calculate the measure of \(\angle A\).
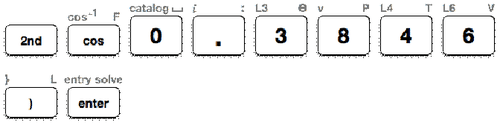
Next, look at the calculator screen to see the measure of \(\angle A\).
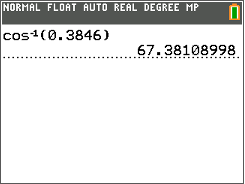
Then, write the measure of \(\angle A\) to the nearest tenth.
\(\angle A=67.4^{\circ}\)
The answer is \(67.4^{\circ}\)
Earlier, you were given a problem about Roger and the ladder. He needs to figure out the angle the ladder makes with the ground.
How can Roger figure out the measure of the angle?
Solution
He can use the cosine ratio.
First, draw and label a right triangle to model the problem.
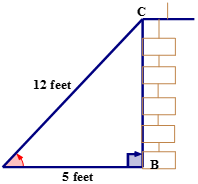
Next, name the sides of the triangle.
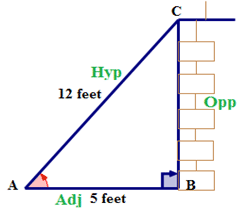
Next, write the cosine ratio in words.
\(\cos A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Next, write the ratio using symbols.
\(\cos A=\dfrac{AB}{AC}\)
Next, express the ratio as a fraction using the values of the corresponding sides.
\(\cos A=\dfrac{5}{12}\)
Next, express the ratio as a decimal rounded to four places after the decimal.
\(\cos A=0.4167\)
Next, use the inverse cosine function (cos−1) on the TI calculator to find the measure of \(\angle A\).
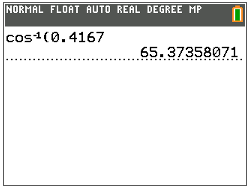
Then, write the measure of \(\angle A\) to the nearest tenth.
\(\angle A=65.4^{\circ}\)
The answer is \(65.4^{\circ}\)
The measure of \(\angle A\) is \(65.4^{\circ}\). It is less than \(75^{\circ}\) so Roger can repair the rain gutters.
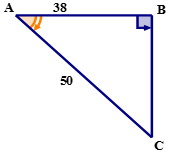
Use the cosine ratio to calculate the measure of \(\angle A\) to the nearest tenth.
Solution
First, using the reference angle name the sides of the triangle.
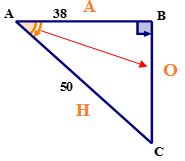
Next, write the cosine ratio in words.
\(\cos A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Next, write the ratio using symbols.
\(\cos A=\dfrac{AB}{AC}\)
Next, express the ratio as a fraction using the values of the corresponding sides.
\(\cos A=\dfrac{38}{50}\)
Next, express the ratio as a decimal rounded to four places after the decimal.
\(\cos A=0.76\)
The decimal terminated. You could write the decimal as 0.7600 but this is not necessary.
Next, use the inverse cosine function (\(\cos^{−1}\)) on the TI calculator to find the measure of \(\angle A\).
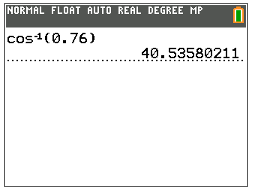
Then, write the value of \(\angle A\) to the nearest tenth.
\(\angle A=40.5^{\circ}\)
The answer is \(40.5^{\circ}\)
If \(\cos B=0.7984\), what is the measure of \(\angle B\) to the nearest tenth.
Solution
First, use the TI-calculator to determine the measure of \(\angle B\) by using the inverse cosine function (\(\cos^{−1}) on the calculator. This function is above the cos button on the calculator. To access this function press
Next, enter the decimal 0.7984 in the parenthesis where the cursor is flashing.
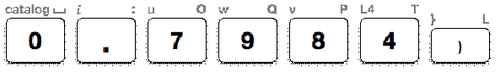
Next, press enter and the calculator screen will display the measure of the angle.

Then, write the measure of \(\angle B\) to the nearest tenth.
\(\angle B=32.0^{\circ}\).
The answer is \(32.0^{\circ}\)
For the following solution that shows using the cosine ratio to calculate the measure of \angle B, draw and label the right triangle ABC that was used to do the solution.
\(\begin{aligned}
\cos B &=\frac{\text { adjacent }}{\text { hypotenuse }} \\
\cos B &=\frac{B C}{A B} \\
\cos B &=\frac{36}{76.7} \\
\cos B &=0.4694 \\
\cos ^{-1}(\cos B) &=\cos ^{-1}(0.4694) \\
\angle B &=62.00454372 \\
\angle B &=62.0^{\circ}
\end{aligned}\)
Solution
First, write down what you know from the solution.
\(\Delta ABC\) is a right triangle.
\(\overline{BC}\) is the adjacent side of the triangle.
\(\overline{BC}\) has a length of 36.
\(\overline{AB}\) is the hypotenuse of the triangle.
\(\overline{AB}\) has a length of 76.7.
\(\angle B\) is the reference angle.
Next, use the information you have written down to draw and label the triangle.
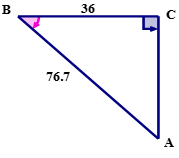
The above triangle represents the problem.
For the given right triangle, use the cosine ratio to calculate the measure of \(\angle A\) to the nearest tenth.
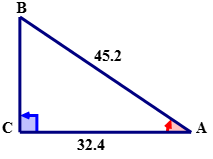
Solution
First, using the reference angle name the sides of the triangle.
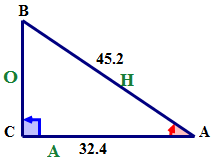
Next, write the cosine ratio in words.
\(\cos A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Next, write the ratio using symbols.
\(\cos A=\dfrac{AC}{AB}\)
Next, express the ratio as a fraction using the values of the corresponding sides.
\(\cos A=\dfrac{32.4}{45.2}\)
Next, express the ratio as a decimal rounded to four places after the decimal.
\(\cos A=0.7168\)
Next, use the inverse cosine function (\(\cos^{−1}\)) on the TI calculator to find the measure of \(\angle A\).

Then, write the measure of \(\angle A\) to the nearest tenth.
\(\angle A=44.2^{\circ}\).
The answer is \(44.2^{\circ}\)
Review
Solve each problem.
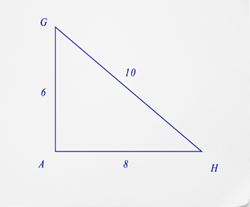
- What is the cosine of \(\angle G\)?
- What is the cosine of \(\angle H\)?
- How do you identify a cosine?
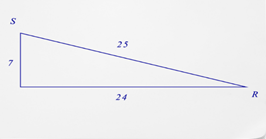
4. What is the cosine of \(\angle R\)?
5. What is the cosine of \(\angle S\)?
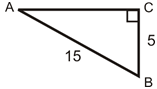
- What is the cosine of \(\angle A\)?
- What is the cosine of \(\angle B\)?
- What is the length of the missing side rounded to the nearest hundredth?
Answer each of the following questions.
- Is the cosine related to an angle?
- Do you need to know side lengths of a triangle to write a cosine?
- Which side lengths do you need?
- If the cosine was \(\dfrac{5}{20}\) what would the numerical value of the cosine be?
- If the cosine was \(\dfrac{5}{25}\) what would the numerical value of the cosine be?
- If the cosine was \(\dfrac{3}{33}\) what would the numerical value of the cosine be?
- If the cosine was \(\dfrac{12}{14}\) what would the numerical value of the cosine be?
Review (Answers)
To see the Review answers, open this PDF file and look for section 7.14.
Vocabulary
| Term | Definition |
|---|---|
| cosine | The cosine of an angle in a right triangle is a value found by dividing the length of the side adjacent the given angle by the length of the hypotenuse. |
| Trigonometric Ratios | Ratios that help us to understand the relationships between sides and angles of right triangles. |

