2.1.3: SIN
- Page ID
- 4215
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Trigonometric ratios based on sides of right triangles in relation to an angle.
Understanding Sines

Jacob has to string lights around the eaves of his flat-roofed shed. Since he is afraid of heights he wants to plan this endeavor very carefully. He knows that for safety reasons, a ladder should make an angle of \(75^{\circ}\) or less with the ground. If Jacob has a ladder 6.5 meters long to place against the side of the shed that is 2.5 meters high, then what angle will the ladder make with the ground? Jacob needs to be certain that the angle meets safety requirements before he puts one foot on the ladder. How can he figure out the measure of the angle between the ladder and the ground?
In this concept, you will learn to understand the trigonometric ratio of sine.
Sines
Trigonometry is a branch of mathematics used to determine the lengths of sides and the measure of angles with great accuracy. You will only consider the results obtained by using right angled triangles.
The side of a right triangle located opposite the 90^{\circ} angle is the longest side of the triangle and is called the hypotenuse. The two shorter sides of the triangle, often called legs, have specific names in reference to the location of one of the acute angles of the right triangle.

In both triangles the hypotenuse is opposite the right angle. In the first triangle the angle marked in red is called the reference angle and it is used to name the legs of the triangle. The measure of the reference angle can be given or its measure may have to be calculated. Whatever the case, one of the acute angle will be referred to in the question or problem. The side across from the reference angle is called the opposite side. The third side is called the adjacent side and it is the side of the triangle, along with the hypotenuse, that forms the reference angle.
In the second triangle the angle marked in red is called the reference angle and it is used to name the legs of this triangle. The side across from the reference angle is called the opposite side. The third side is called the adjacent side and it is the side of the triangle, along with the hypotenuse, that forms the reference angle.
The location of the hypotenuse never changes but the location of the opposite and adjacent sides depends upon which acute angle is the reference angle.
In each given diagram, label each side of the right triangle as the:
Hypotenuse (H); Side Opposite reference angle (O); Side Adjacent to reference angle (A)

A ratio of the lengths of the sides of a right triangle is called a trigonometric ratio. The ratio of the length of the side opposite the reference angle to the length of the hypotenuse is known as the sine ratio. The sine ratio is related to the reference angle of the right triangle, not to the right angle.
The sine ratio for the first triangle can be written in words as:
sine of \(\angle A=\dfrac{\text{side opposite} \angle A}{\text{hypotenuse}}\) Or in a shortened form as sine of \(\angle A=\dfrac{opposite}{hypotenuse}\)
The sine ratio for the first triangle can be written in symbols as:
\(\sin A=\dfrac{BC}{AB}\)
The sine ratio for the second triangle can be written in words as:
sine of \(\angle F=\dfrac{\text{side opposite}\angle F}{\text{hypotenuse}}\) Or in a shortened form as sine of \(\angle F=\dfrac{opposite}{hypotenuse}\)
The sine ratio for the first triangle can be written in symbols as:
\(\sin F=\dfrac{DE}{EF}\)
Let’s determine the value for the sine ratio of each of the acute angles using the following right triangle. Express the sine ratio in words and symbols. Then, using the values on the corresponding sides, replace the symbols with the numbers and express the ratio first as a fraction and then as a decimal rounded to the nearest ten thousandth (four places after the decimal).
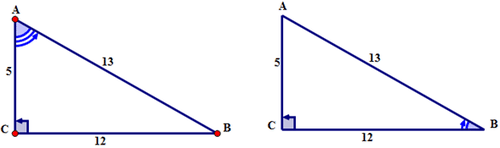
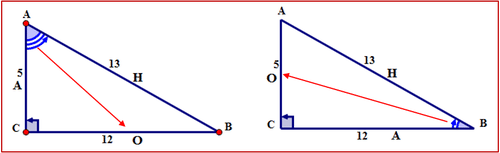
For the first triangle:
First, with the respect to the reference angle A, name the sides of the triangle.
The hypotenuse is across from the right angle. The opposite side is across from \(\angle A\). The side alongside \(\angle A\) is the adjacent. The sides are labeled with the letters H, O, A respectively.
Next, write the sine ratio for \(\angle A\) in all of the required forms.
Words:
sine of \(\angle A=\dfrac{opposite}{hypotenuse}\)
Symbols:
\(\sin A=\dfrac{BC}{AB}\)
Fraction:
\(\sin A=\dfrac{12}{13}\)
Decimal:
\(\sin A=0.9231\)
The second triangle is the first triangle with \angle B as the reference angle. Notice that the locations of the opposite and adjacent sides have changed from where they were when \angle A was the reference angle.
First, with the respect to the reference angle B, name the sides of the triangle.
The hypotenuse is across from the right angle. The opposite side is across from \(\angle B\). The side alongside \(\angle B\) is the adjacent. The sides are labeled with the letters H, O, A respectively.
Next, write the sine ratio for \(\angle B\) in all of the required forms.
Words:
sine of \(\angle B=\dfrac{opposite}{hypotenuse}\)
Symbols:
\(\sin B=\dfrac{AC}{AB}\)
Fraction:
\(\sin B=\dfrac{5}{13}\)
Decimal:
\(\sin B=0.3846\)
If sinB=0.3846, then the measure of \angle B can be found using the TI-84 calculator.
Remember you measure angles in units called degrees. Press mode and look at the screen.
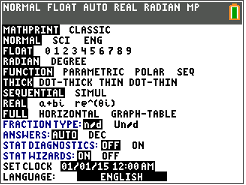
In the fourth row of the screen, DEGREE is not highlighted.
Follow the Key Press History below to put the calculator in DEGREE mode.
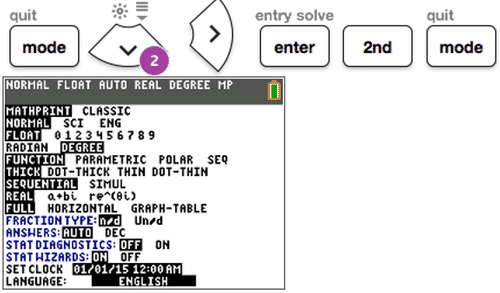 Figure \(\PageIndex{7}\)
Figure \(\PageIndex{7}\)In the fourth row of the screen, DEGREE is now highlighted.
Next, follow the Key Press History below to find the measure of \(\angle B\).
Then, look at the screen of the calculator:
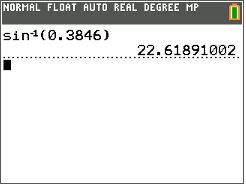
Round the measure of the angle to the nearest tenth.
\(\angle B=22.6^{\circ}\)
The answer is \(22.6^{\circ}\)
Earlier, you were given a problem about Jacob and the angle of his ladder. Jacob needs to make sure that the ladder makes an angle of less than \(75^{\circ}\) with the ground? Jacob will have to use the sine ratio to figure this out.
Solution
First, draw and label a right triangle with the information given.
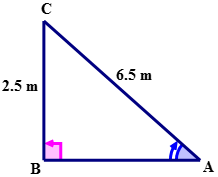
Next, name the sides of the triangle with reference to \(\angle A\).
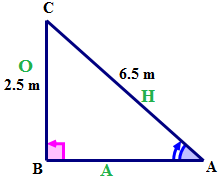
Next, express the ratio \(\sin A\) using words.
\(\sin A=\dfrac{opposite}{hypotenuse}\)
Next, express the ratio using symbols.
\(\sin A=\dfrac{BC}{AC}\)
Next, express the ratio as a fraction using the corresponding values of the sides.
\(\sin A=\dfrac{2.5}{6.5}\)
Next, express the ratio as a decimal.
\(\sin A=0.3846\)
Next, use the sin−1 function on the TI-calculator to find the measure of \angle A.
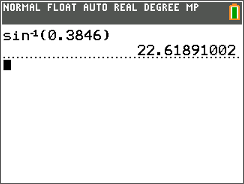
Then, write the measure of \(\angle A\) to the nearest tenth.
\(\angle A=22.6^{\circ}\)
The answer is \(22.6^{\circ}\).
It is safe for Jacob to go up the ladder.
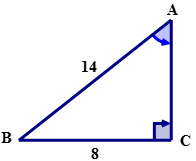
Use the sine ratio to calculate the measure of \(\angle A\) to the nearest tenth.
Solution
First, using \(\angle A\) name the sides of the triangle.
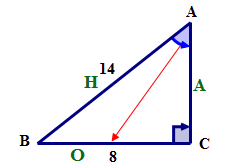
Next, write the sine ratio in words.
\(\sin A=\dfrac{opposite}{hypotenuse}\)
Next, write the ratio using symbols.
\(\sin A=\dfrac{BC}{AB}\)
Next, express the ratio as a fraction using the values of the corresponding sides.
\(\sin A=\dfrac{8}{14}\)
Next, express the ratio as a decimal rounded to four places after the decimal.
\(\sin A=0.5714\)
Then, use the inverse sine function (\(\sin^{−1}\)) on the TI calculator to find the measure of \(\angle A\).
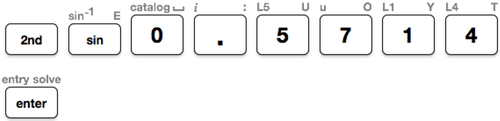
Then, look at the screen and round the measure of the angle to the nearest tenth.
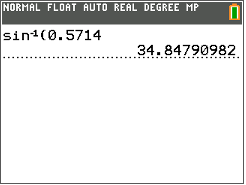
Notice, it is not necessary to close the bracket after the decimal has been entered into the calculator.
\(\angle A=34.9^{\circ}\)
The answer is \(34.9^{\circ}\)
For the following right triangle, express sinB in words, symbols, as a fraction and as a decimal.
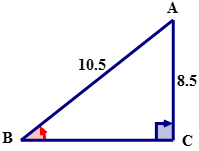
Solution
First, name the sides of the triangle using the reference angle B.
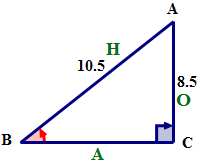
Next, express the ratio sinB using words.
\(\sin B=\dfrac{opposite}{hypotenuse}\)
Next, express the ratio using symbols.
\(\sin B=\dfrac{AC}{AB}\)
Next, express the ratio as a fraction using the corresponding values of the sides.
\(\sin B=\dfrac{8.5}{10.5}\)
Then, express the ratio as a decimal to the ten thousandth.
\(\sin B=0.8095\)
The answer is 0.8095.
If \(\sin A=0.3872\), what is the measure of \(\angle A\) to the nearest tenth.
Solution
First, use the TI-calculator and follow the key press history.
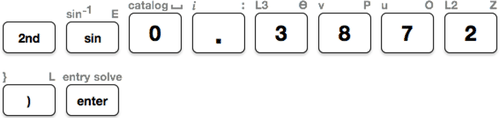
Next, look at the screen of the calculator.
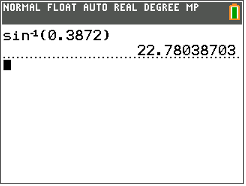
Then, write the measure of \(\angle A\) to the nearest tenth.
\(\angle A=22.8^{\circ}\)
The answer is \(22.8^{\circ}\).
Determine the measure of \angle B in the following triangle.
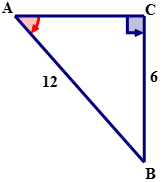
Solution
First, name the sides of the triangle.
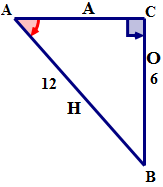
Next, express the ratio sin A using words.
\(sin A=\dfrac{opposite }{hypotenuse}\)
Next, express the ratio using symbols.
\(\sin A=\dfrac{BC}{AB}\)
Next, express the ratio as a fraction using the corresponding values of the sides.
\(\sin A=\dfrac{6}{12}\)
Next, express the ratio as a decimal.
\(\sin A=0.5\)
Next, use the sin−1 function on the TI-calculator to find the measure of \(\angle A\).
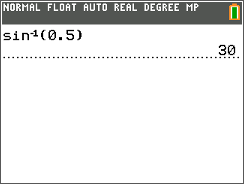
Then, write the measure of \(\angle A\).
\(\angle A=30^{\circ}\)
The answer is \(30^{\circ}\).
Review
Solve each problem.
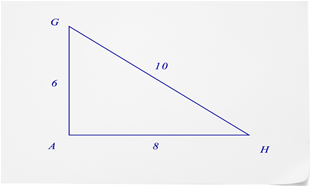
- What is the sine of \(\angle G\)?
- What is the sine of \(\angle H\)?
- Can you find the sine of \(\angle A\)?
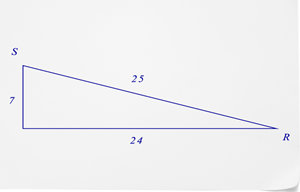
- What is the sine of \(\angle R\)?
- What is the sine of \(\angle S\)?
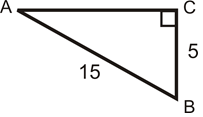
- What is the sine of \(\angle A\)?
- What is the sine of \(\angle B\)?
- What is the length of the missing side rounded to the nearest hundredth?
Answer each question true or false.
- You can use the Pythagorean Theorem to find the length of a missing side in a right triangle.
- A right triangle must have a 90 degree angle.
- The sine ratio is the hypotenuse over the opposite side.
- If you know only side length, then you can figure out all the side lengths.
- Sine ratio has to do with side lengths.
- The hypotenuse is always opposite the right angle.
- You must be given all three side lengths to figure out the sine ratio.
Review (Answers)
To see the Review answers, open this PDF file and look for section 7.13.
Vocabulary
| Term | Definition |
|---|---|
| sine | The sine of an angle in a right triangle is a value found by dividing the length of the side opposite the given angle by the length of the hypotenuse. |
| Trigonometric Ratios | Ratios that help us to understand the relationships between sides and angles of right triangles. |
Additional Resources
Video: Introduction to Trigonometric Functions Using Triangles
Activities: Trigonometric Ratios with a Calculator Discussion Questions
Practice: Calculator Trig Functions
Real World: Sine Cosine Tangent

