2.1.5: Sine and Cosine of Complementary Angles

Last updated
Save as PDF

Page ID: 4216

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Sine of an angle equals the cosine of its complement.

\(\Delta ABC\) is a right triangle with \(m\angle C=90^{\circ}\) and \(\sin A=k\). What is \(\cos B\)?

Sine and Cosine of Complementary Angles

Recall that the sine and cosine of angles are ratios of pairs of sides in right triangles.

The sine of an angle in a right triangle is the ratio of the side opposite the angle to the hypotenuse.
The cosine of an angle in a right triangle is the ratio of the side adjacent to the angle to the hypotenuse.

In the problems below, you will explore how the sine and cosine of the angles in a right triangle are related.

Let's take a look at a few example problems.

1. Consider the right triangle below. Find the sine and cosine of angles A and B in terms of a,b, and c. What do you notice?

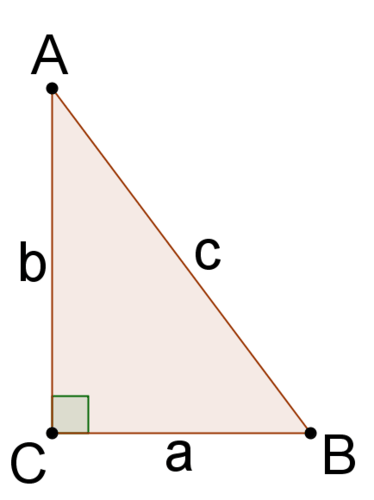
\(\sin A=\dfrac{a}{c}\), \(\sin B=\dfrac{b}{c}\), \(\cos A=\dfrac{b}{c}\), \(\cos B=\dfrac{a}{c}\) Note that \(\sin A=\cos B\) and \(\sin B=\cos A\).

2. Consider the triangle from the previous problem. How is \(\angle A\) related to \(\angle B\)?

The sum of the measures of the three angles in a triangle is \(180^{\circ}\). This means that \(m\angle A+m\angle B+m\angle C=180^{\circ}\). \(\angle C\) is a right angle so \(m\angle C=90^{\circ}\). Therefore, \(m\angle A+m\angle B=90^{\circ}\). Angles A and B are complementary angles because their sum is \(90^{\circ}\).

In #1 you saw that \(\sin A=\cos B\) and \(\sin B=\cos A\). This means that the sine and cosine of complementary angles are equal.

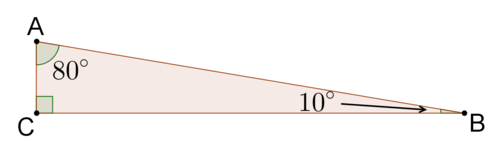
3. Find \(80^{\circ}\) and \(\cos 10^{\circ}\). Explain the result.

\(\sin 80^{\circ}\approx 0.985\) and \(\cos 10^{\circ}\approx 0.985\). \(\sin 80^{\circ}=\cos 10^{\circ}\) because \(80^{\circ}\) and \(10^{\circ}\) are complementary angle measures. \(\sin 80^{\circ}\) and \(\cos 10^{\circ}\) are the ratios of the same sides of a right triangle, as shown below.

Example \(\PageIndex{1}\)

Earlier, you were asked what is \(\cos B\).

\(\Delta ABC\) is a right triangle with \(m\angle C=90^{\circ}\) and \(\sin A=k\). What is \(\cos B\)?

Solution

\(\angle A\) and \(\angle B\) are complementary because they are the two non-right angles of a right triangle. This means that \(\sin A=\cos B\) and \(\sin B=\cos A\). If \(\sin A=k\), then \(\cos B=k\) as well.

Example \(\PageIndex{2}\)

If \(\sin 30^{\circ}=\dfrac{1}{2}\), \(\cos\stackrel?{=}\dfrac{1}{2}\).

Solution

The sine and cosine of complementary angles are equal. \(90^{\circ}−30^{\circ}=60^{\circ}\) is complementary to \(30^{\circ}\). Therefore, \(\cos 60^{\circ}=\dfrac{1}{2}\).

Example \(\PageIndex{3}\)

Consider the right triangle below. Find \(\tan A\) and \(\tan B\).

Solution

\(\tan A=\dfrac{a}{b}\) and \(\tan B=\dfrac{b}{a}\).

Example \(\PageIndex{4}\)

In general, what is the relationship between the tangents of complementary angles?

Solution

In general, the tangents of complementary angles are reciprocals.

Review

1. How are the two non-right angles in a right triangle related? Explain.

2. How are the sine and cosine of complementary angles related? Explain.

3. How are the tangents of complementary angles related? Explain.

Let A and B be the two non-right angles in a right triangle.

4. If \(\tan A=\dfrac{1}{2}\), what is \(\tan B\)?

5. If \(\sin A=\dfrac{7}{10}\), what is \(\cos B\)?

6. If \(\cos A=\dfrac{1}{4}\) what is \(\sin B\)?

7. If \(\sin A=\dfrac{3}{5}\), \(\cos \stackrel?{=} \dfrac{3}{5}\)?

8. Simplify \(\dfrac{\sin A+\cos B}{2}\).

9. If \(\tan A=\dfrac{2}{3}\) what is \(\tan B\)?

10. If \(\tan B=\dfrac{1}{5}\), what is \(\tan A\)? Which angle is bigger, \(\angle A\) or \(\angle B\)?

Solve for \(\theta\).

11. \(\cos 30^{\circ}=\sin \theta\)

12. \(\sin 75^{\circ}=\cos \theta\)

13. \(\cos 52^{\circ}=\sin \theta\)

14. \(\sin 18^{\circ}=\cos \theta\)

15. \(\cos 49^{\circ}=\sin \theta\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 7.3.

Vocabulary

Term	Definition
Complementary angles	Complementary angles are a pair of angles with a sum of \(90^{\circ}\).
cosine	The cosine of an angle in a right triangle is a value found by dividing the length of the side adjacent the given angle by the length of the hypotenuse.
sine	The sine of an angle in a right triangle is a value found by dividing the length of the side opposite the given angle by the length of the hypotenuse.

Additional Resources

Interactive Element

Practice: Sine and Cosine of Complementary Angles