2.3.3: Angles of Rotation in Standard Positions
- Page ID
- 14352
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Counterclockwise angles beginning at the positive x-axis.
While playing a game with friends, you are using a spinner. You know that the best number to land on is 7. The spinner looks like this:
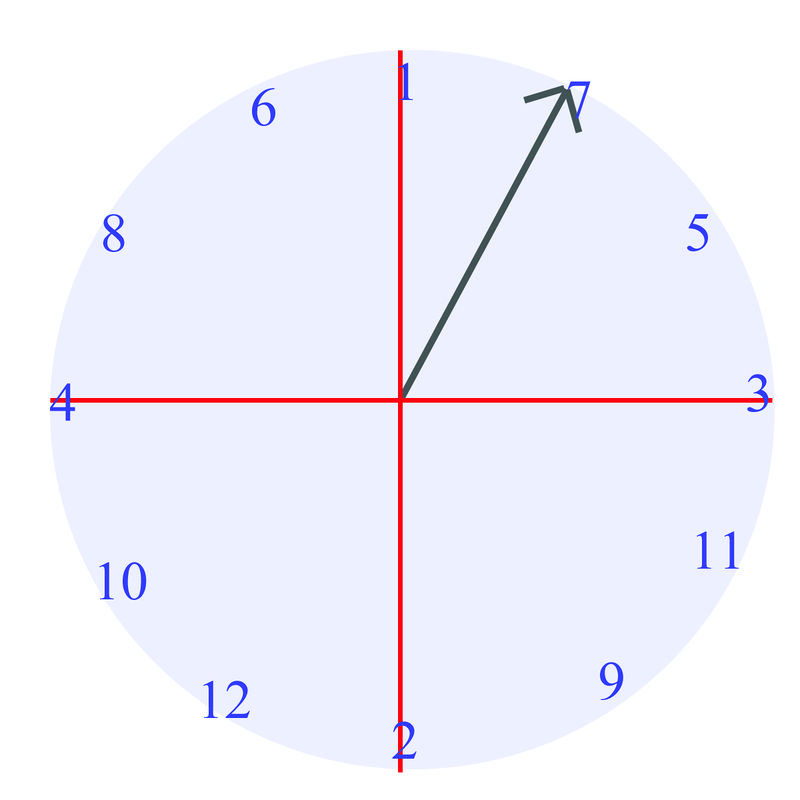
Can you determine how to represent the angle of the spinner if it lands on the 7?
Angles of Rotation in Standard Positions
Consider our game that is played with a spinner. When you spin the spinner, how far has it gone? You can answer this question in several ways. You could say something like “the spinner spun around 3 times.” This means that the spinner made 3 complete rotations, and then landed back where it started.
We can also measure the rotation in degrees. In the previous lesson we worked with angles in triangles, measured in degrees. You may recall from geometry that a full rotation is 360 degrees, usually written as \(360^{\circ}\). Half a rotation is then \(180^{\circ}\) and a quarter rotation is \(90^{\circ}\). Each of these measurements will be important in this Concept. We can use our knowledge of graphing to represent any angle. The figure below shows an angle in what is called standard position.
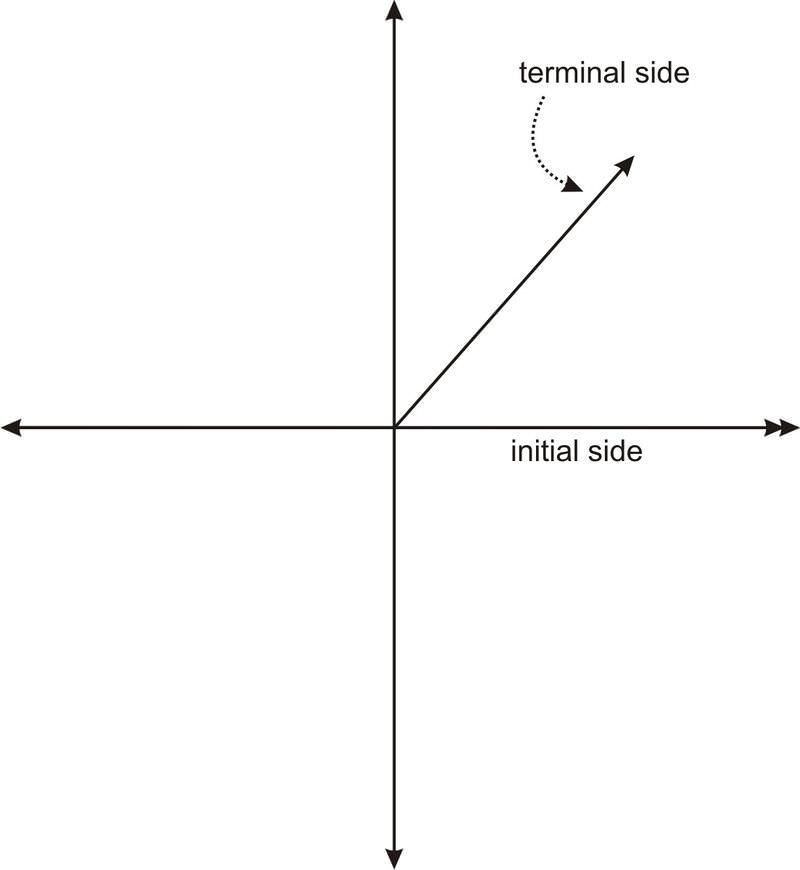
The initial side of an angle in standard position is always on the positive \(x\)−axis. The terminal side always meets the initial side at the origin. Notice that the rotation goes in a counterclockwise direction. This means that if we rotate clockwise, we will generate a negative angle. Below are several examples of angles in standard position.
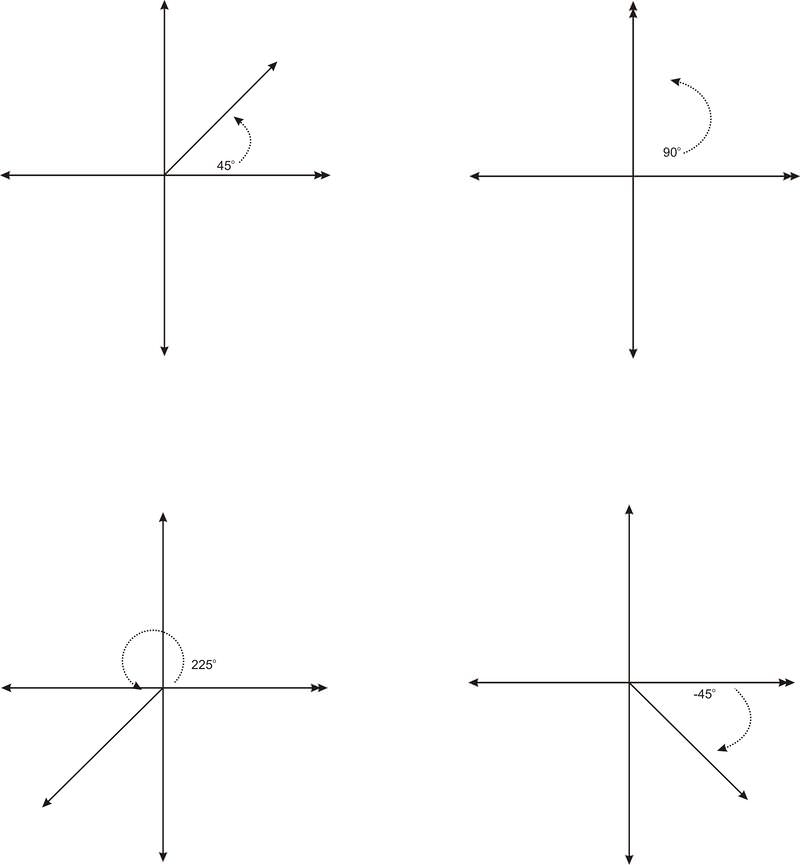
The 90 degree angle is one of four quadrantal angles. A quadrantal angle is one whose terminal side lies on an axis. Along with \(90^{\circ}\), \(0^{\circ}\), \(180^{\circ}\) and \(270^{\circ}\) are quadrantal angles.
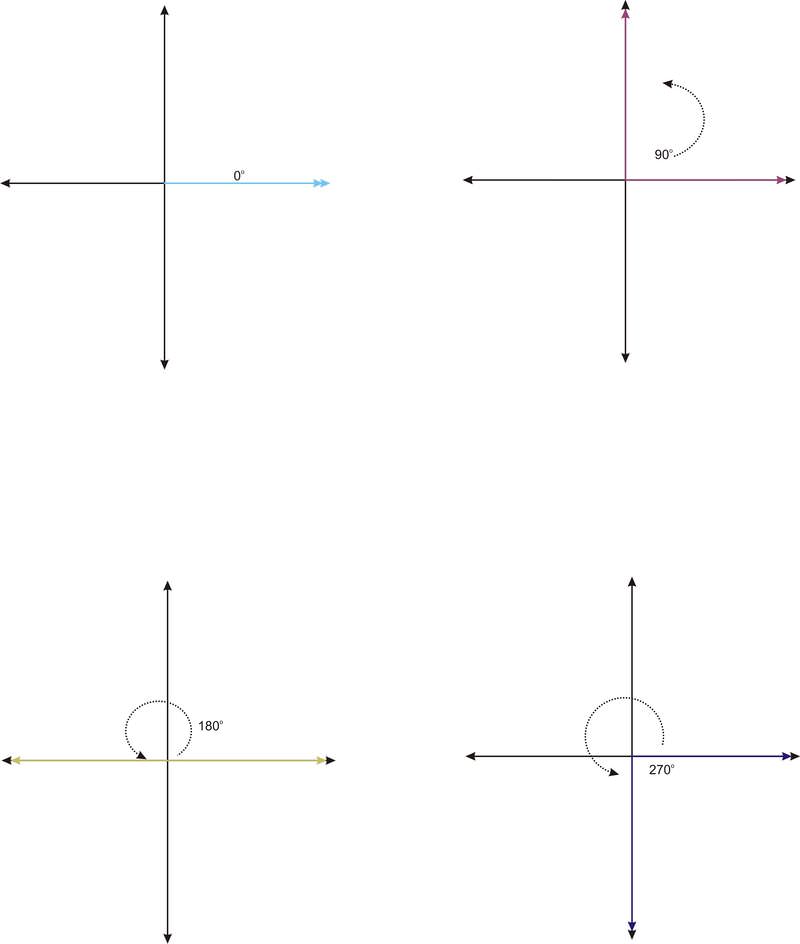
These angles are referred to as quadrantal because each angle defines a quadrant. Notice that without the arrow indicating the rotation, \(270^{\circ}\) looks as if it is a \(−90^{\circ}\), defining the fourth quadrant. Notice also that \(360^{\circ}\) would look just like \(0^{\circ}\).
Finding the Angle of Rotation
Identify what the angle is in this graph:
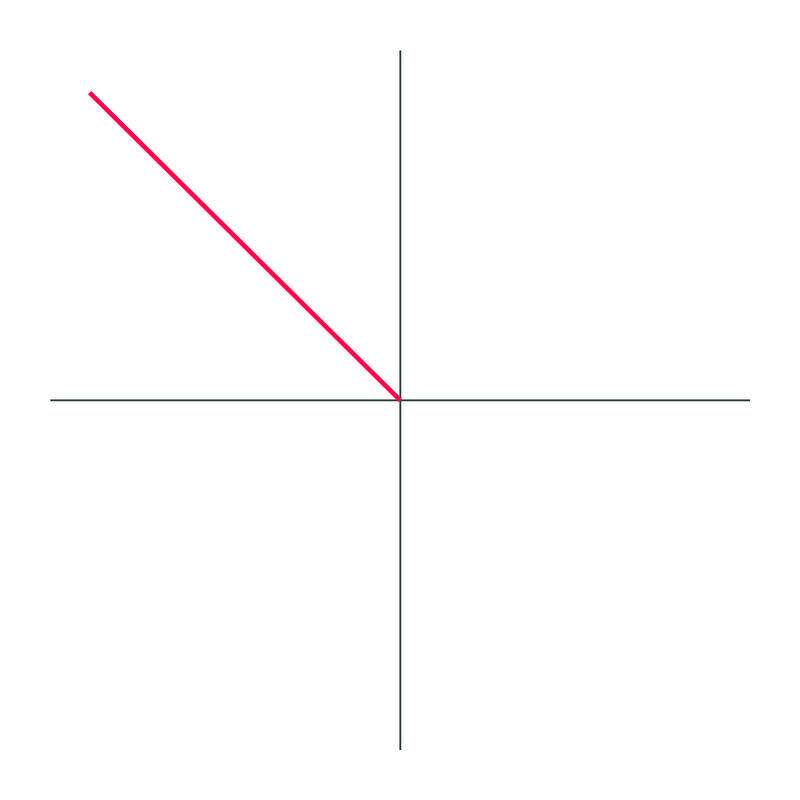
The angle drawn out is \(135^{\circ}\).
Identifying Angles
Identifying the angles within the following graphs.
1.
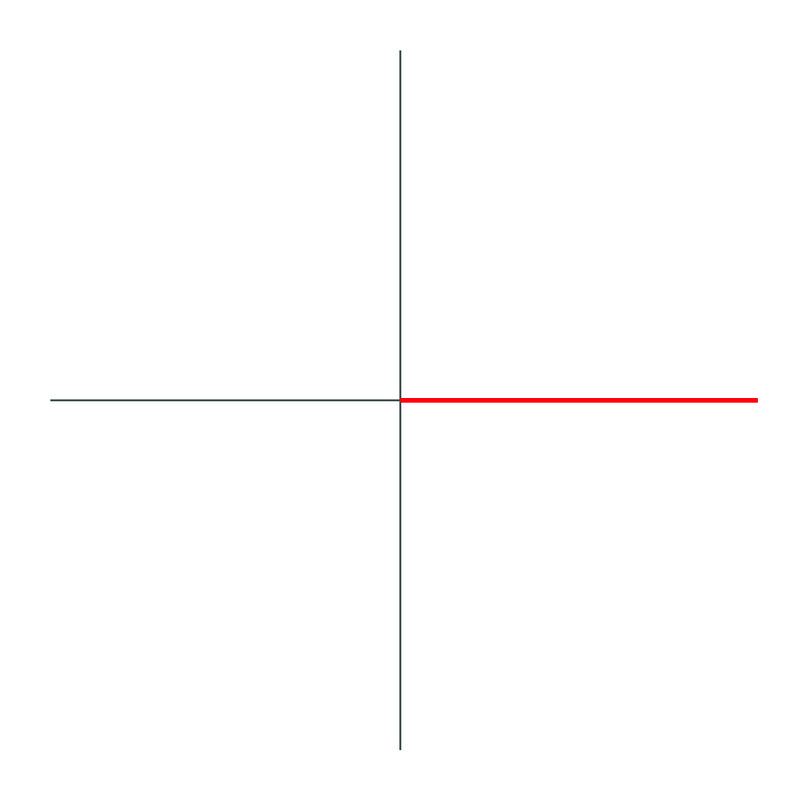
The angle drawn out is \(0^{\circ}\).
2.
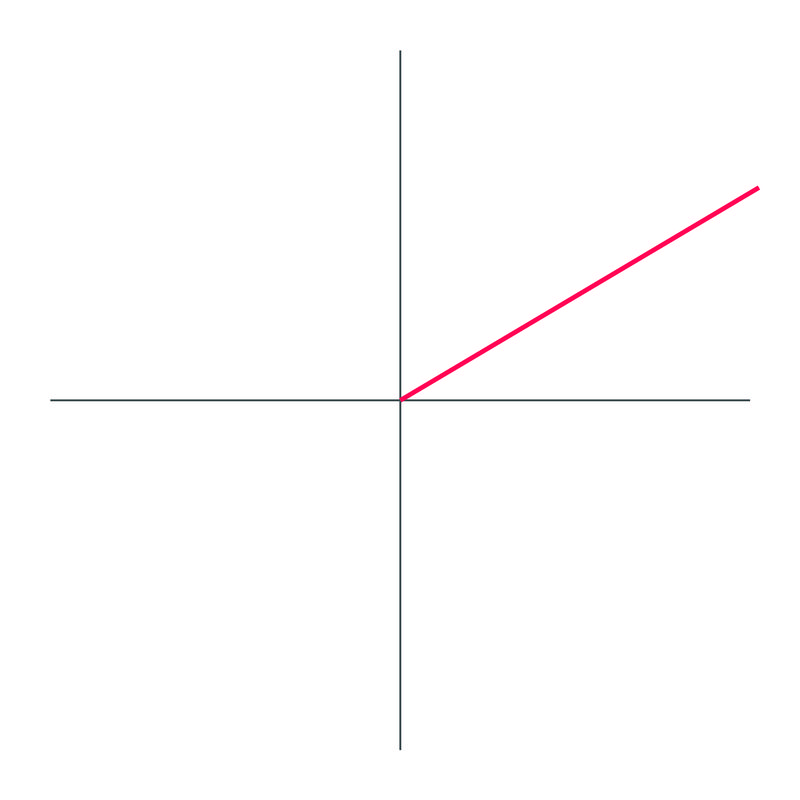
The angle drawn out is \(30^{\circ}\)
Earlier, you were asked to determine how to represent the angle of the spinner if it lands on the 7.
Solution
Since you know that the angle between the horizontal and vertical directions is \(90^{\circ}\), each number on the spinner takes up \(30^{\circ}\). Therefore, since you are on the 7, you know that you are 23 of the way to the vertical. Therefore, the angle of the spinner when it lands on 7 is \(60^{\circ}\).
Identify what the angle is in this graph, using negative angles:
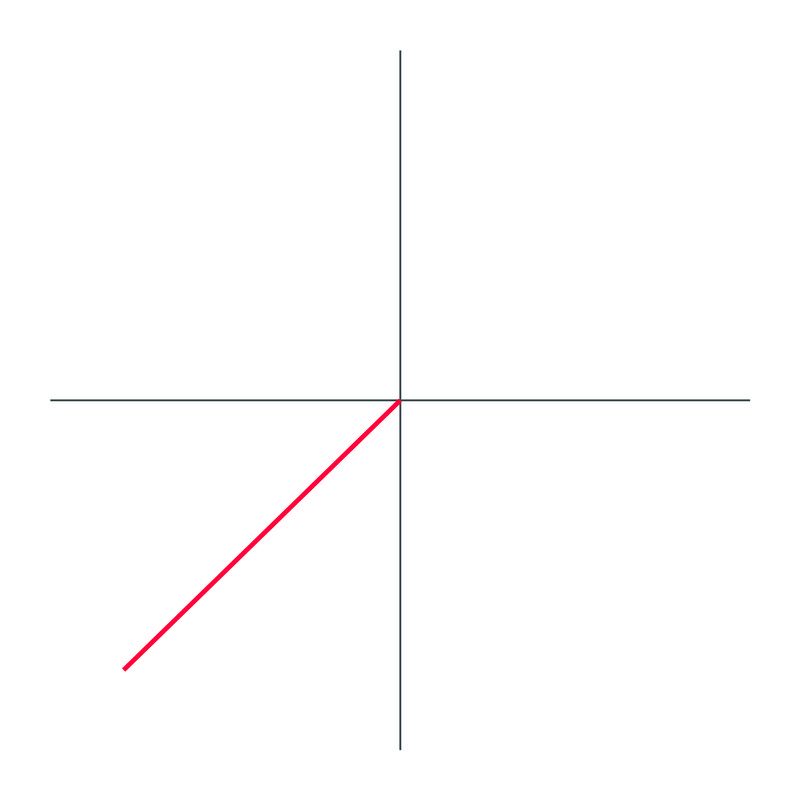
Solution
The angle drawn out is \(−135^{\circ}\).
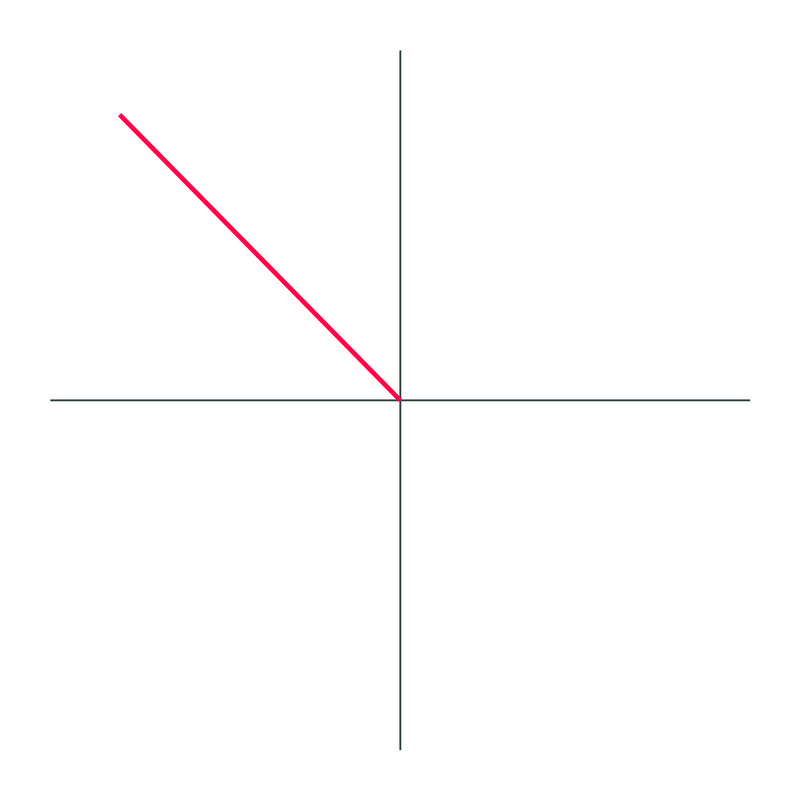
Identify what the angle is in this graph, using negative angles:
Solution
The angle drawn out is \(−180^{\circ}\).
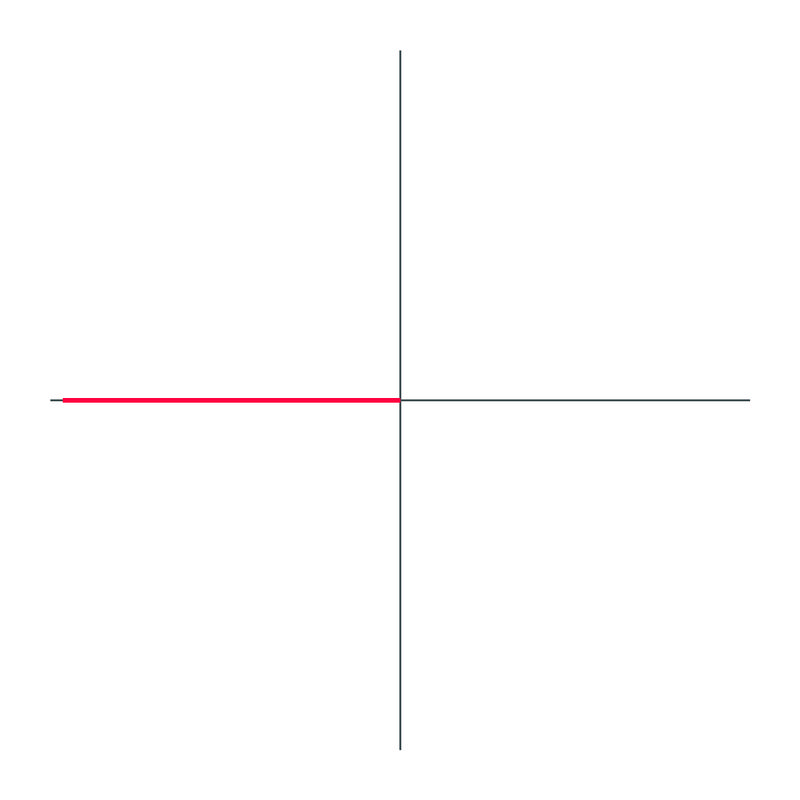
Identify what the angle is in this graph, using negative angles:
Solution
The angle drawn out is \(−225^{\circ}\).
Review
- Draw an angle of \(90^{\circ}\).
- Draw an angle of \(45^{\circ}\).
- Draw an angle of \(−135^{\circ}\).
- Draw an angle of \(−45^{\circ}\).
- Draw an angle of \(−270^{\circ}\).
- Draw an angle of \(315^{\circ}\).
For each diagram, identify the angle. Write the angle using positive degrees.
-
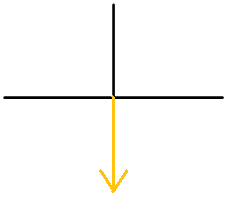
Figure \(\PageIndex{11}\) -
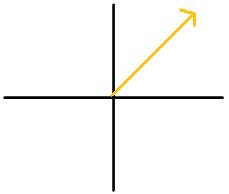
Figure \(\PageIndex{12}\) -
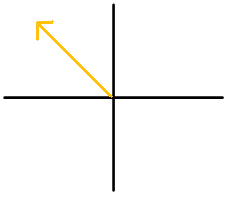
Figure \(\PageIndex{13}\)
For each diagram, identify the angle. Write the angle using negative degrees.
-
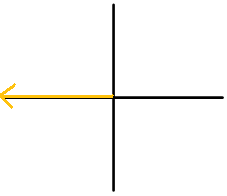
Figure \(\PageIndex{14}\) -
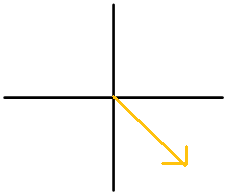
Figure \(\PageIndex{15}\) -
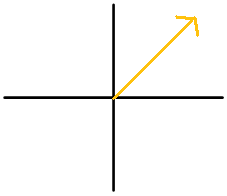
Figure \(\PageIndex{16}\) - Explain how to convert between angles that use positive degrees and angles that use negative degrees.
- At what angle is the 7 on a standard 12-hour clock? Use positive degrees.
- At what angle is the 2 on a standard 12-hour clock? Use positive degrees.
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.15.
Vocabulary
| Term | Definition |
|---|---|
| Quadrantal Angle | A quadrantal angle is an angle that has its terminal side on one of the four lines of axis: positive \(x\), negative \(x\), positive \(y\) or negative \(y\). |
| Standard Position | The standard position of an angle measures an angle starting from the positive \(x\)-axis and going counter-clockwise. It is the typical method for drawing and measuring an angle. |
Additional Resources
Video: Angles in Standard Position
Practice: Angles of Rotation in Standard Positions

