2.5.3: Trig Functions and Radians with Technology
- Page ID
- 4235
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Degrees versus radians and calculator modes.
Six Trigonometric Functions and Radians
While working in your math class one day, you are given a sheet of values in radians and asked to find the various trigonometric functions of them, such as sine, cosine, and \tan gent. The first question asks you to find the \(\sin \dfrac{\pi }{6}\). You are about to start converting the measurements in radians into degrees when you wonder if it might be possible to just take the values of the functions directly.
Do you think this is possible? As it turns out, it is indeed possible to apply trig functions to measurements in radians. Here you'll learn to do just that.
Trigonometric Functions and Radians
Even though you are used to performing the trig functions on degrees, they still will work on radians. The only difference is the way the problem looks. If you see \(\sin \dfrac{\pi }{6}\), that is still \(\sin 30^{\circ} \) and the answer is still \(\dfrac{1}{2}\).
Most scientific and graphing calculators have a MODE setting that will allow you to either convert between the two, or to find approximations for trig functions using either measure. It is impor\tan t that if you are using your calculator to estimate a trig function that you know which mode you are using. Look at the following screen:
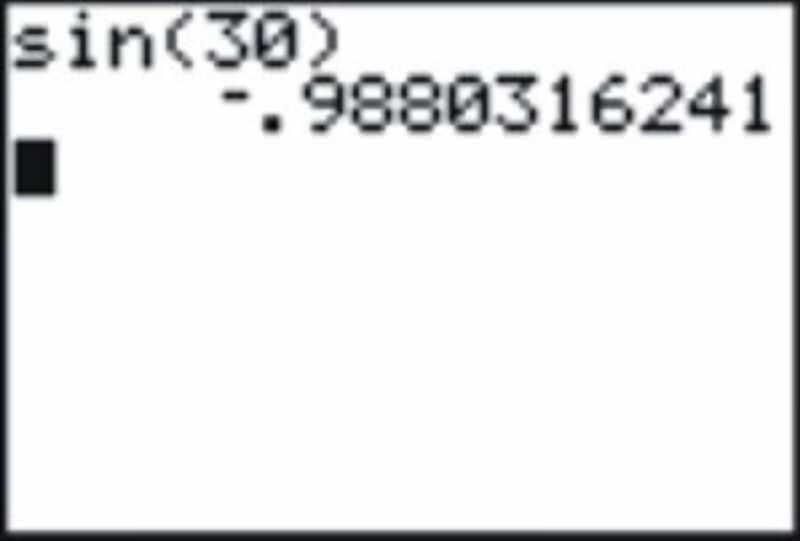
If you entered this expecting to find the sine of 30 degrees you would realize that something is wrong because the answer should be \(\dfrac{1}{2}\). In fact, as you may have suspected, the calculator is interpreting this as 30 radians. In this case, changing the mode to degrees and recalculating will give the expected result.

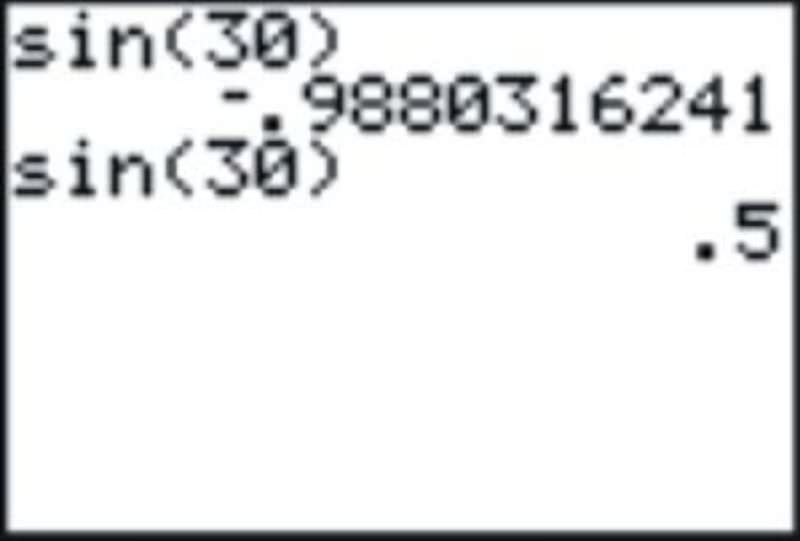
Scientific calculators will usually have a 3-letter display that shows either DEG or RAD to tell you which mode the calculator is in.
Let's take a look at a few example problems.
1. Find \(\tan \dfrac{3\pi }{4}\).
If needed, convert \(\dfrac{3\pi }{4}\) to degrees. Doing this, we find that it is 1\(35^{\circ} \). So, this is \(\tan 135^{\circ} \), which is -1.
2. Find the value of \(\cos \dfrac{11 \pi }{6}\).
If needed, convert \(\dfrac{11 \pi }{6}\) to degrees. Doing this, we find that it is \(330^{\circ} \). So, this is \(\cos 330^{\circ} \), which is \(\dfrac{\sqrt{3}}{2}\).
3. Convert 1 radian to degree measure.
Many students get so used to using \(\pi \) in radian measure that they incorrectly think that 1 radian means \(1\pi \) radians. While it is more convenient and common to express radian measure in terms of \(\pi \), don’t lose sight of the fact that \(\pi \) radians is a number. It specifies an angle created by a rotation of approximately 3.14 radius lengths. So 1 radian is a rotation created by an arc that is only a single radius in length.
\(\text{radians } \times \dfrac{180}{\pi }=\text{degrees}\)
So 1 radian would be \(\dfrac{180}{\pi }\) degrees. Using any scientific or graphing calculator will give a reasonable approximation for this degree measure, approximately \(57.3^{\circ} \).
Earlier, you were asked to find \(\sin \dfrac{\pi }{6}\).
Solution
As you have learned in this section, the \(\sin \dfrac{\pi }{6}\) is the same as \(\sin 30^{\circ} \), which equals \(\dfrac{1}{2}\). You could find this either by converting \(\dfrac{\pi }{6}\) to degrees, or by using your calculator with angles entered in radians.
Using a calculator, find the approximate degree measure (to the nearest tenth) of the angle expressed in radians:
Solution
\(\dfrac{6\pi }{7}\)
\(154.3^{\circ}\)
Using a calculator, find the approximate degree measure (to the nearest tenth) of the angle expressed in radians:
Solution
\(\dfrac{20\pi }{11}\)
\(327.3^{\circ}\)
Gina wanted to calculate the \(\sin 210^{\circ} \) and got the following answer on her calculator:
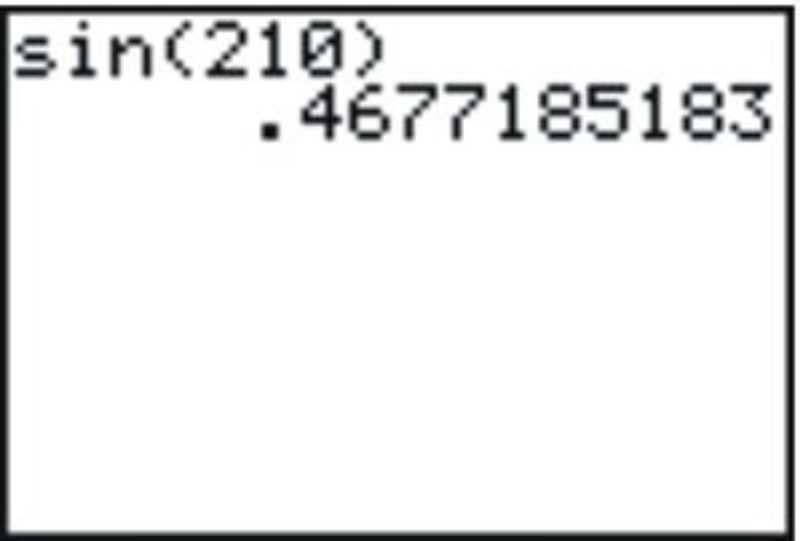
Solution
Fortunately, Kylie saw her answer and told her that it was obviously incorrect.
- Write the correct answer, in simplest radical form.
- Explain what she did wrong.
The correct answer is \(−\dfrac{1}{2}\). Her calculator was is the wrong mode and she calculated the sine of 210 radians.
Review
Using a calculator, find the approximate degree measure (to the nearest tenth) of the angle expressed in radians.
- \(\dfrac{4 \pi }{7}\)
- \(\dfrac{5 \pi }{6}\)
- \(\dfrac{8 \pi }{11}\)
- \(\dfrac{5 \pi }{3}\)
- \(\dfrac{8 \pi }{3}\)
- \(\dfrac{7 \pi }{4}\)
- \(\dfrac{12 \pi }{5}\)
Find the value of each using your calculator.
- \(\sin \dfrac{3\pi }{2}\)
- \(\cos \dfrac{\pi }{2}\)
- \(\tan \dfrac{\pi }{6}\)
- \(\sin \dfrac{5 \pi }{6}\)
- \(\tan \dfrac{4 \pi }{3}\)
- \(\cot \dfrac{7 \pi }{3}\)
- \(\sec \dfrac{11 \pi }{6}\)
- Do you think radians will always be written in terms of \pi ? Is it possible to have, for example, exactly 2 radians?
Review (Answers)
To see the Review answers, open this PDF file and look for section 2.3.
Vocabulary
| Term | Definition |
|---|---|
| radian | A radian is a unit of angle that is equal to the angle created at the center of a circle whose arc is equal in length to the radius. |
Additional Resources
Video: Examples: Determine Exact Trig Function Values With the Angle in Radians Using the Unit Circle

