2.5.4: Rotations in Radians

Rotation of clock hands.

In your math class one morning you finish a quiz early. While you are waiting, you watch the clock as it ticks off five minutes. The time on the clock reads 9:00. Your recent lessons have taught you that one way to measure the position of something on a circle is to use an angle. Suddenly it occurs to you that this can be applied to clocks. Can you determine the angle between the two hands of the clock?

A lot of interesting information about rotations and how to measure them can come from looking at clocks. We are so familiar with clocks in our daily lives that we don't often stop to think about these little devices, with hands continually rotating. Let's take a few minutes in this lesson for a closer look at these examples of rotational motion.

For the following problems, let's express in radians

1. The hands of a clock show 11:20. Express the obtuse angle formed by the hour and minute hands in radian measure.

The following diagram shows the location of the hands at the specified time.

Figure \(\PageIndex{1}\)

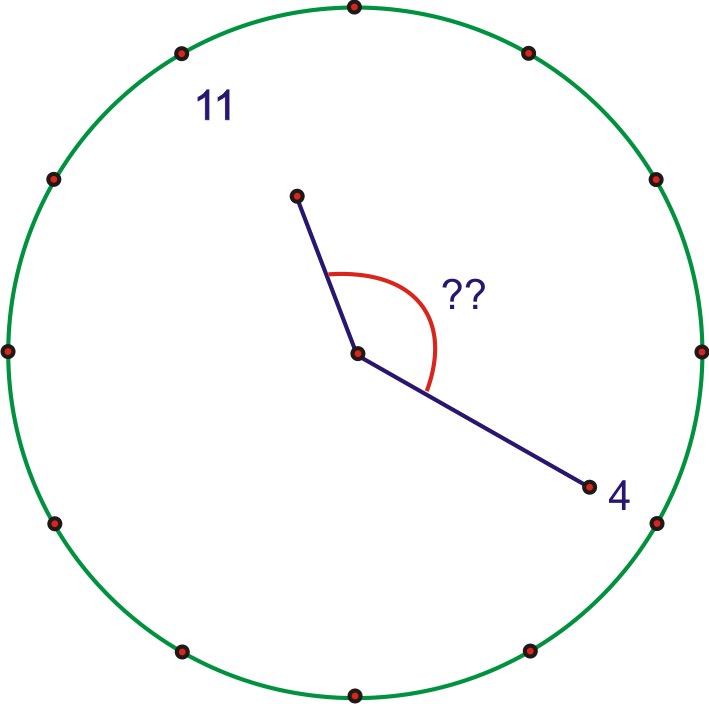
Because there are 12 increments on a clock, the angle between each hour marking on the clock is \(\dfrac{2\pi }{12}=\dfrac{\pi }{6}\) (or \(30^{\circ} \)). So, the angle between the 12 and the 4 is \(4\times \dfrac{\pi }{6}=\dfrac{2\pi }{3}\) (or \(120^{\circ}\) ). Because the rotation from 12 to 4 is one-third of a complete rotation, it seems reasonable to assume that the hour hand is moving continuously and has therefore moved one-third of the distance between the 11 and the 12. This means that the angle between the hour hand and the 12 is two-thirds of the distance between the 11 and the 12. So, \(\dfrac{2}{3}\times \dfrac{\pi }{6}=\dfrac{2\pi }{18}=\dfrac{\pi }{9}\), and the total measure of the angle is therefore \(\dfrac{\pi }{9}+\dfrac{2\pi }{3}=\dfrac{\pi }{9}+\dfrac{6\pi }{9}=\dfrac{7\pi }{9}\).

2. Express in radians

The hands of a clock show 4:15. Express the acute angle formed by the hour and minute hands in radian measure.

Figure \(\PageIndex{2}\)

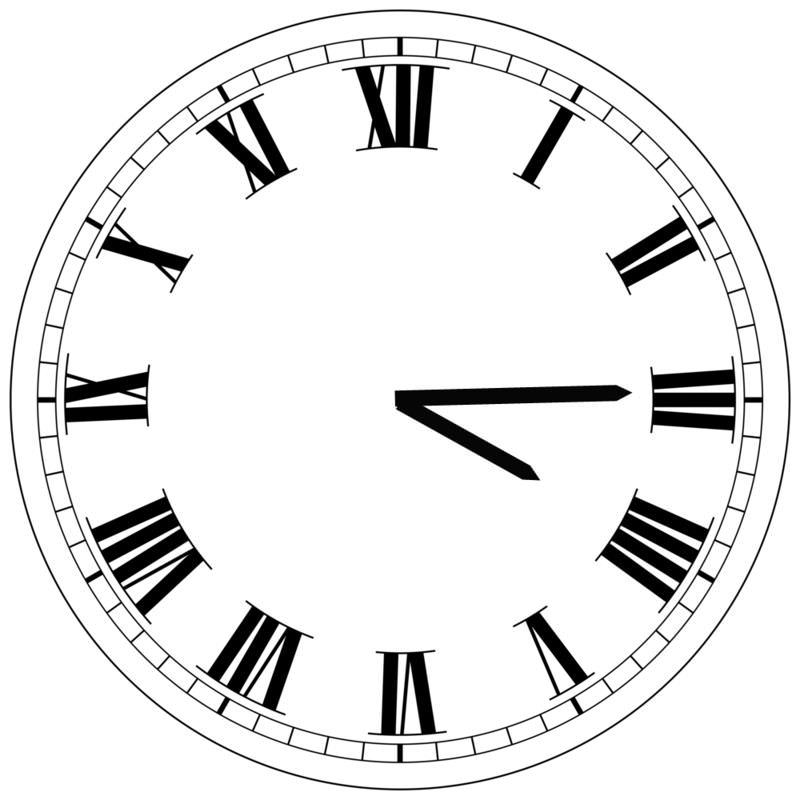
Because there are 12 increments on a clock, the angle between each hour marking on the clock is \(\dfrac{2\pi }{12}=\dfrac{\pi }{6}\) (or \(30^{\circ} \)). So, the angle between the 3 (which is where the minute hand is located when it is 15 minutes after the hour) and the 4 is \(\dfrac{\pi }{6}\) (or \(30^{\circ}\)). Further, since the minute hand has moved one quarter of the way around the hour, we can infer that the hour hand has moved one quarter of the way between four and five, which is \(\dfrac{1}{4}\times \dfrac{\pi }{6}=\dfrac{\pi }{24}\). Adding these numbers gives: \(\dfrac{\pi }{6}+\dfrac{\pi }{24}=\dfrac{4\pi }{24}+\dfrac{\pi }{24}=\dfrac{5\pi }{24}\).

3. The hands of a clock show 2:30. Express the acute angle formed by the hour and minute hands in radian measure.

Figure \(\PageIndex{3}\)

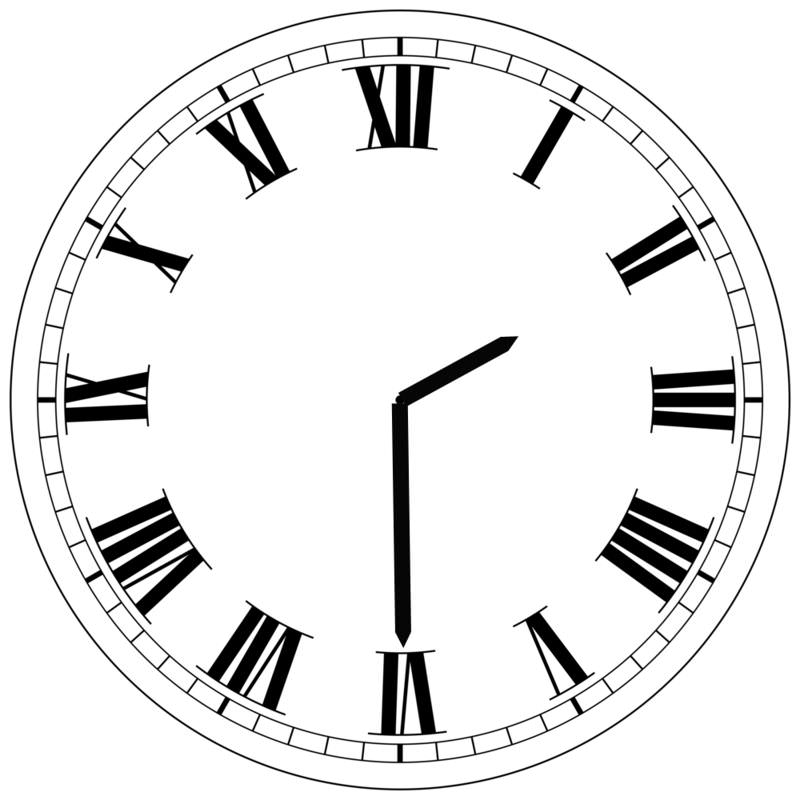
Because there are 12 increments on a clock, the angle between each hour marking on the clock is \(\dfrac{2\pi }{12}=\dfrac{\pi }{6}\) (or \(30^{\circ} \)). Since the hour hand would actually be partway between the 2 and the 3 at 2:30, start by determining the angular distance between the 3 and the 6, then you can add the additional portion between the 2 and the 3:

• The angle between the 3 and the 6 (which is where the minute hand is at 30 minutes after the hour) is \(3\times \dfrac{\pi }{6}=\dfrac{3\pi }{6}=\dfrac{\pi }{2}\) (or \(90^{\circ} \)).
• Because the rotation from 12 to 6 is one-half of a complete rotation, it seems reasonable to assume that the hour hand is moving continuously and has therefore moved one-half of the distance between the 2 and the 3. This means that the angle between the hour hand and the 3 is one-half of the distance between the 2 and the 3. So, \(\dfrac{1}{2}\times \dfrac{\pi }{6}=\dfrac{\pi }{12}\).
• The total measure of the angle is therefore \(\dfrac{\pi }{12}+\dfrac{\pi }{2}=\dfrac{\pi }{12}+\dfrac{6\pi }{12}=\dfrac{7\pi }{12}\).

Example \(\PageIndex{1}\)

Earlier, you were asked if you can determine the angle between the two hands of a clock.

Solution

Since you now know that the angle between the hours on a clock is \(\dfrac{\pi }{6}=30^{\circ} \), you can use this information to construct an answer. There are three hours between the 9 and the 12 on a clock, so the answer is:

\(3\times \dfrac{\pi }{6}=\dfrac{3\pi }{6}=\dfrac{\pi }{2}=90^{\circ}\)

So there are \(90^{\circ} \) degrees between the 9 and 12 on the clock.

The following image shows a 24-hour clock.

Figure \(\PageIndex{4}\)

Example \(\PageIndex{2}\)

What is the angle between each number of the clock expressed in exact radian measure in terms of \(\pi \)?

Solution

Since there are \(2\pi \) radians in a circle, and there are 24 separate increments, the answer is \(\dfrac{2\pi }{24}=\dfrac{\pi }{12}\)

Example \(\PageIndex{3}\)

What is the angle between each number of the clock expressed to the nearest tenth of a radian? What about in degree measure?

Solution

Since there are \(2\pi \) radians in a circle, the number of radians in each of 24 different divisions is \(\dfrac{2\pi }{24}\approx .3\). In degrees we can do the same by taking the number of degrees in a circle and dividing it by 12: \(\dfrac{360}{24}=15^{\circ} \).

Example \(\PageIndex{4}\)

Estimate the measure of the angle between the hands at the time shown to the nearest whole degree. And then in radian measure in terms of \(\pi \).

Solution

\(20^{\circ} \). Answers may vary, anything above \(15^{\circ} \) and less than \(25^{\circ} \) is reasonable. In radians, this is \(\dfrac{\pi }{9}\). Again, answers may vary.

Review

Use the clock below to help you find the angle between the hour hand and minute hand at each of the following times. Express your answer in degrees less than \(180^{\circ} \). Then express your answer in radian measure in terms of \(\pi \).

Figure \(\PageIndex{5}\)

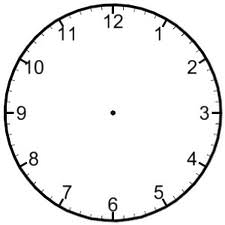
1. 3:30
2. 5:15
3. 4:45
4. 6:30
5. 6:15
6. 2:30
7. 12:30
8. 9:30
9. 10:15
10. 11:30
11. 3:45
12. 2:15
13. 7:15
14. How many times in 12 hours will the hour and minute hands overlap?
15. When is the first time after 12:00 that the hour and minute hands will overlap exactly?

Review (Answers)

To see the Review answers, open this PDF file and look for section 2.4.

Vocabulary

Term	Definition
radian	A radian is a unit of angle that is equal to the angle created at the center of a circle whose arc is equal in length to the radius.

Additional Resources

Interactive Element

Video: Examples: Determine Angles of Rotation

Practice: Rotations in Radians