2.5.5: Angular Velocity
- Page ID
- 4237
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Converting between linear and angular speeds using radius and circumference.
To find a particular song on your MP3/MP4 Player, you may use a scroll wheel. This involves moving your finger around the wheel in a circular motion. Unfortunately for you, the song you want is near the very bottom of your songs list. Since these media players can often hold over 1,000 songs, you have to scroll fast! As you are moving your finger in a circle, you might wonder if you could measure how fast your finger is covering the distance around the circle.
Watching your finger, you realize that your finger is moving around the circle twice every second. If the radius of the scroll wheel is 2 cm, what is the angular velocity of your finger as you scroll through your songs list? What is the linear velocity?
You may already be familiar with the measurement of speed as the relationship of an object's distance traveled to the time it has been in motion. However, this relationship is for objects that are moving in a straight line. What about objects that are traveling on a circular path?
Do you remember playing on a merry-go-round when you were younger?

If two people are riding on the outer edge, their velocities should be the same. But, what if one person is close to the center and the other person is on the edge? They are on the same object, but their speed is actually not the same.
Look at the following drawing.
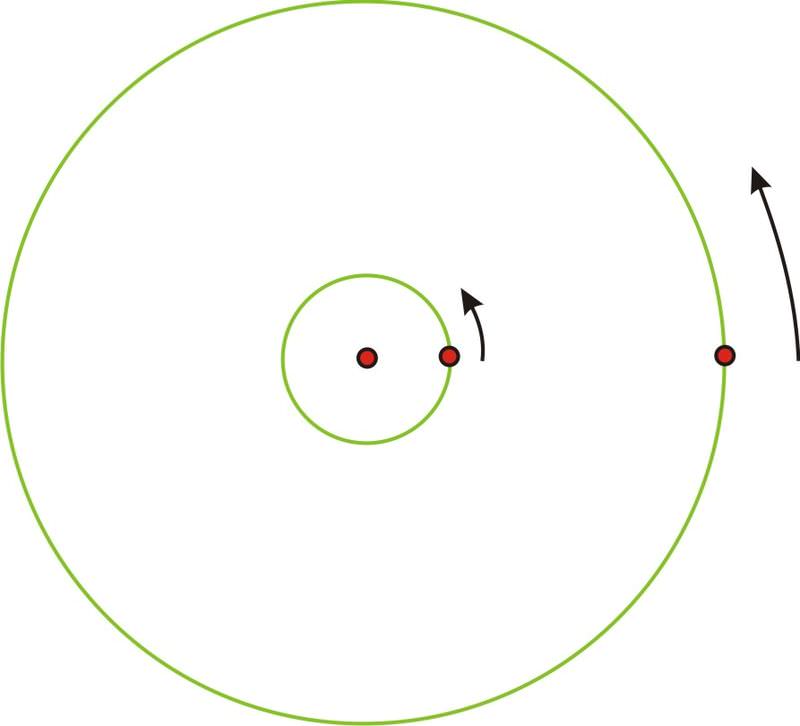
Imagine the point on the larger circle is the person on the edge of the merry-go-round and the point on the smaller circle is the person towards the middle. If the merry-go-round spins exactly once, then both individuals will also make one complete revolution in the same amount of time.
However, it is obvious that the person in the center did not travel nearly as far. The circumference (and of course the radius) of that circle is much smaller and therefore the person who traveled a greater distance in the same amount of time is actually traveling faster, even though they are on the same object. So the person on the edge has a greater linear velocity (recall that linear velocity is found using distance=rate ⋅ time). If you have ever actually ridden on a merry-go-round, you know this already because it is much more fun to be on the edge than in the center! But, there is something about the two individuals traveling around that is the same. They will both cover the same rotation in the same period of time. This type of speed, measuring the angle of rotation over a given amount of time is called the angular velocity.
The formula for angular velocity is:
\(\omega =\dfrac{\theta }{t}\)
\(\omega \) is the last letter in the Greek alphabet, omega, and is commonly used as the symbol for angular velocity. \theta is the angle of rotation expressed in radian measure, and t is the time to complete the rotation.
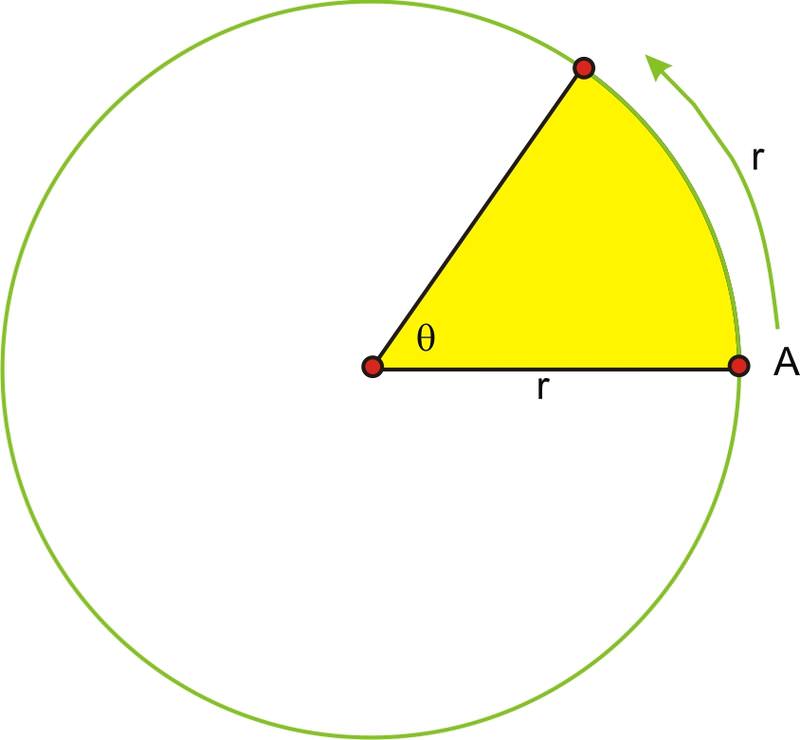
In this drawing, \(\theta \) is exactly one radian, or the length of the radius bent around the circle. If it took point A exactly 2 seconds to rotate through the angle, the angular velocity of A would be:
\(\begin{aligned} \omega &=\dfrac{\theta }{t}\\ \omega &=\dfrac{1}{2} \text{ radians per second} \end{aligned}\)
In order to know the linear speed of the particle, we would have to know the actual distance, that is, the length of the radius. Let’s say that the radius is 5 cm.
If linear velocity is v=dt then, \(v=\dfrac{5}{2}\) or \(2.5 \text{ cm per second}\).
If the angle were not exactly 1 radian, then the distance traveled by the point on the circle is the length of the arc, \(s=r\theta \), or, the radius length times the measure of the angle in radians.
Substituting into the formula for linear velocity gives: \(v=\dfrac{r\theta }{t}\) or \(v=r\cdot \dfrac{\theta }{t}\).
Look back at the formula for angular velocity. Substituting \(\omega \) gives the following relationship between linear and angular velocity, \(v=r\omega \). So, the linear velocity is equal to the radius times the angular velocity.
Remember in a unit circle, the radius is 1 unit, so in this case the linear velocity is the same as the angular velocity.
\(\begin{aligned} v &=r\omega \\ v&=1\times \omega \\ v&=\omega \end{aligned}\)
Here, the distance traveled around the circle is the same for a given unit of time as the angle of rotation, measured in radians.
Calculating the Linear and Angular Velocity
1. Lindsay and Megan are riding on a Merry-go-round. Megan is standing 2.5 feet from the center and Lindsay is riding on the outside edge 7 feet from the center. It takes them 6 seconds to complete a rotation. Calculate the linear and angular velocity of each girl.
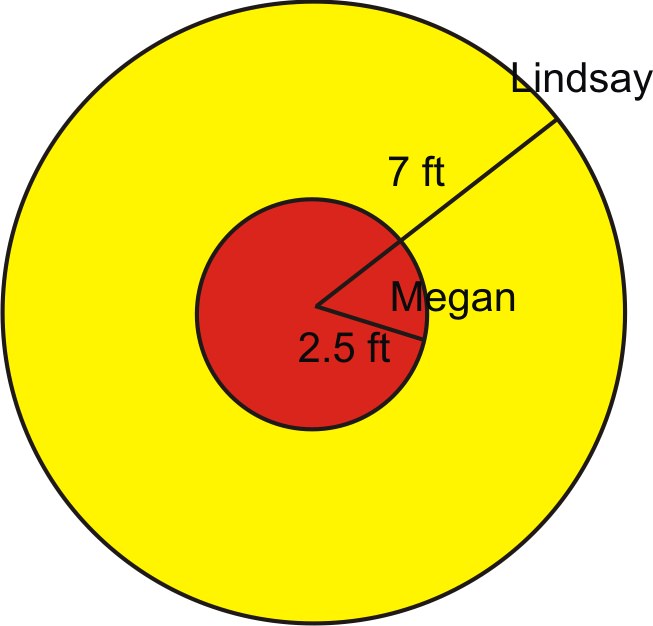
We are told that it takes 6 seconds to complete a rotation. A complete rotation is the same as \(2\pi \) radians. So the angular velocity is:
\(\omega =\dfrac{\theta }{t}=\dfrac{2\pi }{6}=\dfrac{\pi }{3}\) radians per second, which is slightly more than 1 (about 1.05), radian per second. Because both girls cover the same angle of rotation in the same amount of time, their angular speed is the same. In this case they rotate through approximately 60 degrees of the circle every second.
As we discussed previously, their linear velocities are different. Using the formula, Megan’s linear velocity is:
\(v=r\omega =(2.5)\left(\dfrac{\pi }{3}\right)\approx 2.6 \text{ ft per sec}\)
Lindsay’s linear velocity is:
\(v=r\omega =(7)\left(\dfrac{\pi }{3}\right)\approx 7.3 \text{ ft per sec}\)
2. A bug is standing near the outside edge of a compact disk (so that his radius from the center of the disc is 6 cm) that is rotating. He notices that he has traveled \(\pi \) radians in two seconds. What is his angular velocity? What is his linear velocity?

We know that the equation for angular velocity is
\(\omega =\dfrac{\theta }{t}=\dfrac{\pi }{2} \text{ radians per second}\).
We can use the given equation to find his linear velocity:
\(v=r\omega =(6)(\dfrac{\pi }{2})\approx 9.42 \text{ cm per sec}\)
Solving for Unknown Values
How long does it take the bug in the previous problem to go through two complete turns?
Since the angular velocity of the bug is \(\dfrac{\pi }{2}\) radians per second, we can use the equation for angular velocity and solve for time:
\(\begin{aligned} \omega &=\dfrac{\theta }{t} \\ t&=\theta \omega \end{aligned}\)
Since there are \(4\pi \) radians in two complete turns of the disc, we can use this for the value of \theta :
\(t=\dfrac{4\pi }{\dfrac{\pi }{2}}=4\pi \times \dfrac{2}{\pi} =8 \text{ seconds}\)
Earlier, you were asked to find the angular and linear velocity of your finger.
Solution
As you found out in this section, the angular velocity is the change in angle divided by the change in time. Since you sweep around the circle twice in a second, this becomes:
\(\omega =\dfrac{4\pi }{1}=4\pi \text{ rad/sec}\)
Further, you can find the linear velocity with the equation:
\(v=r\omega =(2)(4\pi )=8\pi \approx 25.132 \text{ cm/s}\)
Doris and Lois go for a ride on a carousel. Doris rides on one of the outside horses and Lois rides on one of the smaller horses near the center. Lois’ horse is 3 m from the center of the carousel, and Doris’ horse is 7 m farther away from the center than Lois’. When the carousel starts, it takes them 12 seconds to complete a rotation.
Calculate the linear velocity of each girl. Calculate the angular velocity of the horses on the carousel.
Solution
It is actually easier to calculate the angular velocity first. \(\omega =\dfrac{2\pi }{12}=\dfrac{\pi }{6}\), so the angular velocity is \(\dfrac{\pi }{6}\) rad, or \(0.524\). Because the linear velocity depends on the radius, each girl has her own.
Lois: \(v=r\omega =3\cdot \dfrac{\pi }{6}=\dfrac{\pi }{2}\) or \(1.57 \text{ m/sec}\)
Doris: \(v=r\omega =10\cdot \dfrac{\pi }{6}=\dfrac{5 \pi }{3}\) or \(5.24 \text{ m/sec}\)
The Large Hadron Collider near Geneva, Switzerland began operation in 2008 and is designed to perform experiments that physicists hope will provide important information about the underlying structure of the universe. The LHC is circular with a circumference of approximately 27,000 m. Protons will be accelerated to a speed that is very close to the speed of light (\(\approx 3\times 10^8\) meters per second).
How long does it take a proton to make a complete rotation around the collider? What is the approximate (to the nearest meter per second) angular speed of a proton traveling around the collider? Approximately how many times would a proton travel around the collider in one full second?
Solution
\(v=\dfrac{d}{t}\rightarrow 3\times 10^8=\dfrac{27,000}{t} \rightarrow t= \dfrac{2.7\times 10^4}{3\times 10^8}=0.9\times 10^{−4}=9\times 10^{−5} \text{ or } 0.00009 \text{ seconds}\)
\(\omega =\dfrac{\theta }{t}=\dfrac{2\pi }{0.00009}\approx 69,813 \text{ rad/sec}\)
The proton rotates around once in 0.00009 seconds. So, in one second it will rotate around the LHC \(1\div 0.00009=11,111.11\) times, or just over 11,111 rotations.
Ted is standing 2 meters from the center of a merry go round. If his linear velocity is 6 m/s, what is his angular velocity?
Solution
Since the equation relating linear and angular velocity is given by \(v=r\omega \), we can solve for omega: \(\omega =\dfrac{v}{r}=\dfrac{6}{2}=3\)
Review
Beth and Steve are on a carousel. Beth is 7 ft from the center and Steve is right on the edge, 7 ft further from the center than Beth. Use this information and the following picture to answer questions 1-6.
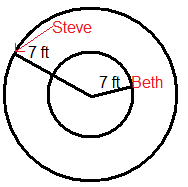
- The carousel makes a complete revolution in 12 seconds. How far did Beth go in one revolution? How far did Steve go in one revolution?
- If the carousel continues making revolutions every 12 seconds, what is the angular velocity of the carousel?
- What are Beth and Steve's linear velocities?
- How far away from the center would Beth have to be in order to have a linear velocity of \(\pi \) ft per second.
- The carousel changes to a new angular velocity of \(\dfrac{\pi }{3}\) radians per second. How long does it take to make a complete revolution now?
- With the carousel's new velocity, what are Beth and Steve's new linear velocities?
- Beth and Steve go on another carousel that has an angular velocity of \(\dfrac{\pi }{8}\) radians per second. Beth's linear velocity is \(2\pi\) feet per second. How far is she standing from the center of the carousel?
- Steve's linear velocity is only \(\dfrac{\pi }{3}\) feet per second. How far is he standing from the center of the carousel?
- What is the angular velocity of the minute hand on a clock? (in radians per minute)
- What is the angular velocity of the hour hand on a clock? (in radians per minute)
- A certain clock has a radius of 1 ft. What is the linear velocity of the tip of the minute hand?
- On the same clock, what is the linear velocity of the tip of the hour hand?
- The tip of the minute hand on another clock has a linear velocity of 2 inches per minute. What is the radius of the clock?
- What is the angular velocity of the second hand on a clock? (in radians per minute)
- The tip of the second hand on a clock has a linear velocity of 2 feet per minute. What is the radius of the clock?
Review (Answers)
To see the Review answers, open this PDF file and look for section 2.8.
Vocabulary
| Term | Definition |
|---|---|
| angular speed | Angular speed is the ratio of revolutions that occur per unit of time. |
| Angular Velocity | The angular velocity of a rotating object is the change in angle of an object divided by the change in time. |
| dimensional analysis | Dimensional analysis is a process for converting from one unit to another. |
| linear speed | Linear speed is the ratio of distance per unit of time. |
| Linear Velocity | The linear velocity of an object is the change in position of an object divided by the change in time. |
| radian | A radian is a unit of angle that is equal to the angle created at the center of a circle whose arc is equal in length to the radius. |
Additional Resources
Video: Linear Velocity and Angular Velocity
Practice: Angular Velocity
Real World: Building Momentum

