2.5.7: Area of a Sector
- Page ID
- 14922
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Half the radius squared times the angle in radians.
While eating lunch with your friends one day you decide to get some pie. The school cafeteria has a sale on pies if you buy the whole pie instead of an individual slice. Since you and your friends plan to eat the whole pie anyway, you are happy to make the purchase.
You decide to cut yourself a piece. When you have taken your section of pie out, one of your friends objects that you have cut out more than your fair share. If the radius of the pie is six inches, and the angle formed by the end of your pie wedge is \(30^{\circ}\), what is the area of your pie piece? Is it more than your fair share if there are five people (including you) splitting the pie?
Area of a Sector
One of the most common geometric formulas is the area of a circle:
\(A=\pi r^2\)
In terms of angle rotation, this is the area created by \(2\pi \) radians.
\(2\pi \text{ rad}=\pi r^2 \text{ area}\)
A half-circle, or \(\pi \) radian rotation would create a section, or sector of the circle equal to half the area or:
\(\dfrac{1}{2} \pi r^2\)
So an angle of 1 radian would define an area of a sector equal to:
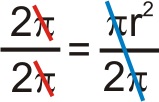
\(1=\dfrac{1}{2}r^2\)
From this we can determine the area of the sector created by any angle, \(\theta \) radians, to be:
\(A=\dfrac{1}{2}r^2\theta\)
Finding the Area
1. Crops are often grown using a technique called center pivot irrigation that results in circular shaped fields.

Here is a satellite image taken over fields in Kansas that use this type of irrigation system.

If the irrigation pipe is 450 m in length, what is the area that can be irrigated after a rotation of \(\dfrac{2\pi }{3}\) radians?
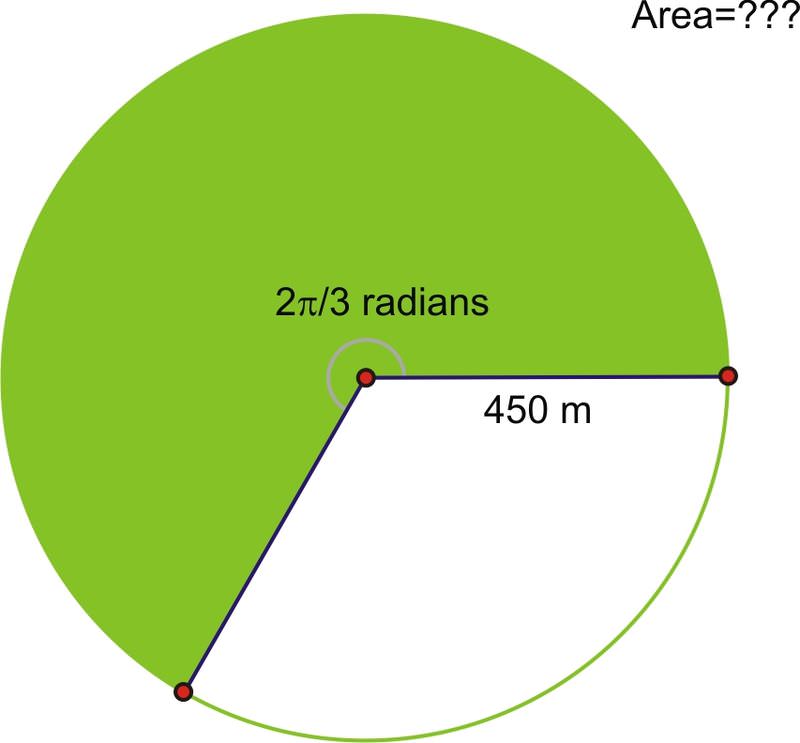
Using the formula:
\(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ A&=\dfrac{1}{2}(450)^2\left(\dfrac{2\pi }{3}\right)\end{aligned}\)

The area is approximately 212,058 square meters.
2. A doughnut has a hole in the middle with a radius of 1 cm, and the distance from the center of the hole to the outer edge of the doughnut is 3 cm. What is the area of a sector of 14 of the doughnut?

The formula for the area of a sector is \(A=\dfrac{1}{2}r^2\theta \). Using this formula to find the area of the sector from the center outward gives:
\(\begin{aligned} A &=\dfrac{1}{2}r^2 \theta \\ A &=\dfrac{1}{2}3^2 \dfrac{\pi }{2}\\ A&=\dfrac{9\pi }{4} \end{aligned}\)
Now it is necessary to subtract the area of the sector that is part of the hole, and therefore not part of the doughnut:
\(\begin{aligned} A &= \dfrac{1}{2}r^2 \theta \\ A &=\dfrac{1}{2} (1)^2 \dfrac{\pi }{2}\\ A&=\pi 4 \end{aligned}\)
Area of the sector of doughnut: \(A=\dfrac{9\pi }{4}−\dfrac{\pi }{4}=\dfrac{8\pi }{4}=2\pi\)
3. A driver is traveling around a circular track that has radius of 70 meters. If the angle from the starting line to her current position is \(\dfrac{\pi }{3}\) radians, what is the area of the sector traced out by her car?

The area of a sector is: \(A=\dfrac{1}{2}r^2\theta \). This leads us to:
\(\begin{aligned} A &=\dfrac{1}{2}r^2\theta \\ A &=\dfrac{1}{2}(70)^2 \dfrac{\pi }{3}\\ A&\approx 73.3 \text{ meters} \end{aligned}\)
Earlier, you were asked what is the area of your pie piece.
Solution
You now know that the equation for the area of a circle swept out by some angle is:
\(A=\dfrac{1}{2}r^2\theta\)
Applying this to your pie slice, you have an area of:
\(A=\dfrac{1}{2}\times 62\times \dfrac{\pi }{6}=3\pi \)
And the total area of the pie is:
\(\pi r^2=36\pi\)
To find out what your fair portion of the pie is, multiply the total area by your fraction:
\(\dfrac{1}{5} \times 36\pi =7.2\pi\)
And since the piece you took is only 3\pi in size, you are definitely not taking too much!
If the radius of a sector is 5 feet, and the sector sweeps out an angle of \(43^{\circ}\), find the area of the sector.
Solution
Since you know that \(A=\dfrac{1}{2}r^2\theta \), you can solve for the area (don't forget to convert the degrees of the angle to radians):
\(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ A&=\dfrac{1}{2} (25)(.75) \\ A&=9.375 \end{aligned}\)
If a pie wedge has an area of 15 square in inches, and the pie has a radius of 9 inches, find the angle swept out by the sector.
Solution
Since you know that \(A=\dfrac{1}{2}r^2\theta \), you can solve for the angle swept out by the sector (don't forget that the angle will be measured in radians):
\(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ 15&=\dfrac{1}{2} (81)(\theta ) \\ \theta &=\dfrac{(2)(15)}{81} \\ \theta &=.37 \end{aligned}\)
If you have a piece of round cake that has an area of 20 square inches, and you know the piece sweeps out an angle of \(25^{\circ}\), find the radius of the cake.
Solution
Since you know that \(A=\dfrac{1}{2}r^2\theta \), you can solve for the radius of the cake (don't forget to convert the degrees of the angle to radians):
\(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ 20&=\dfrac{1}{2}(r^2)(.436) \\ r^2&=\dfrac{(2)(20)}{.436 }\\ r^2&=91.743 \\ r&=9.58 \end{aligned}\)
Review
- If the radius of a sector is 8 inches, and the central angle of the sector is \(40^{\circ}\), find the area of the sector.
- If the radius of a sector is 12 inches, and the central angle of the sector is \(\dfrac{\pi }{6}\) radians, find the area of the sector.
- If the radius of a sector is 6 inches, and the central angle of the sector is \(140^{\circ}\), find the area of the sector.
- If the radius of a sector is 5 inches, and the central angle of the sector is \(\dfrac{5\pi }{3}\) radians, find the area of the sector.
- If the radius of a sector is 10 inches, and the central angle of the sector is \(100^{\circ}\), find the area of the sector.
- If a pie wedge has an area of 10 square inches, and the pie has a radius of 6 inches, find the angle swept out by the sector.
- If a pie wedge has an area of 15 square inches, and the pie has a radius of 4 inches, find the angle swept out by the sector.
- If a pie wedge has an area of 12 square inches, and the pie has a radius of 3 inches, find the angle swept out by the sector.
- If you have a piece of round cake that has an area of 20 square inches, and you know the piece sweeps out an angle of \(\dfrac{\pi }{3}\) radians, find the radius of the cake.
- If you have a piece of round cake that has an area of 100 square inches, and you know the piece sweeps out an angle of \(50^{\circ}\), find the radius of the cake.
- If you have a piece of round cake that has an area of 35 square inches, and you know the piece sweeps out an angle of \(\dfrac{2\pi }{5}\) radians, find the radius of the cake.
- If you have a piece of round cake that has an area of 20 square inches, and you know the piece sweeps out an angle of \(30^{\circ}\), find the radius of the cake.
A pizza has a radius of 10 in. Use this information to answer questions 13-15.
- A slice is removed. The length of the crust of the missing slice is 3 in. What is the area of the missing slice?
- You eat three pieces with a central angle of \(\dfrac{4\pi }{5}\). What is the area of the pizza you ate?
- A large pizza has a radius of 12 in. What is the area of half of the large pizza?
Review (Answers)
To see the Review answers, open this PDF file and look for section 2.6.
Vocabulary
| Term | Definition |
|---|---|
| Sector | A sector of a circle is a portion of a circle contained between two radii of the circle. Sectors can be measured in degrees. |

