2.5.8: Length of a Chord
- Page ID
- 14923
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Twice the radius times the sine of half the angle in radians.
You have been asked to help the younger students at your school with their Physical Education class. While working one afternoon, you are asked to take out a parachute that the students can play with. As the students are playing, one of them walks across a small portion of the parachute instead of under it like she is supposed to. If the chute is shaped like a circle with a radius of 6 meters, and the path the student walked across the chute covered an angle of \(50^{\circ}\), what is the length of the path she walked across the parachute?
You may recall from your Geometry studies that a chord is a segment that begins and ends on a circle.
\(\overline{AB}\) is a chord in the circle.
We can calculate the length of any chord if we know the angle measure and the length of the radius. Because each endpoint of the chord is on the circle, the distance from the center to A and B is the same as the radius length.
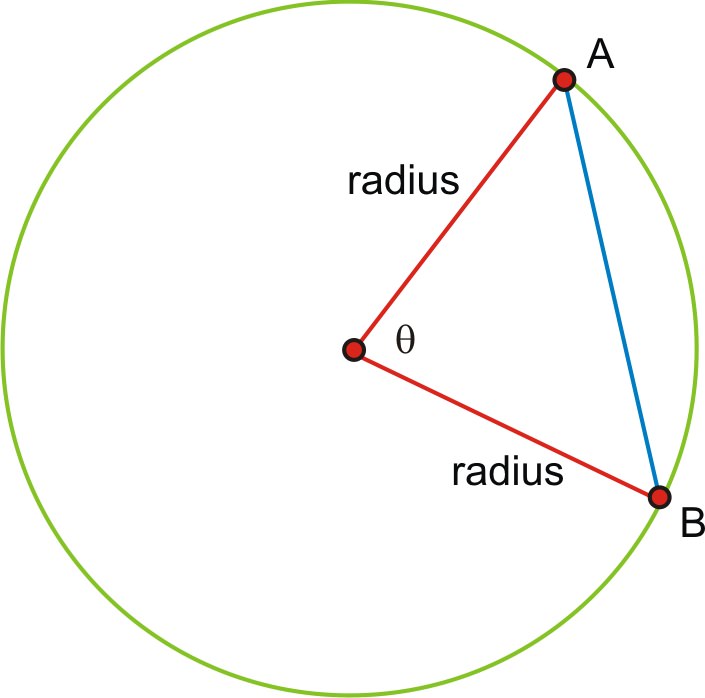
Next, if we bisect the angle, the angle bisector must be perpendicular to the chord and bisect it (we will leave the proof of this to your Geometry class). This forms a right triangle.
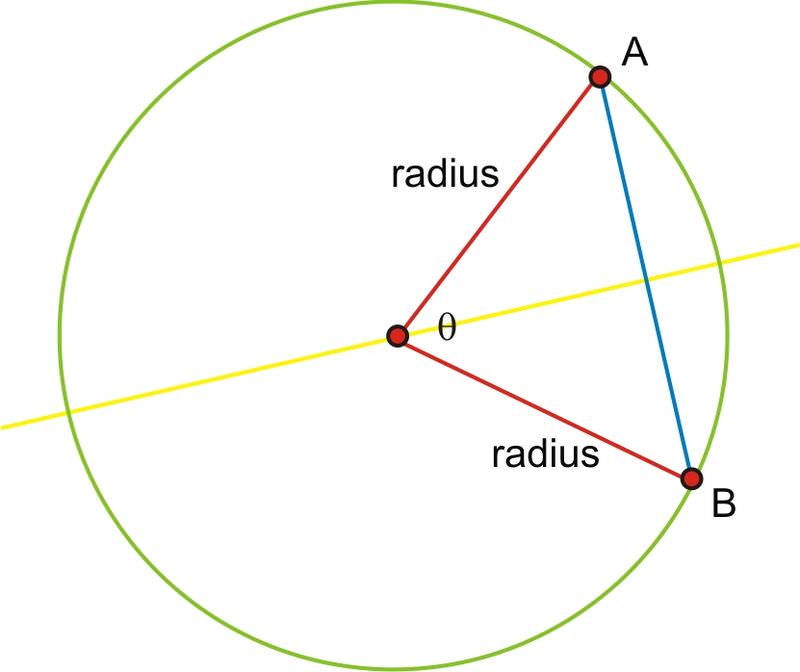
We can now use a simple sine ratio to find half the chord, called c here, and double the result to find the length of the chord.
\(\begin{aligned} \sin\dfrac{\theta}{2}&=\dfrac{c}{r} \\ c&=r\times \sin\dfrac{\theta}{2}\end{aligned}\)
So the length of the chord is:
\(2c=2r \sin\dfrac{\theta}{2}\)
Finding the Length of a Chord
1. Find the length of the chord of a circle with radius 8 cm and a central angle of \(110^{\circ}\). Approximate your answer to the nearest mm.
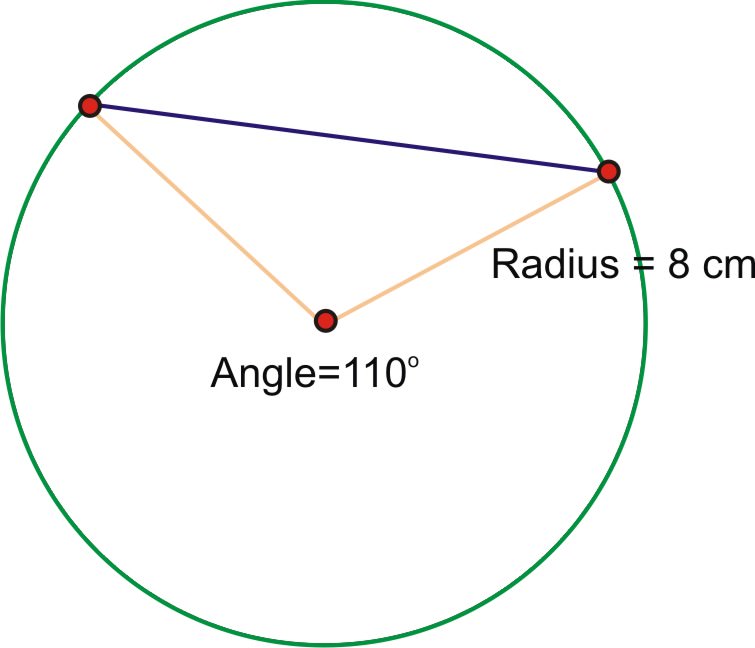
We must first convert the angle measure to radians:
\(110\times \dfrac{\pi }{180}=\dfrac{11\pi }{18}\)
Using the formula, half of the chord length should be the radius of the circle times the sine of half the angle.
\(\begin{aligned} \dfrac{11\pi }{18}\times \dfrac{1}{2}=\dfrac{11\pi }{36} \\ 8\times \sin \dfrac{11\pi }{36} \end{aligned}\)
Multiply this result by 2.
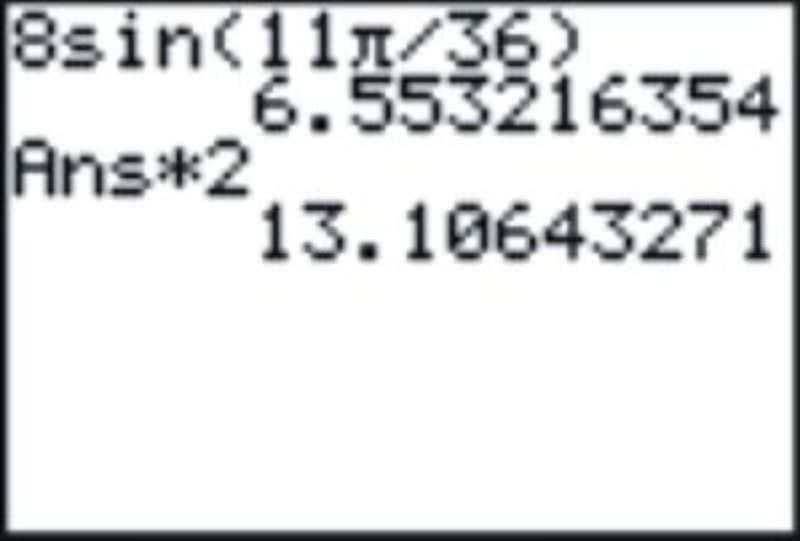
So, the length of the chord is approximately 13.1 cm.
2. Find the length of the chord of a circle with a radius of 2 m that has a central angle of \(90^{\circ}\).
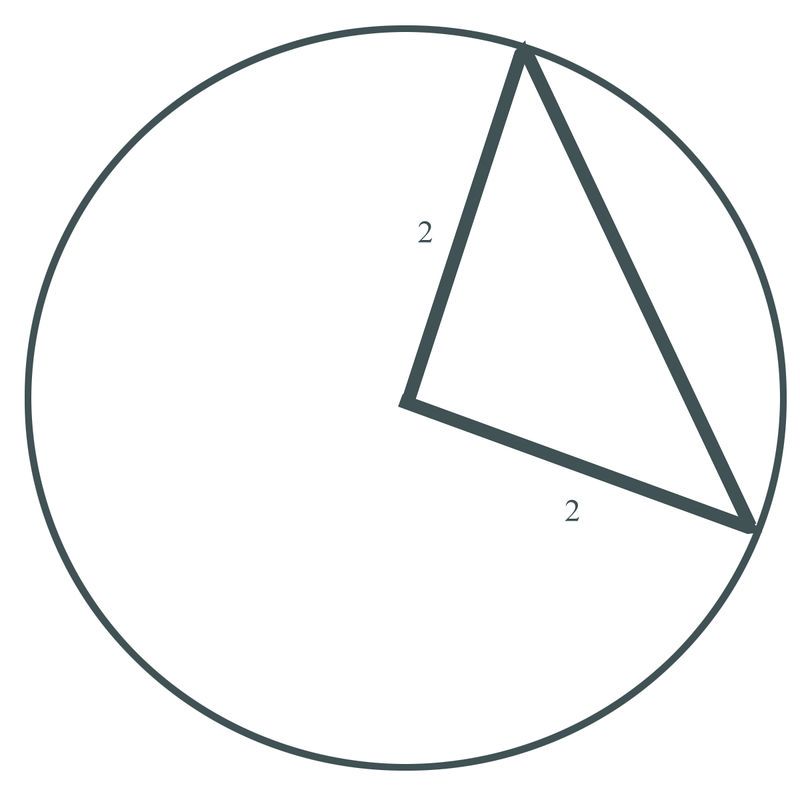
First convert the angle to radians:
\(90\times \dfrac{\pi }{180}=\dfrac{\pi }{2}\)
Using the formula, half of the chord length should be the radius of the circle times the sine of half the angle.
\(\dfrac{\pi }{2}\times \dfrac{1}{2}=\dfrac{\pi }{4} \\ 2\times \sin \dfrac{\pi }{4}\)
Multiply this result by 2.
So the answer is approximately 2.83 meters.
3. Find the length of the chord of a circle with radius 1 m and a central angle of \(170^{\circ}\).
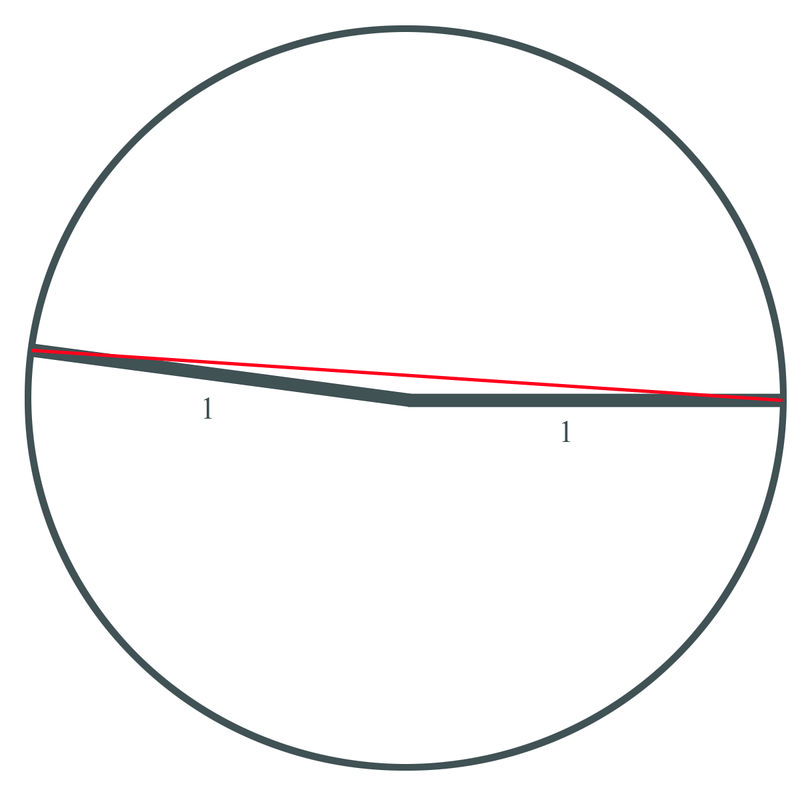
We must first convert the angle measure to radians:
\(170\times \dfrac{\pi }{180}=\dfrac{17\pi }{18}\)
Using the formula, half of the chord length should be the radius of the circle times the sine of half the angle.
\(\begin{aligned} \dfrac{17\pi }{18} \times \dfrac{1}{2}&= \dfrac{17\pi }{36} \\1\times \sin \dfrac{17\pi }{36}&=.996\end{aligned}\)
Multiply this result by 2.
So, the length of the arc is approximately 1.992
Notice that the length of the chord is almost 2 meters, which would be the diameter of the circle. If the angle had been 180 degrees, the chord would have just been the distance all the way across the circle going through the middle, which is the diameter.
Earlier, you were asked what is the length of the path she walked across the parachute.
Solution
With the equation for the length of a chord in hand, you can calculate the distance the student ran across the parachute:
First convert the measure in degrees to radians:
\(50\times \dfrac{\pi }{180} \approx .27\pi\)
\(2r \sin \dfrac{\theta}{2}=(2)(6)\sin \dfrac{.27\pi }{2}=12 \sin.135\pi \approx 4.94 \text{ meters}\)
If you run a piece of string across a doughnut you are eating, and the radius between the endpoints of the string to the center of the doughnut is 4 inches, how long is the string if the angle swept out by the chord is \(20^{\circ}\)?
Solution
You can use the equation \(C=2r\sin\left(\dfrac{\theta}{2}\right)\) to solve this problem: (Don't forget to convert angles to radians)
\(\begin{aligned} C&=2r\sin \left(\dfrac{\theta}{2}\right) \\ C&=(2)(4)\sin\left(\dfrac{.349}{2}\right) \\ C&=8(.1736) \\ C&=1.388 \text{ inches}\end{aligned}\)
You are eating dinner one night with your family at the local Italian restaurant. A piece of spaghetti makes a chord across your plate. You know that the length of the spaghetti strand is 5 inches, and the radius of the plate is 7 inches. What is the angle swept out by the chord?
Solution
Since the radius of the plate and the length of the chord are known, you can solve for the angle:
\(\begin{aligned}
C&=2 r \sin \left(\dfrac{\theta}{2}\right) \\
\dfrac{C}{2 r}&=\sin \left(\dfrac{\theta}{2}\right) \\
\sin ^{-1}\left(\dfrac{c}{2 r}\right)&=\dfrac{\theta}{2} \\
\sin ^{-1}\left(\dfrac{5}{14}\right)&=\dfrac{\theta}{2} \\
.365&=\dfrac{\theta}{2} \\
\theta&=.73
\end{aligned}\)
The angle spanned by the spaghetti is .73 radians.
If you draw a chord across a circle and make a chord across it that has a length of 15 inches, sweeping out an angle of \(\pi \) radians, what is the radius of the circle you drew?
Solution
Using the equation for the length of a chord:
\(\begin{aligned} c&=2r \sin(\dfrac{\theta }{2}) \\ 15&=(2r)\sin(\dfrac{\pi }{2}) \\ r&=7.5 \end{aligned}\)
As you can see, the radius of the circle is 7.5 inches. This is what you should expect, since the chord sweeps out an angle of \(\pi \). This means that it sweeps out half of the circle, so that the chord is actually going across the whole diameter of the circle. So if the chord is going across the diameter and has a length of 15 inches, then the radius of the circle should be 7.5 inches.
Review
- Find the length of the chord of a circle with radius 1 m and a central angle of \(100^{\circ}\).
- Find the length of the chord of a circle with radius 8 km and a central angle of \(130^{\circ}\).
- Find the length of the chord of a circle with radius 4 in and a central angle of \(45^{\circ}\).
- Find the length of the chord of a circle with radius 3 ft and a central angle of \(32^{\circ}\).
- Find the length of the chord of a circle with radius 2 cm and a central angle of \(112^{\circ}\).
- Find the length of the chord of a circle with radius 7 in and a central angle of \(135^{\circ}\).
Solve for the missing variable in each circle.
-
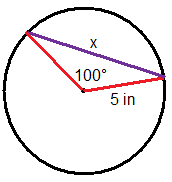
Figure \(\PageIndex{8}\) -
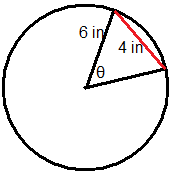
Figure \(\PageIndex{9}\) -
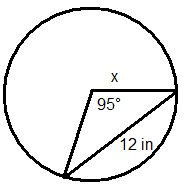
Figure \(\PageIndex{10}\) -
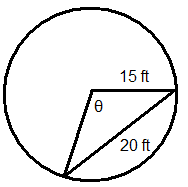
Figure \(\PageIndex{11}\) -
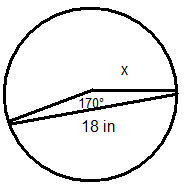
Figure \(\PageIndex{12}\) -
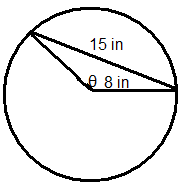
Figure \(\PageIndex{13}\)
Use the picture below for questions 13-15.
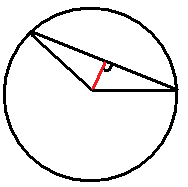
- Suppose you knew the length of the chord, the length of the radius, and the central angle of the above circle. Describe one way to find the length of the red segment using the Pythagorean Theorem.
- Suppose you knew the length of the chord, the length of the radius, and the central angle of the above circle. Describe one way to find the length of the red segment using cosine.
- What would you need to know in order to find the area of the segment (the portion of the circle between the chord and the edge of the circle)? Describe how to find the area of this region.
Review (Answers)
To see the Review answers, open this PDF file and look for section 2.7.
Vocabulary
| Term | Definition |
|---|---|
| Chord | A chord is a straight line across a circle, intersecting the circle in two places, but not passing through the circle's center. |

