2.5.6: Length of an Arc
- Page ID
- 4239
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Radius times the angle in radians.
You have taken your little cousin to the amusement park for the day. While there, she decides she would like a ride on the carousel. After the ride, she excitedly bounces over to you. She is amazed that she went around, but in a way ‘‘didn't go anywhere’’, since she ended up where she started.
‘‘How far did I go when I was halfway around the turn?’’, she asks.
You know that the radius of the carousel is 7 meters. Can you tell your little cousin how far she went in one half of a turn around the ride?
The length of an arc on a circle depends on both the angle of rotation and the radius length of the circle. If you recall from the last lesson, the measure of an angle in radians is defined as the length of the arc cut off by one radius length. What if the radius is 4 cm? Then, the length of the half-circle arc would be \(\pi \) multiplied by the radius length, or \(4\pi \) cm in length.
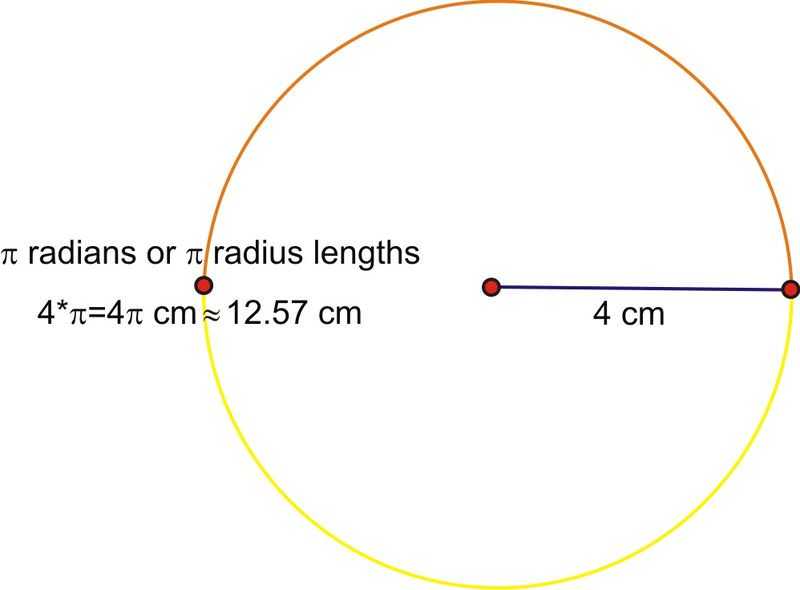
This results in a formula that can be used to calculate the length of any arc.
\(s=r\theta \),
where s is the length of the arc, r is the radius, and \theta is the measure of the angle in radians.
Solving this equation for \(\theta \) will give us a formula for finding the radian measure given the arc length and the radius length.
Let's look at some problems involving arc length.
1. Find the length of the arcs
The free-throw line on an NCAA basketball court is 12 ft wide. In international competition, it is only about 11.81 ft. How much longer is the half circle above the free-throw line on the NCAA court?
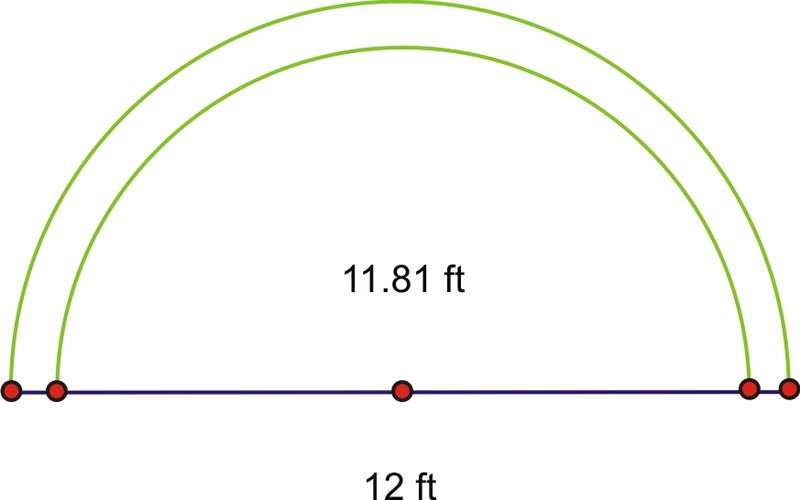
Find both arc lengths.
\(\begin{array}{l}
\text { NCAA } & \text { INTERNATIONAL }\\
s_{1}=r \theta & s_{2}=r \theta\\
s_{1}=\dfrac{12}{2}(\pi) & s_{2} \approx \dfrac{11.81}{2}(\pi)\\
s_{1}=6 \pi & s_{2} \approx 5.905 \pi
\end{array}\)
So the answer is approximately \(6\pi −5.905\pi \approx 0.095\pi\)
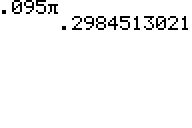
This is approximately 0.3 ft, or about 3.6 inches longer.
2. Two connected gears are rotating. The smaller gear has a radius of 4 inches and the larger gear’s radius is 7 inches. What is the angle through which the larger gear has rotated when the smaller gear has made one complete rotation?
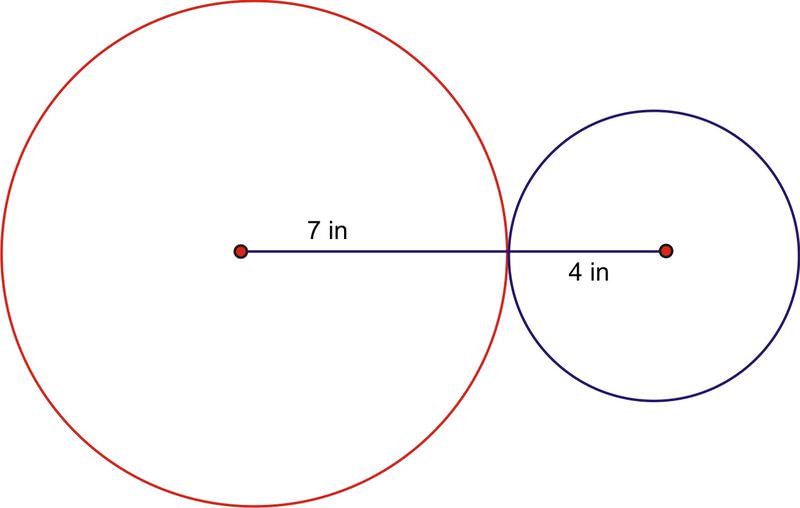
Because the blue gear performs one complete rotation, the length of the arc traveled is:
\(\begin{aligned} s &=r\theta \\ s&=4\times 2\pi \end{aligned}\)
So, an \(8\pi \) arc length on the larger circle would form an angle as follows:
\(\begin{aligned} \theta &=\dfrac{s}{r} \\ \theta &=\dfrac{8\pi }{7} \\ \theta &\approx 3.6 \end{aligned}\)
So the angle is approximately 3.6 radians.
\(3.6\times 180\pi \approx 206^{\circ}\)
3. The radius of a standard car tire is 27.94 cm. How far does a car go in one revolution of the tire?
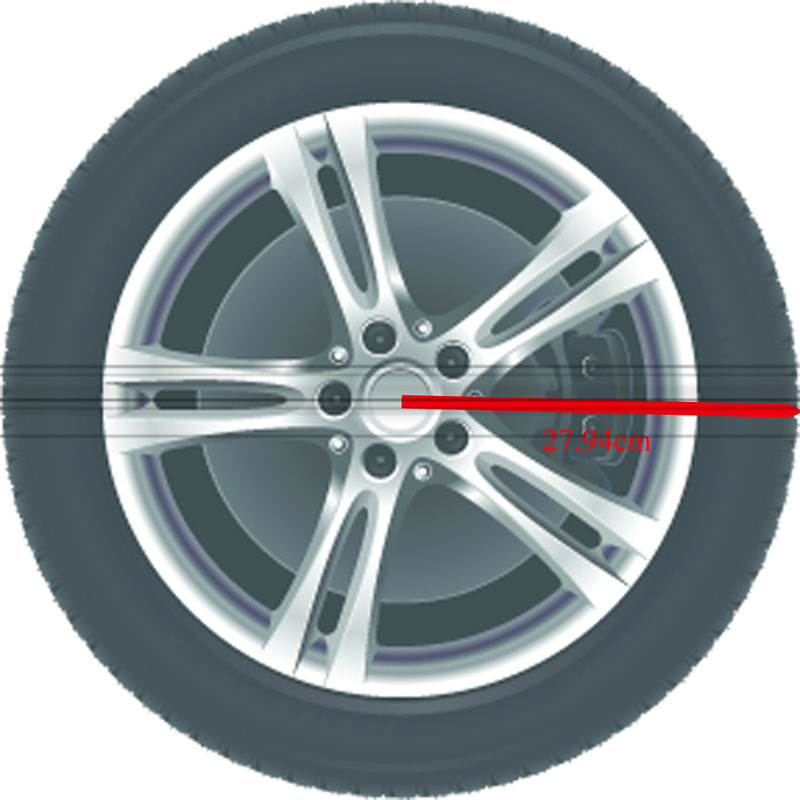
Since the distance traveled by the tire is equal to the distance around the tire, we can use the circumference of the tire to answer the question.
\(\begin{aligned} s &=r\theta \\ s&=(27.94)(2\pi )\\s=175.46 \end{aligned}\)
Earlier, you were asked can you tell your little cousin how far she went in one half of a turn around the ride.
Solution
Since you now know that you can measure an arc length using \(s=r\theta \), you can use this to find a solution to your cousin's question. Since your cousin wants to know how far she went around when she went \(\dfrac{1}{2}\) of a rotation, and the radius of the ride is 7 meters, you can calculate her arc length:
\(s=r\theta =7\pi \approx 21.98 \text{ meters}\)
You are trying to push your car after it has broken down. Unfortunately, you aren't very strong, and so the car is just rocking back and forth instead of rolling as you push. If the radius of your car's tire is 14 inches, and the change in the tire's angle is \(\dfrac{\pi}{2}\) radians, how far did the tire move?
Solution
Since the distance the tire moved is equal to the length of the arc the tire rolled, you can use the equation s=r\theta to determine how far the tire went:
\(\begin{aligned} s&=r\theta \\ s&=(14)\left(\dfrac{\pi}{2}\right) \\ s&=7\pi \\ s&\approx 21.98 \text{ in}\end{aligned}\)
If an object with a radius of 10 cm spins so that its arc covers 54 cm, what is the change in angle of the object?
Solution
You can again use the equation \(s=r\theta \) to solve this problem:
\(\begin{aligned} s&=r\theta \\ \theta &=\dfrac{s}{r}=\dfrac{54}{10}=5.4 \end{aligned}\)
The disk moves 5.4 radians, which is a little less than a complete rotation, since a complete rotation is approximately 6.28 radians.
If your DVD has a radius of 4.5 inches, how far does a point on the disk spin if the player turns it \dfrac{\pi}{2} radians?
Solution
Using \(s=r\theta \),
\(\begin{aligned} s&=r\theta \\ s&=(4.5)\left(\dfrac{\pi }{2}\right) \\ s&=2.25\pi \approx 7.065\end{aligned}\)
A point on the disk turns 7.065 inches.
Review
The radius of a carousel is 8 meters. Use this information to answer questions 1-3.
- You are half way around the carousel. How far did you travel?
- You are all the way around the carousel. How far did you travel?
- You have now traveled all the way around the carousel twice. How far did you travel?
A pizza has a radius of 10 in. Use this information to answer questions 4-6.
- A slice is removed. The length of the crust of the missing slice is 3 in. What is the central angle of the missing slice?
- You eat three pieces with a central angle of \(\dfrac{4\pi }{5}\). What is the length of the crust you ate?
- A large pizza has a radius of 12 in. What is the length of the crust of half of the large pizza?
The diameter of a tire is 35 in. Use this information to answer questions 7-10.
- What is the length around the whole tire?
- The tire travels one mile (5280 ft). How many revolutions did the tire make?
- You roll the tire so it rotates \(7\pi \) radians. How far did it move?
- The tire travels half a mile. How many radians did the tire rotate?
Consider a standard 12 hour clock like the one below with a radius of 5 inches. Use this to answer questions 11-15.
- What is the length of the arc between the 3 and the 7?
- What is the length of the arc between the 3 and the 2?
- It is 12:30. What is the length of the arc between the minute and hour hands?
- It is 7:20. What is the length of the arc between the minute and hour hands?
- It is 1:25. What is the length of the arc between the minute and hour hands?
Review (Answers)
To see the Review, open this PDF file and look for section 2.5.
Vocabulary
| Term | Definition |
|---|---|
| Arc | An arc is a section of the circumference of a circle. |
Additional Resources
Video: Arc Length, Area of Sector, Linear Speed, and Angular Speed - Example 5
Practice: Length of an Arc

