2.7.1: Graphing Tangent, Cotangent, Secant and Cosecant
- Page ID
- 14937
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Tangent, cotangent, cosecant, and secant graphs. Concept Map
If you already know the relationship between the equation and graph of sine and cosine functions then the other four functions can be found by identifying zeroes, asymptotes and key points. Are the four new functions transformations of the sine and cosine functions?
Graphing Other Trigonometric Functions
Secant and Cosecant
Since secant is the inverse of cosine the graphs are very closely related.
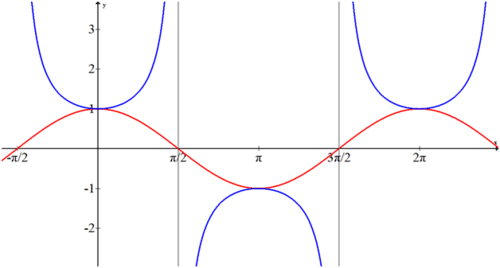
Notice wherever cosine is zero, secant has a vertical asymptote and where \(\cos x=1\) then \(\sec x=1\) as well. These two logical pieces allow you to graph any secant function of the form:
\(f(x)=\pm a\cdot \sec (b(x+c))+d\)
The method is to graph it as you would a cosine and then insert asymptotes and the secant curves so they touch the cosine curve at its maximum and minimum values. This technique is identical to graphing cosecant graphs. Simply use the sine graph to find the location and asymptotes.
Tangent and Cotangent
The tangent and cotangent graphs are more difficult because they are a ratio of the sine and cosine functions.
- \(\tan x=\dfrac{\sin x}{\cos x}\)
- \(\cot x=\dfrac{\cos x}{\sin x}\)
The way to think through the graph of \(f(x)=\tan x\) is to first determine its asymptotes. The asymptotes occur when the denominator, cosine, is zero. This happens at \(\pm \dfrac{\pi}{2}\), \(\pm \dfrac{3 \pi}{2}\)… The next thing to plot is the zeros which occur when the numerator, sine, is zero. This happens at \(0,\pm \pi ,\pm ,2\pi \ldots\) From the unit circle and basic right triangle trigonometry, you already know some values of \(\tan x\):
- \(\tan \dfrac{\pi }{4}=1\)
- \(\tan \left(−\dfrac{\pi }{4}\right)=−1\)
By plotting all this information, you get a very good sense as to what the graph of tangent looks like and you can fill in the rest.
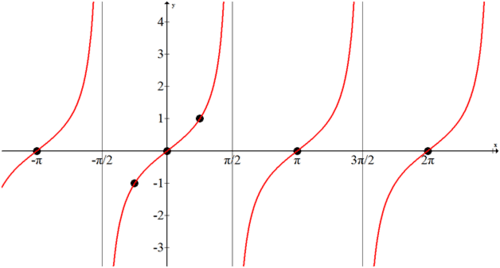
Notice that the period of tangent is \(\pi \) not \(2\pi \), because it has a shorter cycle.
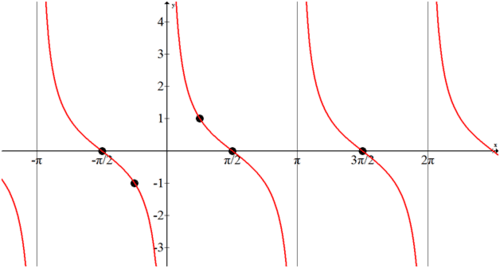
The graph of cotangent can be found using identical logic as tangent. You know \(\cot x=\dfrac{1}{\tan x}\). This means that the graph of cotangent will have zeros wherever tangent has asymptotes and asymptotes wherever tangent has zeroes. You also know that where tangent is 1, cotangent is also 1. Thus the graph of cotangent is:
Earlier, you were asked if the four new functions are transformations of sine and cosine.
Solution
The four new functions are not purely transformations of the sine and cosine functions. However, secant and cosecant are transformations of each other as are tangent and cotangent.
Graph the function \(f(x)=−2\cdot \csc (\pi (x−1))+1\).
Solution
Graph the function as if it were a sine function. Then insert asymptotes wherever the sine function crosses the sinusoidal axis. Lastly add in the cosecant curves.
The amplitude is 2. The shape is negative sine. The function is shifted up one unit and to the right one unit.
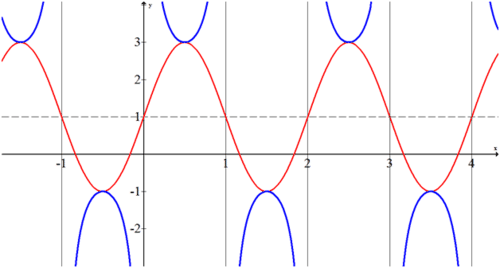
Note that only the blue portion of the graph represents the given function.
How do you write a tangent function as a cotangent function?
Solution
There are two main ways to go between a tangent function and a cotangent function. The first method was discussed in Example A: \(f(x)=\tan x=\dfrac{1}{\cot x}\).
The second approach involves two transformations. Start by reflecting across the x or the y axis. Notice that this produces an identical result. Next shift the function to the right or left by \(\dfrac{\pi}{2}\). Again this produces an identical result.
\(f(x)=\tan x=−\cot \left(x−\dfrac{\pi}{2}\right)\).
Find the equation of the function in the following graph.
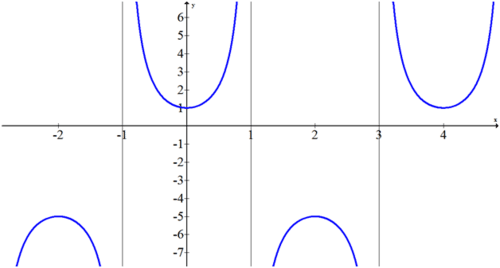
Solution
If you connect the relative maximums and minimums of the function, it produces a shifted cosine curve that is easier to work with.
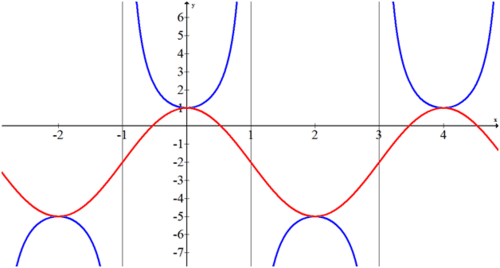
The amplitude is 3. The vertical shift is 2 down. The period is 4 which implies that \(b=\dfrac{\pi}{2}\). The shape is positive cosine and if you choose to start at x=0 there is no phase shift.
\(f(x)=3\cdot \csc \left(\dfrac{\pi}{2}x\right)−2\)
Where are the asymptotes for tangent and why do they occur?
Solution
Since \(\tan x=\dfrac{\sin x }{\cos x}\) the asymptotes occur whenever \(\cos x=0\) which is \(\pm \dfrac{\pi}{2},\pm \dfrac{3 \pi}{2}, \ldots\)
Review
1. What function can you use to help you make a sketch of \(f(x)=\sec x\)? Why?
2. What function can you use to help you make a sketch of \(g(x)=\csc x\)? Why?
Make a sketch of each of the following from memory.
- \(f(x)=\sec x\)
- \(g(x)=\csc x\)
- \(h(x)=\tan x\)
- \(k(x)=\cot x\)
Graph each of the following.
- \(f(x)=2\csc (x)+1\)
- \(g(x)=2\csc (\dfrac{\pi}{2}x)+1\)
- \(h(x)=2\csc \left(\dfrac{\pi }{2}(x−3)\right)+1\)
- \(j(x)=\cot \left(\dfrac{\pi }{2}x\right)+3\)
- \(k(x)=−\sec \left(\dfrac{\pi }{3}(x+1)\right)−4\)
- \(m(x)=−\tan (x)+1\)
- \(p(x)=−2\tan \left(x−\dfrac{\pi }{2}\right)+1\)
- Find two ways to write \(\sec x\) in terms of other trigonometric functions.
- Find two ways to write \(\csc x\) in terms of other trigonometric functions.
Review (Answers)
To see the Review answers, open this PDF file and look for \sec tion 5.7.
Vocabulary
| Term | Definition |
|---|---|
| Asymptotes | An asymptote is a line on the graph of a function representing a value toward which the function may approach, but does not reach (with certain exceptions). |
| Cosecant | The cosecant of an angle in a right triangle is a relationship found by dividing the length of the hypotenuse by the length of the side opposite to the given angle. This is the reciprocal of the sine function. |
| Cotangent | The cotangent of an angle in a right triangle is a relationship found by dividing the length of the side adjacent to the given angle by the length of the side opposite to the given angle. This is the reciprocal of the tangent function. |
| Secant | The secant of an angle in a right triangle is the value found by dividing length of the hypotenuse by the length of the side adjacent the given angle. The secant ratio is the reciprocal of the cosine ratio. |
| Transformations | Transformations are used to change the graph of a parent function into the graph of a more complex function. |
| Vertical Asymptote | A vertical asymptote is a vertical line marking a specific value toward which the graph of a function may approach, but will never reach. |

