4.1.1: Laws of Sines and Cosines
- Page ID
- 4154
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Solving for parts of non-right triangles using trigonometry.
Law of Sines: If \(\Delta ABC\) has sides of length, \(a\), \(b\), and \(c\), then \(\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\).
Looking at a triangle, the lengths a,b, and c are opposite the angles of the same letter.
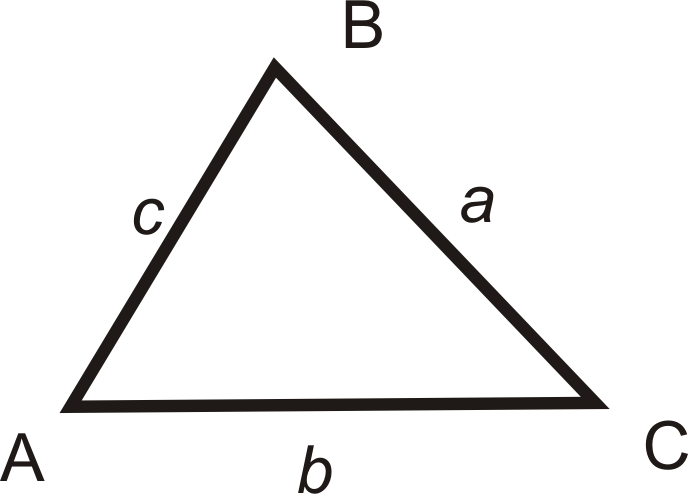
Use Law of Sines when given:
- An angle and its opposite side.
- Any two angles and one side.
Two sides and the non-included angle.
Law of Cosines: If \(\Delta ABC\) has sides of length \(a\),\(b\), and \(c\), then:
\(\begin{aligned} a^2&=b^2+c^2−2bc\cos A \\ b^2&=a^2+c^2−2ac \cos B \\ c^2&=a^2+b^2−2ab \cos C \end{aligned}\)
Even though there are three formulas, they are all very similar. First, notice that whatever angle is in the cosine, the opposite side is on the other side of the equal sign.
Use Law of Cosines when given:
- Two sides and the included angle.
- All three sides.
Using the Law of Sines
1. Solve the triangle using the Law of Sines. Round decimal answers to the nearest tenth.
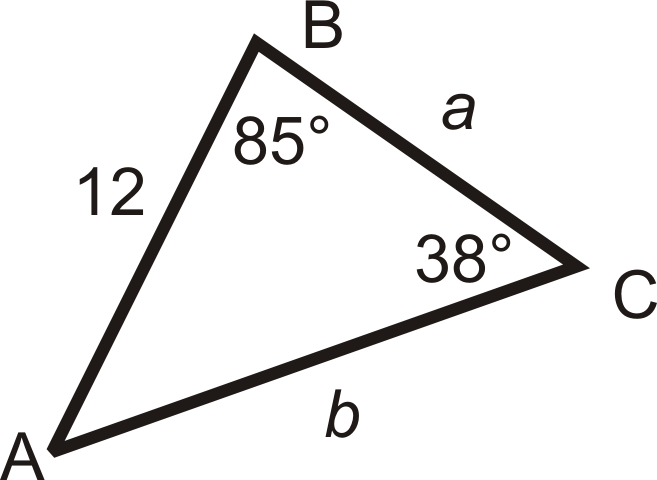
First, to find \(m\angle A\), we can use the Triangle Sum Theorem.
\(\begin{aligned} m\angle A+85^{\circ} +38^{\circ}&=180^{\circ} \\ m\angle A&=57^{\circ} \end{aligned}\)
Now, use the Law of Sines to set up ratios for \(a\) and \(b\).
\(\dfrac{\sin 57^{\circ} }{a}=\dfrac{\sin 85^{\circ} }{b}=\dfrac{\sin 38^{\circ} }{12}\)
\(\begin{aligned}
\dfrac{\sin 57^{\circ}}{a} &=\dfrac{\sin 38^{\circ}}{12} & \dfrac{\sin 85^{\circ}}{b} &=\dfrac{\sin 38^{\circ}}{12} \\
a \cdot \sin 38^{\circ} &=12 \cdot \sin 57^{\circ} & b \cdot \sin 38^{\circ} &=12 \cdot \sin 85^{\circ} \\
a &=\dfrac{12 \cdot \sin 57^{\circ}}{\sin 38^{\circ}} \approx 16.4 & \quad b &=\dfrac{12 \cdot \sin 85^{\circ}}{\sin 38^{\circ}} \approx 19.4
\end{aligned}\)
2. Solve the triangle using the Law of Sines. Round decimal answers to the nearest tenth.
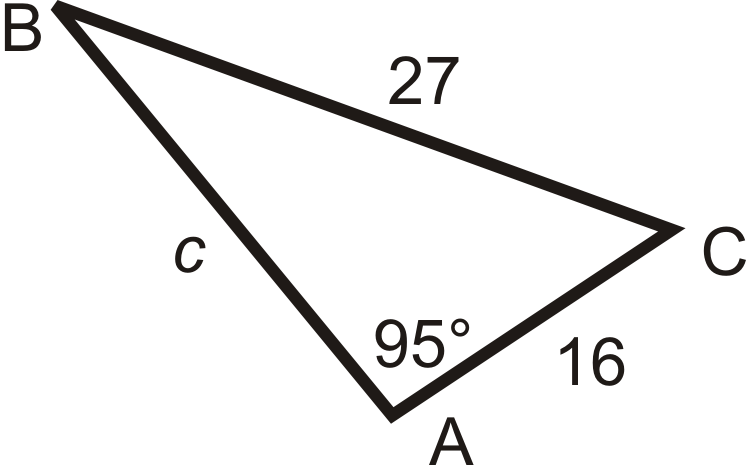
Set up the ratio for \(\angle B\) using Law of Sines.
\(\begin{aligned} \dfrac{\sin 95^{\circ} }{27}&=\dfrac{\sin B}{16} \\ 27\cdot \sin B&=16\cdot \sin 95^{\circ} \\ \sin B&=\dfrac{16\cdot \sin 95^{\circ} }{27}\rightarrow\sin ^{−1}\left(\dfrac{16\cdot \sin 95^{\circ} }{27} \right) =36.2^{\circ} \end{aligned}\)
To find \(m\angle C\) use the Triangle Sum Theorem.
\(m\angle C+95^{\circ} +36.2^{\circ} =180^{\circ} \rightarrow m\angle C=48.8^{\circ}\)
To find \(c\), use the Law of Sines again. \(\dfrac{\sin 95^{\circ} }{27}=\dfrac{\sin 48.8^{\circ} }{c}\)
\(\begin{aligned} c\cdot \sin 95^{\circ}&=27\cdot \sin 48.8^{\circ} \\ c&=27\cdot \sin 48.8^{\circ} \sin 95^{\circ} \approx 20.4 \end{aligned}\)
Using the Law of Cosines
Solve the triangle using Law of Cosines. Round your answers to the nearest hundredth.
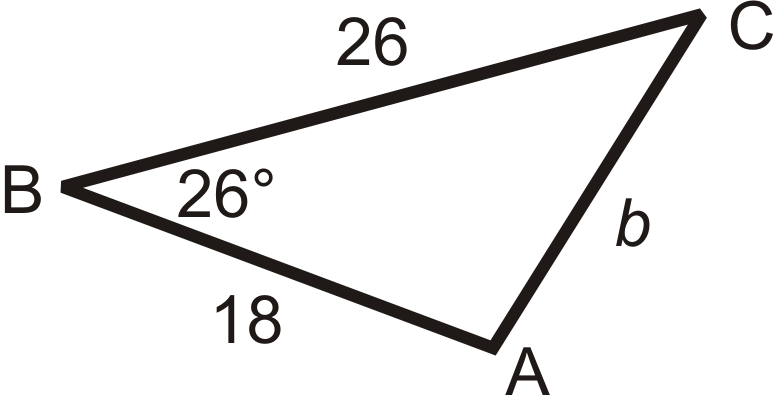
Use the second equation to solve for \(\angle B\).
\(\begin{aligned} b^2&=26^2+18^2−2(26)(18)\cos 26^{\circ} \\ b^2&=1000−936\cos 26^{\circ} \\ b^2&=158.7288 \\ b&\approx 12.60 \end{aligned}\)
To find \(m\angle A\) or \(m\angle C\), you can use either the Law of Sines or Law of Cosines. Let’s use the Law of Sines.
\(\begin{aligned} \dfrac{\sin 26^{\circ} }{12.60}&=\dfrac{\sin A}{18} \\ 12.60\cdot \sin A&=18\cdot \sin 26^{\circ} \\ \sin A&=18\cdot \sin 26^{\circ} 12.60 \end{aligned}\)
\(\sin ^{−1} \left(18\cdot \sin 26^{\circ} 12.60 \right)\approx 38.77^{\circ} \) To find \(m\angle C\), use the Triangle Sum Theorem.
\(\begin{aligned} 26^{\circ} +38.77^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=115.23^{\circ} \end{aligned}\)
Examples
Find the following angles in the triangle below. Round your answers to the nearest hundredth.
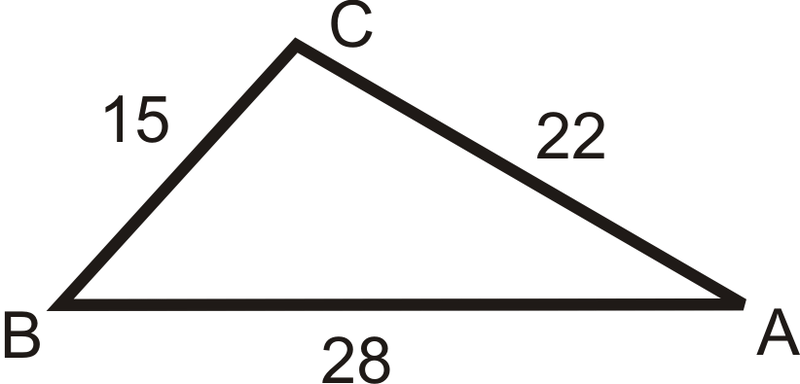
\(m\angle A\)
Solution
When you are given only the sides, you have to use the Law of Cosines to find one angle and then you can use the Law of Sines to find another.
\(\begin{aligned} 15^2&=22^2+28^2−2(22)(28)\cos A \\ 225&=1268−1232\cos A \\ −1043&=−1232\cos A \\ \dfrac{−1043}{−1232}&=\cos A \rightarrow \cos ^{−1}\left(\dfrac{1043}{1232}\right) \approx 32.16^{\circ}\end{aligned}\)
\(m\angle B\)
Solution
Now that we have an angle and its opposite side, we can use the Law of Sines.
\(\begin{aligned} \dfrac{\sin 32.16^{\circ} }{15} &=\dfrac{\sin B}{22} \\ 15\cdot \sin B &=22\cdot \sin 32.16^{\circ} \\ \sin B &=\dfrac{22\cdot \sin 32.16^{\circ} }{15} \end{aligned}\)
\(\sin ^{−1}\left(\dfrac{22\cdot \sin 32.16^{\circ} }{15}\right)\approx 51.32^{\circ} \).
\(m\angle C\)
Solution
To find \(m\angle C\), use the Triangle Sum Theorem.
\(\begin{aligned} 32.16^{\circ} +51.32^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=96.52^{\circ} \end{aligned}\)
Review
Use the Law of Sines or Cosines to solve \(\Delta ABC\). If you are not given a picture, draw one. Round all decimal answers to the nearest tenth.
-
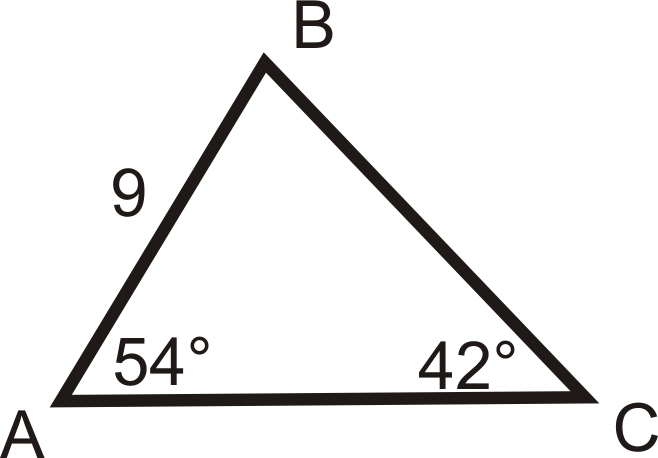
Figure \(\PageIndex{6}\) -
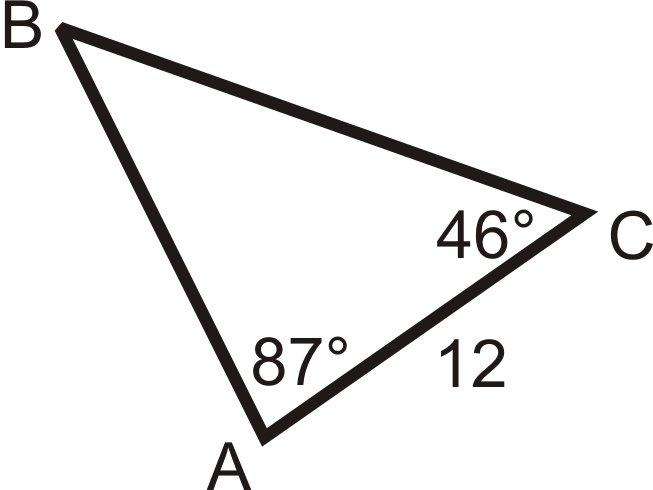
Figure \(\PageIndex{7}\) -
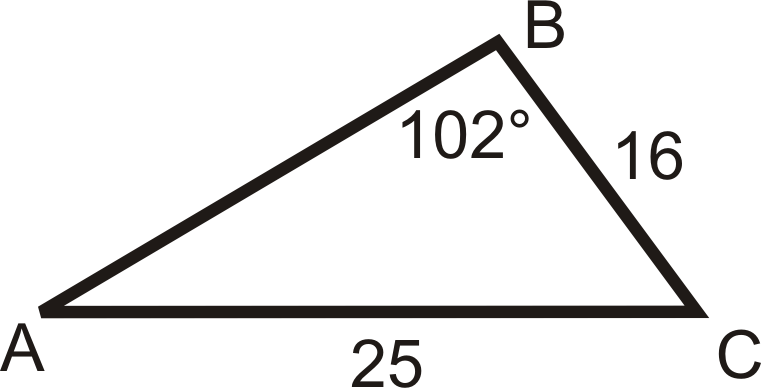
Figure \(\PageIndex{8}\) -
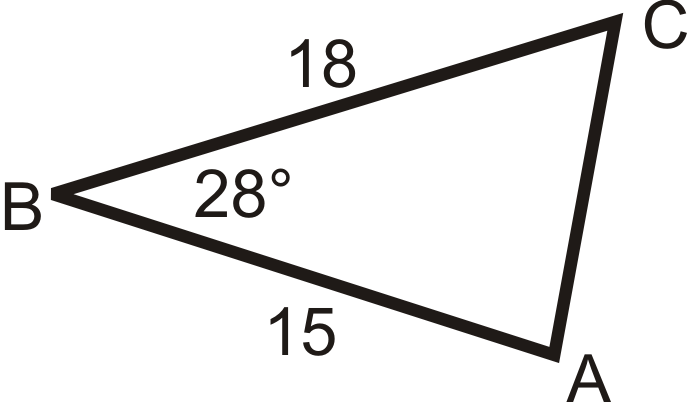
Figure \(\PageIndex{9}\) -
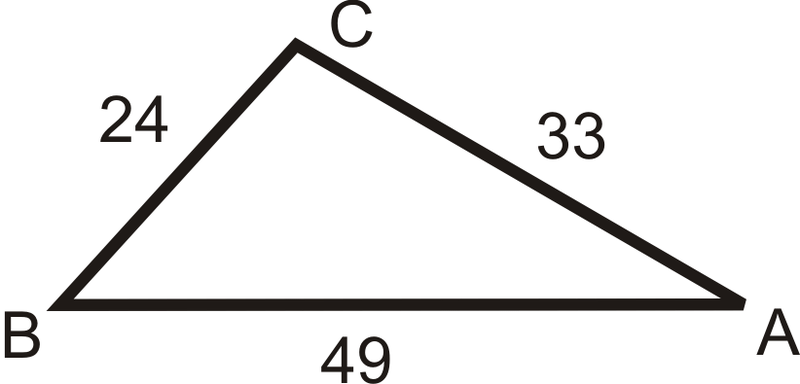
Figure \(\PageIndex{10}\) -
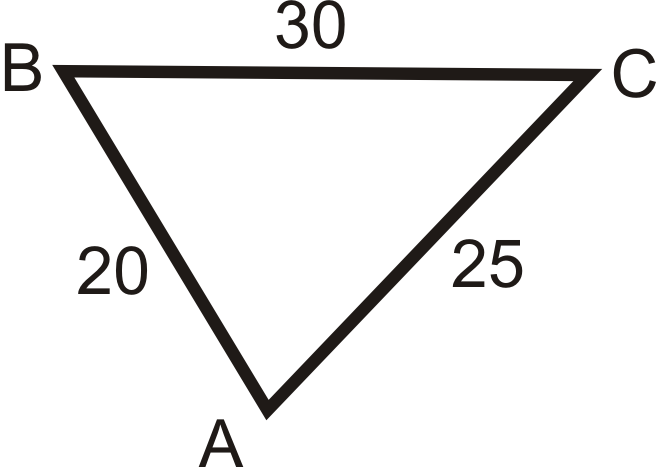
Figure \(\PageIndex{11}\) -
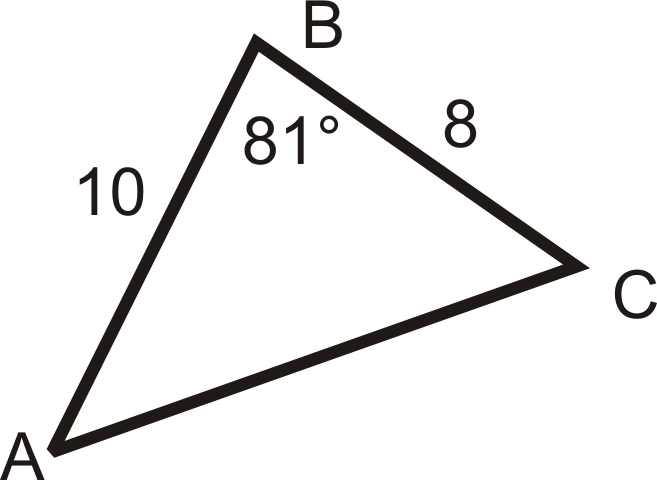
Figure \(\PageIndex{12}\) -
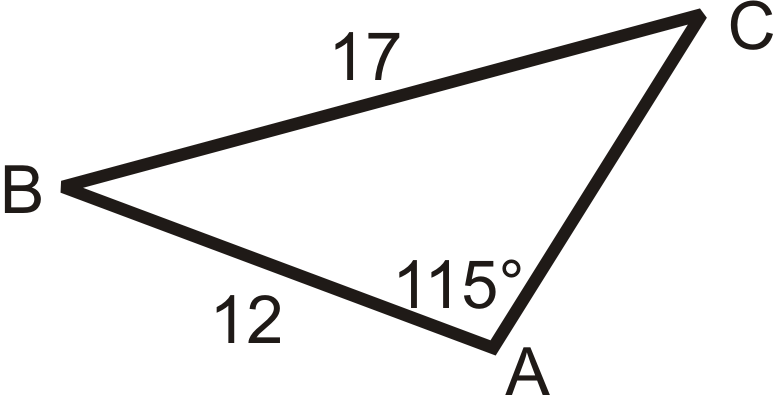
Figure \(\PageIndex{13}\) -
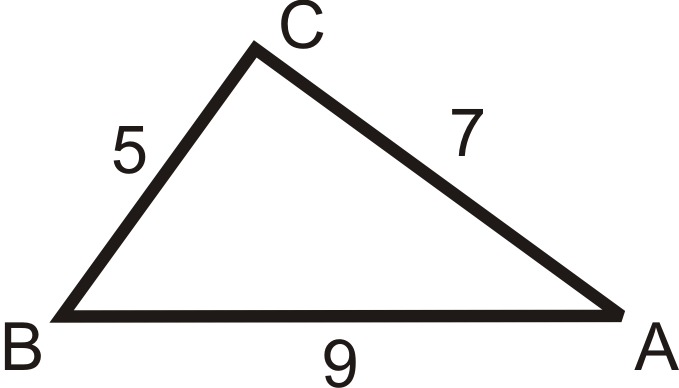
Figure \(\PageIndex{14}\) - \(m\angle A=74^{\circ} \), \(m\angle B=11^{\circ} \), \(BC=16\)
- \(m\angle A=64^{\circ} \), \(AB=29\), \(AC=34\)
- \(m\angle C=133^{\circ} \), \(m\angle B=25^{\circ} \),\(AB=48\)
Use the Law of Sines to solve \(\Delta ABC\) below.
- \(m\angle A=20^{\circ} \), \(AB=12\), \(BC=5\)
Recall that when we learned how to prove that triangles were congruent we determined that SSA (two sides and an angle not included) did not determine a unique triangle. When we are using the Law of Sines to solve a triangle and we are given two sides and the angle not included, we may have two possible triangles. Problem 14 illustrates this.
- Let’s say we have \(\Delta ABC\) as we did in problem 13. In problem 13 you were given two sides and the not included angle. This time, you have two angles and the side between them (ASA). Solve the triangle given that \(m\angle A=20^{\circ} \), \(m\angle C=125^{\circ}\), \(AC=8.4\)
- Does the triangle that you found in problem 14 meet the requirements of the given information in problem 13? How are the two different \(m\angle C\) related? Draw the two possible triangles overlapping to visualize this relationship.
Review (Answers)
To view the Review answers, open this PDF file and look for section 8.10.
Additional Resources
Video: The Law of Sines: The Basics

