4.1.2: Law of Sines
- Page ID
- 4153
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Proportion based on ratios of sides and sines of the opposite angles for non-right triangles.
When given a right triangle, you can use basic trigonometry to solve for missing information. When given SSS or SAS, you can use the Law of Cosines to solve for the missing information. But what happens when you are given two sides of a triangle and an angle that is not included? There are many ways to show two triangles are congruent, but SSA is not one of them. Why not?
The Law of Sines
When given two sides and an angle that is not included between the two sides, you can use the Law of Sines. The Law of Sines states that in every triangle the ratio of each side to the \sin e of its corresponding angle is always the same. Essentially, it clarifies the general concept that opposite the largest angle is always the longest side.
a\sin A=b\sin B=c\sin C
Here is a proof of the Law of Sines:
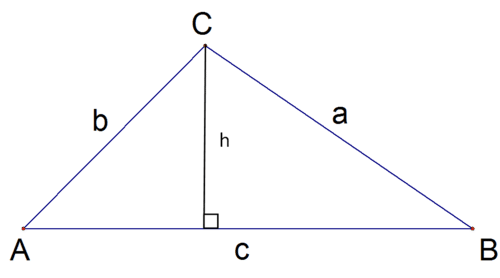
Looking at the right triangle formed on the left:
\(\begin{aligned} \sin A &=\dfrac{h}{b}\\ h&=b\sin A\end{aligned}\)
Looking at the right triangle formed on the right:
\(\begin{aligned} \sin B &=\dfrac{h}{a}\\ h&=a\sin B \end{aligned}\)
Equating the heights which must be identical:
\(\begin{aligned} a\sin B&=b\sin A \\ \dfrac{a}{\sin A}&=\dfrac{b}{\sin B} \end{aligned}\)
The best way to use the Law of Sines is to draw an extremely consistent picture each and every time even if that means redrawing and relabeling a picture. The reason why the consistency is important is because sometimes given SSA information defines zero, one or even two possible triangles.
Always draw the given angle in the bottom left with the two given sides above.
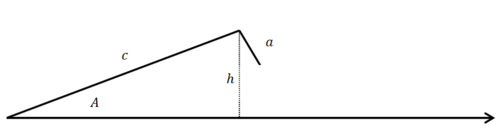
In this image side a is deliberately too short, but in most problems you will not know this. You will need to compare a to the height.
\(\begin{aligned} \sin A &=\dfrac{h}{c}\\ h&=c \sin A\end{aligned}\)
This is commonly referred to testing the ambiguous case. There are four different tests to determine the number of triangles that exist given the measurements.
Case 1: \(a<h\)
Simply put, side a is not long enough to reach the opposite side and constructing the triangle is impossible. Zero triangles exist.
Case 2: \(a=h\)
Side a just barely reaches the opposite side forming a 90^{\circ} angle.
Case 3: \(h<a<c\)
In this case side a can swing toward the interior of the triangle or the exterior of the triangle- there are two possible triangles. This is called the ambiguous case because the given information does not uniquely identify one triangle. To solve for both triangles, use the Law of Sines to solve for angle \(C_1\) first and then use the supplement to determine \(C_2\).
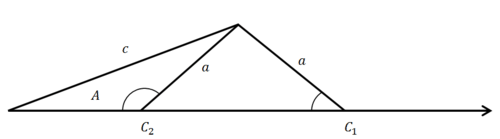
Case 4: \(c\leq a\)
In this case, side a can only swing towards the exterior of the triangle, only producing \(C_1\).
For the case of SSA, you should always check how many triangles there are before starting to find measures. Take the following triangle:
\(\angle A=40^{\circ}\), \(c=13\), and \(a=2\).
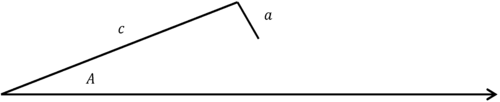
Before trying find \(\angle C\), you need to check that a triangle is possible and if there is more than one solution. Use the equation from above,
\(\begin{aligned} \sin 40^{\circ} &=\dfrac{h}{13}\\ h&=13\sin 40^{\circ}\approx 8.356 \end{aligned}\)
Because a<h (2<8.356), this information does not form a proper triangle.
Earlier, you were asked why SSA is not a method to show that two triangles are congruent.
Solution
SSA is not a method from Geometry that shows two triangles are congruent because it does not always define a unique triangle. Sometimes there is no triangle, one triangle, or two triangles.
\(\angle A=17^{\circ}\), \(c=14\), and \(a=4.0932 \ldots\) If possible, find \(\angle C\).

Solution
Check that a triangle is possible:
\(\begin{aligned} \sin 17^{\circ} &=\dfrac{h}{14}\\ h&=14 \sin 17^{\circ}\approx 4.0932 \end{aligned}\)
Since \(a=h\), this information forms exactly one triangle and angle C must be \(90^{\circ}\).
\(\angle A=22^{\circ}\), \(c=11\) and \(a=9\). If possible, find \(\angle C\).

Solution
Check that a triangle is possible:
\(\begin{aligned} \sin 22^{\circ} &=\dfrac{h}{11}\\ h&=11 \sin 22^{\circ}\approx 4.12 \end{aligned}\)
Since \(h<a<c\), there must be two possible angles for angle C.
Apply the Law of Sines:
\(\begin{aligned}
\frac{9}{\sin 22^{\circ}} &=\frac{11}{\sin C_{1}} \\
9 \sin C_{1} &=11 \sin 22^{\circ} \\
\sin C_{1} &=\frac{11 \sin 22^{\circ}}{9} \\
C_{1} &=\sin ^{-1}\left(\frac{11 \sin 22^{\circ}}{9}\right) \approx 27.24^{\circ} \\
C_{2} &=180-C_{1} \approx 152.75^{\circ}
\end{aligned}\)
Given \Delta ABC where A=12^{\circ}, \(B=50^{\circ}\), \(a=14 find b.
Solution
\(\begin{aligned} \dfrac{14}{\sin 12^{\circ}}&=\dfrac{b}{\sin 50^{\circ}} \\ b&=\dfrac{14\sin 50^{\circ}}{\sin 12^{\circ}}\approx 51.58\end{aligned}\)
Given \(\Delta ABC\) where \(A=70^{\circ}\), \(b=8\), \(a=3\), find \(\angle B\) if possible.
Solution
\(\begin{aligned} \sin 70^{\circ}&=\dfrac{h}{8} \\ h&=8\sin 70^{\circ}\approx 7.51 \ldots\end{aligned}\)
Because \(a<h\), this triangle is impossible.
Review
For 1-3, draw a picture of the triangle and state how many triangles could be formed with the given values.
- \(A=30^{\circ}\), \(a=13\), \(b=15\)
- \(A=22^{\circ}\), \(a=21\), \(b=12\)
- \(A=42^{\circ}\), \(a=36\), \(b=37\)
For 4-7, find all possible measures of \angle B (if any exist) for each of the following triangle values.
- \(A=86^{\circ}\), \(a=15\), \(b=11\)
- \(A=30^{\circ}\), \(a=24\), \(b=43\)
- \(A=48^{\circ}\), \(a=34\), \(b=39\)
- \(A=80^{\circ}\), \(a=22\), \(b=20\)
For 8-12, find the length of b for each of the following triangle values.
- \(A=94^{\circ}\), \(a=31\), \(B=34^{\circ}\)
- \(A=112^{\circ}\), \(a=12\), \(B=15^{\circ}\)
- \(A=78^{\circ}\), \(a=20\), \(B=16^{\circ}\)
- \(A=54^{\circ}\), \(a=15\), \(B=112^{\circ}\)
- \(A=39^{\circ}\), \(a=9\), \(B=98^{\circ}\)
- In \(\Delta ABC\), \(b=10\) and \(\angle A=39^{\circ}\). What's a possible value for a that would produce two triangles?
- In \(\Delta ABC\), \(b=10\) and \(\angle A=39^{\circ}\). What's a possible value for a that would produce no triangles?
- In \(\Delta ABC\), \(b=10\) and \(\angle A=39^{\circ}\). What's a possible value for a that would produce one triangle?
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.6.
Vocabulary
| Term | Definition |
|---|---|
| ambiguous | Ambiguous means that the given information is not specific. In the context of Geometry or Trigonometry, it means that the given data may not uniquely identify one shape. |
| SSA | SSA means side, side, angle and refers to the fact that two sides and the non-included angle of a triangle are known in a problem. |

