4.1.6: Law of Cosines

Find unknown side given two sides and included angle.

Sides of an Oblique Triangle

You are playing a game called ‘‘Over the Line’’, where you stand at one corner of a triangle and hit a ball. The field looks like this:

Figure \(\PageIndex{1}\)

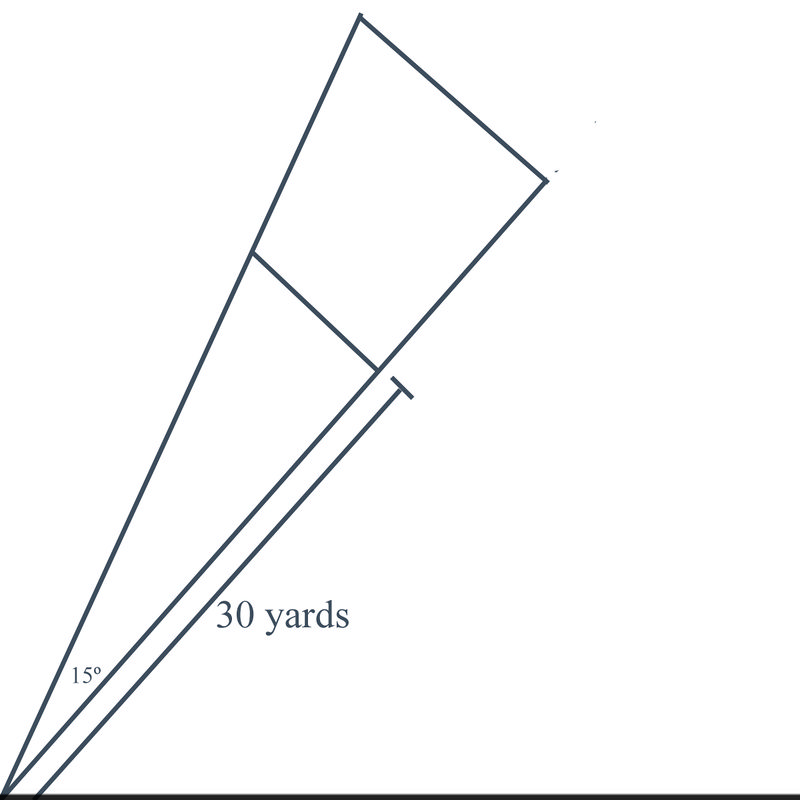
Points are scored by hitting the ball so that it lands beyond the first line in the triangle, but before the second line.

Given that the angle on the left hand side of the triangle is \(15^{\circ}\), and the length of the sides of the triangle going to the first scoring line are 30 yards, can you calculate the length of the line you have to hit the ball past to score?

Finding the Sides of an Oblique Triangle

This lesson takes ideas that have only been applied to right triangles and interprets them so that they can be used for any type of triangle.

First, the laws of sines and cosines take the Pythagorean Theorem and ratios and apply them to any triangle.

The Law of Cosines is a generalization of the Pythagorean Theorem, where the angle C is the angle between the two given sides of a triangle:

\(c^2=a^2+b^2−2(a)(b)\cos C\)

You'll notice that if this were a right triangle, \(\cos C=\cos 90^{\circ}=0\), and so the third term would disappear, leaving the familiar Pythagorean Theorem.

One case where we can use the Law of Cosines is when we know two sides and the included angle in a triangle (SAS) and want to find the third side.

Solving for Unknown Values

1. Using \(\Delta DEF\), \(\angle E=12^{\circ}\), \(d=18\), and \(f=16.8\). Find \(e\).

Figure \(\PageIndex{2}\)

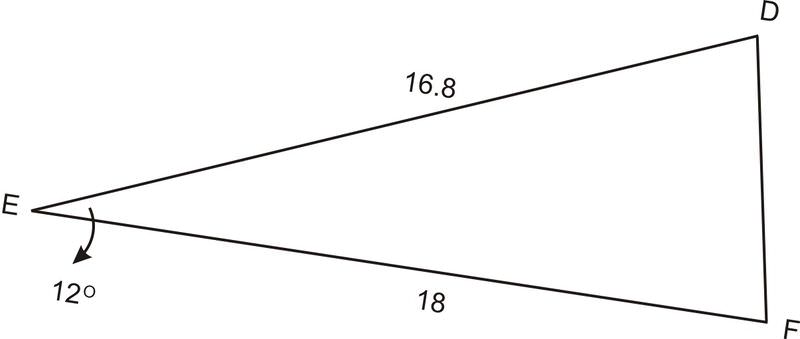
Since \(\Delta DEF\) isn’t a right triangle, we cannot use the Pythagorean Theorem or trigonometry functions to find the third side. However, we can use our newly derived Law of Cosines.

\(\begin{aligned} e^2&=18^2+16.8^2−2(18)(16.8)\cos 12 && \text{ Law of Cosines} \\ e^2 &=324+282.24−2(18)(16.8)\cos 12 && \text{ Simplify squares} \\ e^2&=324+282.24−591.5836689 && \text{ Multiply} \\ e^2&=14.6563311 && \text{ Add and subtract from left to right} \\ e&\approx 3.8 && \text{ Square root} \end{aligned}\)

∗Note that the negative answer is thrown out as having no geometric meaning in this case.

2. An architect is designing a kitchen for a client. When designing a kitchen, the architect must pay special attention to the placement of the stove, sink, and refrigerator. In order for a kitchen to be utilized effectively, these three amenities must form a triangle with each other. This is known as the “work triangle.” By design, the three parts of the work triangle must be no less than 3 feet apart and no more than 7 feet apart. Based on the dimensions of the current kitchen, the architect has determined that the sink will be 3.6 feet away from the stove and 5.7 feet away from the refrigerator. If the sink forms a \(103^{\circ}\) angle with the stove and the refrigerator, will the distance between the stove and the refrigerator remain within the confines of the work triangle?

Figure \(\PageIndex{3}\)

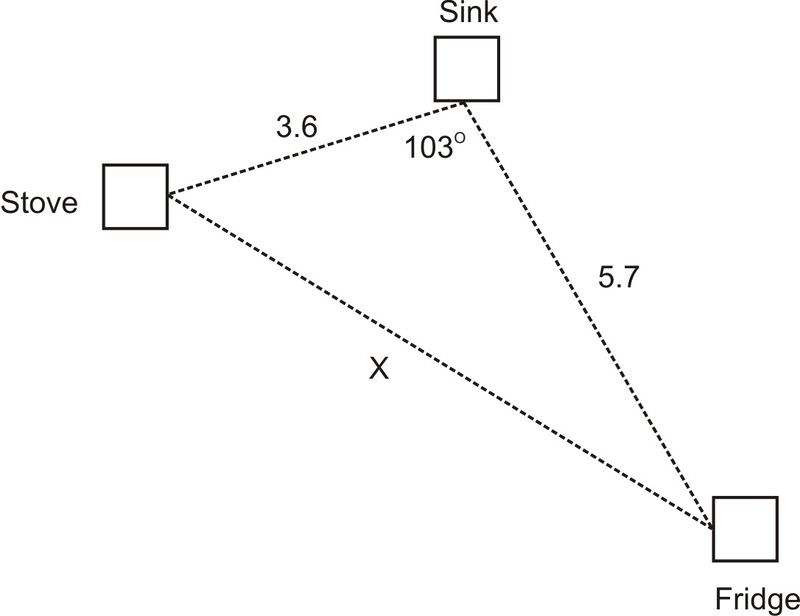
In order to find the distance from the sink to the refrigerator, we need to find side \(x\). To find side \(x\), we will use the Law of Cosines because we are dealing with an obtuse triangle (and thus have no right angles to work with). We know the length two sides: the sink to the stove and the sink to the refrigerator. We also know the included angle (the angle between the two known lengths) is \(103^{\circ}\). This means we have the SAS case and can apply the Law of Cosines.

\(\begin{aligned} x^2 &=3.6^2+5.7^2−2(3.6)(5.7)\cos 103 && \text{ Law of Cosines} \\ x^2 &=12.96+32.49−2(3.6)(5.7)\cos 103 && \text{ Simplify squares} \\ x^2 &=12.96+32.49+9.23199127 && \text{ Multiply} \\ x^2 &=54.68199127 && \text{ Evaluate} \\ x &\approx 7.4 && \text{ Square root} \end{aligned}\)

No, this triangle does not conform to the definition of a work triangle. The sink and the refrigerator are too far apart by 0.4 feet.Solve for \(j\).

3. Using \(\Delta JKL\), \(\angle J=2^{\circ}\), \(l=25\), and \(k=27\). Find \(j\).

Since \(\Delta JKL\) isn’t a right triangle, we cannot use the Pythagorean Theorem or trigonometry functions to find the third side. However, we can use our newly derived Law of Cosines.

\(\begin{aligned} j^2 &=25^2+27^2−2(25)(27)\cos 2 && \text{ Law of Cosines} \\ j^2&=625+729−2(25)(27)\cos 2 && \text{ Simplify squares} \\ j^2 &=625+729−1349.18 && \text{ Multiply} \\ j^2&=4.82 && \text{ Add and subtract from left to right} \\ j &\approx 2.20 && \text{ Square root} \end{aligned}\)

∗Note that the negative answer is thrown out as having no geometric meaning in this case.

Example \(\PageIndex{1}\)

Earlier, you were asked to calculate the length of the line you have to hit the ball past to score.

Solution

Since you know that the length of each of the other 2 sides is 30 yards, and the angle is \(15^{\circ}\), you can use the Law of Cosines to find the length of the third side.

\(\begin{aligned} c^2&=a^2+b^2−2ab\cos \theta \\ c^2&=30^2+30^2−(2)(30)(30)\cos 15^{\circ} \\ c^2&=900+900−1738.67 \\ c^2&=1800−1738.67 \\ c^2&=61.33c\approx 7.83 \end{aligned}\)

Example \(\PageIndex{2}\)

Find side "\(a\)" in this triangle, where \(\angle A=50^{\circ}\), \(b=8\), \(c=11\)

Figure \(\PageIndex{4}\)

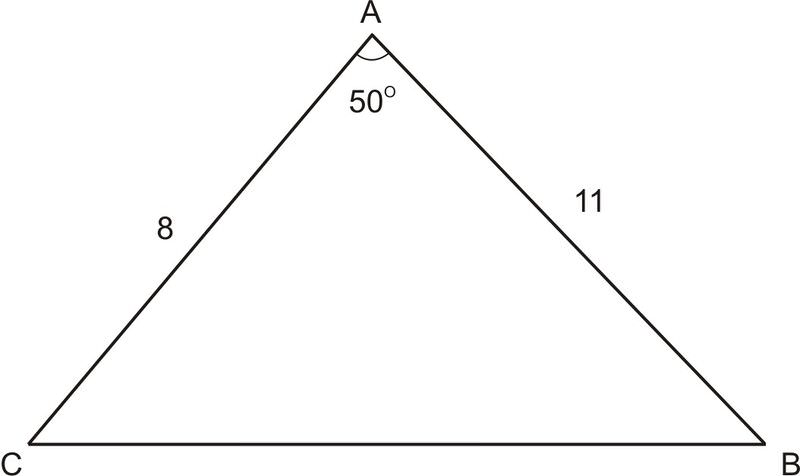
Solution

\(a^2=8^2+11^2−2\cdot 8\cdot 11\cdot \cos 50^{\circ}\), \(a\approx 8.5\)

Example \(\PageIndex{3}\)

Find side "\(l\)" in this triangle where \(\angle L=79.5^{\circ}\), \(m=22.4\), \(p=13.17\)

Figure \(\PageIndex{5}\)

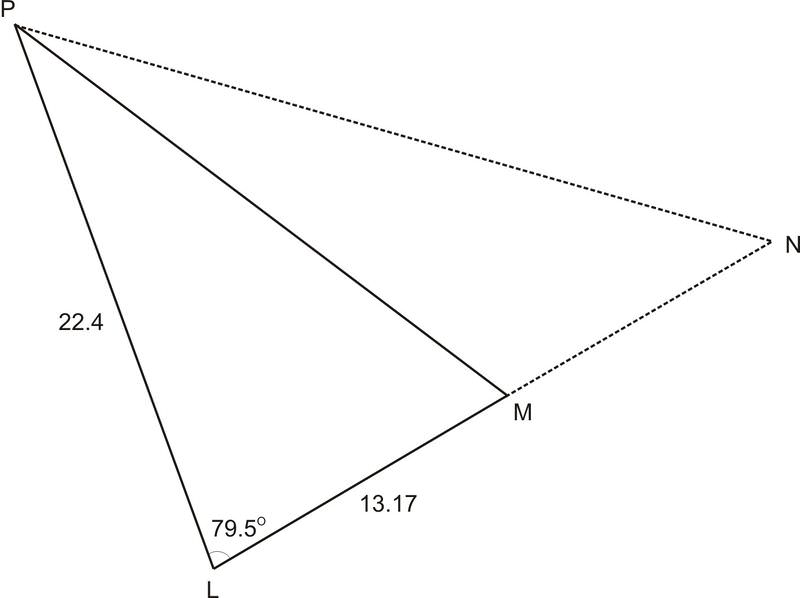
Solution

\(l^2=22.4^2+13.17^2−2\cdot 22.4\cdot 13.17\cdot \cos 79.5^{\circ}\), \(l\approx 23.8\)

Example \(\PageIndex{4}\)

Find side "\(b\)" in this triangle where \(\angle B=67.2^{\circ}\), \(d=43\), \(e=39\)

Figure \(\PageIndex{6}\)

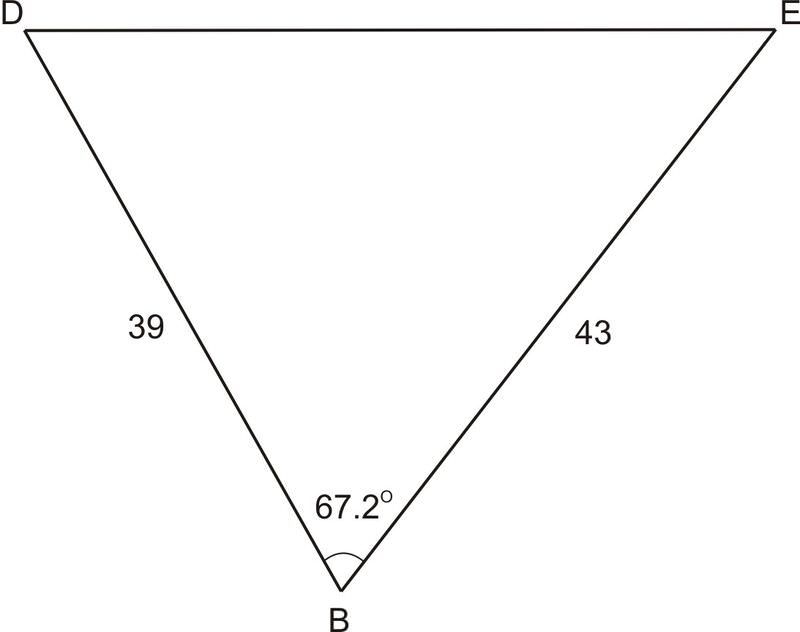
Solution

\(b^2=39^2+43^2−2\cdot 39\cdot 43\cdot \cos 67.2^{\circ}\), \(b\approx 45.5\)

Review

1. State the Law of Cosines.

For each triangle below, state the values of \(a\), \(b\), and \(c\).

2. 
   

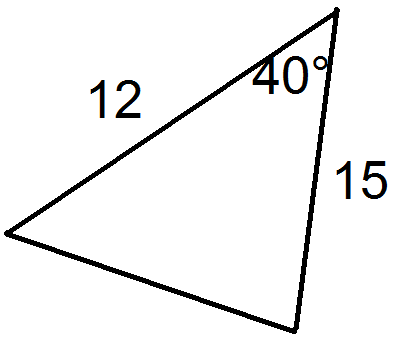
   Figure \(\PageIndex{7}\)

3. 
   

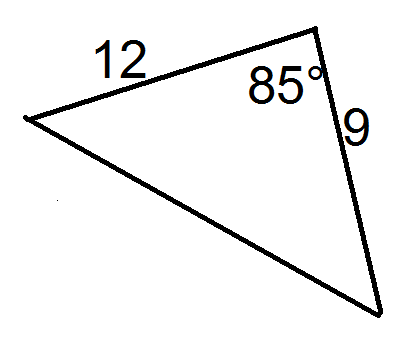
   Figure \(\PageIndex{8}\)

4. 
   

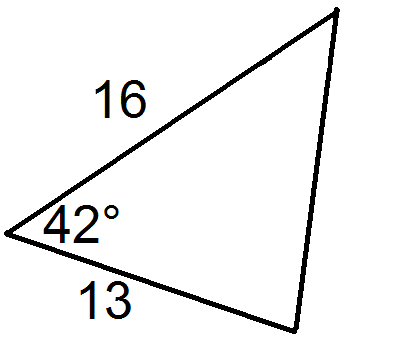
   Figure \(\PageIndex{9}\)

5. 
   

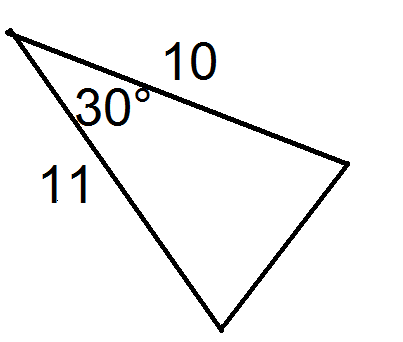
   Figure \(\PageIndex{10}\)

6. 
   

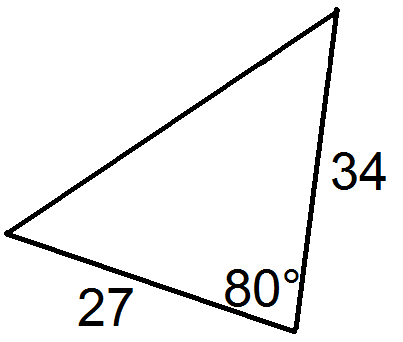
   Figure \(\PageIndex{11}\)

7. 
   

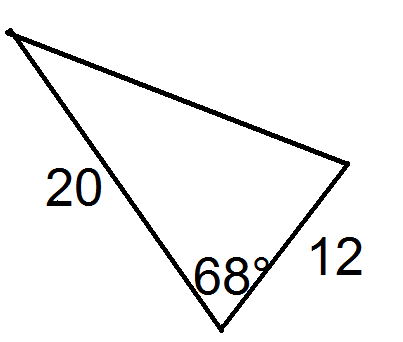
   Figure \(\PageIndex{12}\)

8. 
   

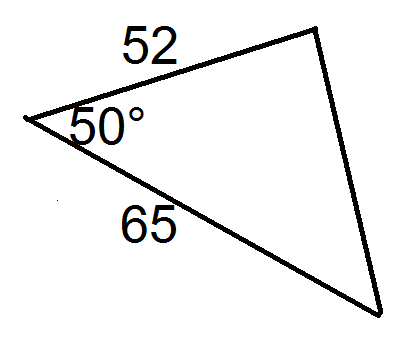
   Figure \(\PageIndex{13}\)

Now, for each triangle, solve for the missing side using the Law of Cosines.

9. 
   

   Figure \(\PageIndex{14}\)

10. 
    

    Figure \(\PageIndex{15}\)

11. 
    

    Figure \(\PageIndex{16}\)

12. 
    

    Figure \(\PageIndex{17}\)

13. 
    

    Figure \(\PageIndex{18}\)

14. 
    

    Figure \(\PageIndex{19}\)

15. 
    

    Figure \(\PageIndex{20}\)

16. Prove that the Law of Cosines is equivalent to the Pythagorean Theorem for all right triangles.

Review (Answers)

To see the Review answers, open this PDF file and look for section 5.1.

Vocabulary

Term	Definition
Included Angle	The included angle in a triangle is the angle between two known sides.
law of cosines	The law of cosines is a rule relating the sides of a triangle to the cosine of one of its angles. The law of cosines states that \(c^2=a^2+b^2−2ab\cos C\), where \(C\) is the angle across from side \(c\).
Oblique Triangle	An oblique triangle is a triangle without a right angle as one of its internal angles.
Side Angle Side Triangle	A side angle side triangle is a triangle where two of the sides and the angle between them are known quantities.

Additional Resources

Video: Example: Application of the Law of Cosine

Practice: Law of Cosines