4.14: SAS
- Page ID
- 4811
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two sets of corresponding sides and included angles prove congruent triangles.
Side-Angle-Side Postulate
If two sides and the included angle in one triangle are congruent to two sides and the included angle in another triangle, then the two triangles are congruent. (When an angle is between two given sides of a polygon it is called an included angle.)
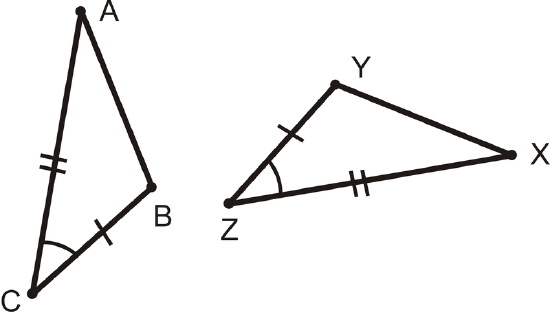
\(\overline{AC}\cong \overline{XZ}\), \(\overline{BC}\cong YZ\), and \(\angle C\cong \angle Z\), then \(\Delta ABC\cong \Delta XYZ\).
This is called the Side-Angle-Side (SAS) Postulate and it is a shortcut for proving that two triangles are congruent. The placement of the word Angle is important because it indicates that the angle you are given is between the two sides.
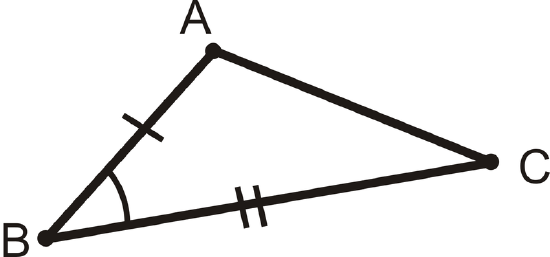
\(\angle B\) would be the included angle for sides \(\overline{AB}\) and \(\overline{BC}\).
What if you were given two triangles and provided with only two of their side lengths and the measure of the angle between those two sides? How could you determine if the two triangles were congruent?
Example \(\PageIndex{1}\)
Is the pair of triangles congruent? If so, write the congruence statement and why.
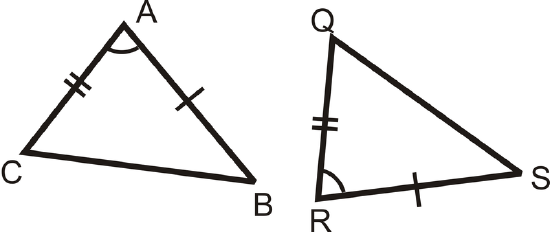
Solution
The pair of triangles is congruent by the SAS postulate. \(\Delta CAB\cong \Delta QRS\).
Example \(\PageIndex{2}\)
State the additional piece of information needed to show that each pair of triangles is congruent.
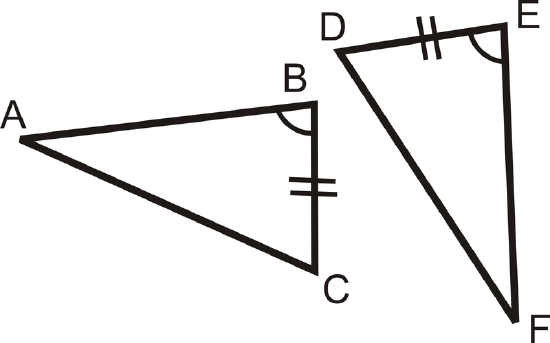
Solution
We know that one pair of sides and one pair of angles are congruent from the diagram. In order to know that the triangles are congruent by SAS we need to know that the pair of sides on the other side of the angle are congruent. So, we need to know that \(\overline{EF}\cong \overline{BA}\).
Example \(\PageIndex{3}\)
Fill in the blanks in the proof below.
Given:
\(\overline{AB}\cong \overline{DC},\: \overline{BE}\cong \overline{CE}\)
Prove: \(\Delta ABE\cong \Delta ACE\)
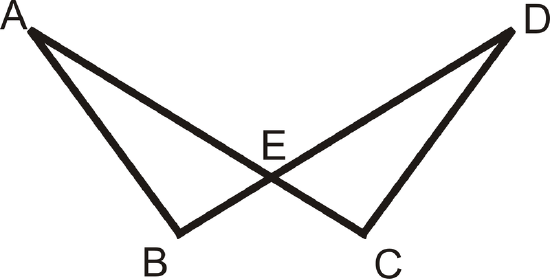
Solution
| Statement | Reason |
|---|---|
| 1. | 1. |
| 2. \(\angle AEB\cong \angle DEC\) | 2. |
| 3. \(\Delta ABE\cong \Delta ACE\) | 3. |
| Statement | Reason |
|---|---|
| 1. \(\overline{AB}\cong \overline{DC},\: \overline{BE}\cong \overline{CE}\) | 1. Given |
| 2. \(\angle AEB\cong \angle DEC\) | 2. Vertical Angle Theorem |
| 3. \(\Delta ABE\cong \Delta ACE\) | 3. SAS postulate |
Example \(\PageIndex{4}\)
What additional piece of information do you need to show that these two triangles are congruent using the SAS Postulate, \(\angle ABC\cong \angle LKM\), \(\overline{AB}\cong LK\overline{AB}\), \(\overline{BC}\cong \overline{KM}\), or \(\angle BAC\cong \angle KLM\)?
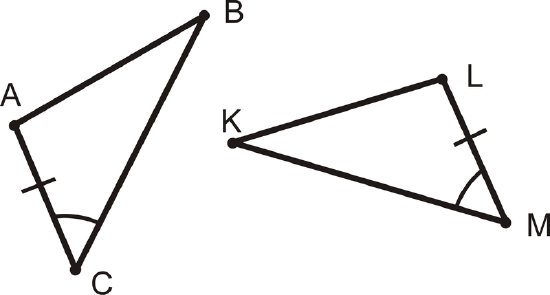
Solution
For the SAS Postulate, you need the side on the other side of the angle. In \(\Delta ABC\), that is \(\overline{BC}\) and in \(\Delta LKM\) that is \(\overline{KM}\). The answer is \(\overline{BC}\cong \overline{KM}\).
Example \(\PageIndex{5}\)
Is the pair of triangles congruent? If so, write the congruence statement and why.
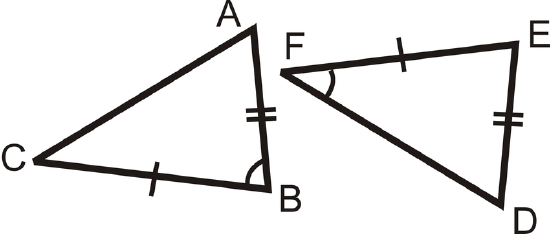
Solution
While the triangles have two pairs of sides and one pair of angles that are congruent, the angle is not in the same place in both triangles. The first triangle fits with SAS, but the second triangle is SSA. There is not enough information for us to know whether or not these triangles are congruent.
Review
Are the pairs of triangles congruent? If so, write the congruence statement and why.
-
Figure \(\PageIndex{7}\) -
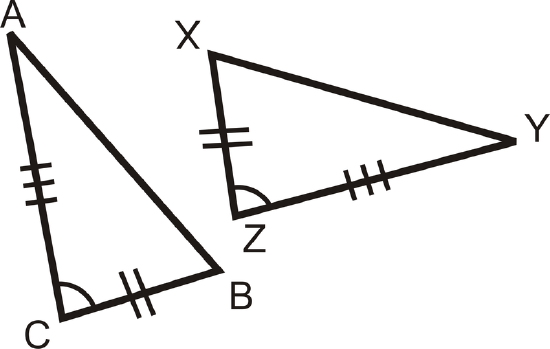
Figure \(\PageIndex{7}\) -
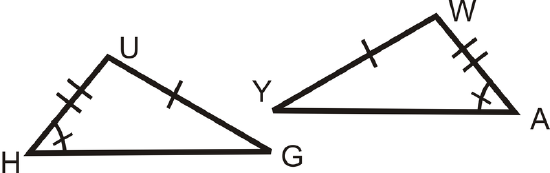
Figure \(\PageIndex{7}\)
State the additional piece of information needed to show that each pair of triangles is congruent by SAS.
-
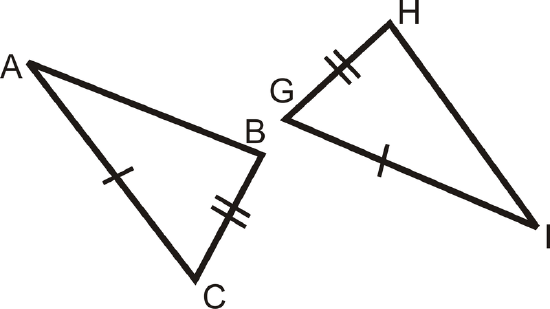
Figure \(\PageIndex{7}\) -
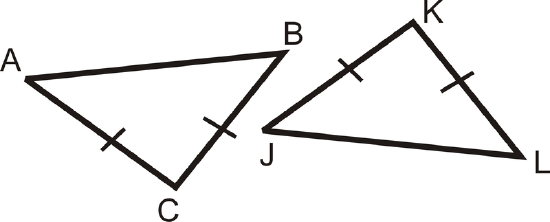
Figure \(\PageIndex{7}\) -
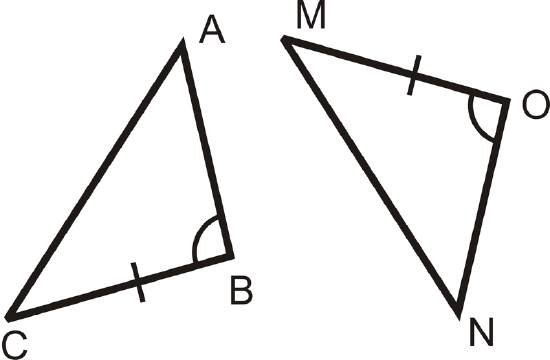
Figure \(\PageIndex{7}\)
Fill in the blanks in the proofs below.
- Given:
- \(B\) is a midpoint of \(\overline{DC}\)
- \(\overline{AB}\perp \overline{DC}\)
Prove: \(\Delta ABD\cong \Delta ABC \)
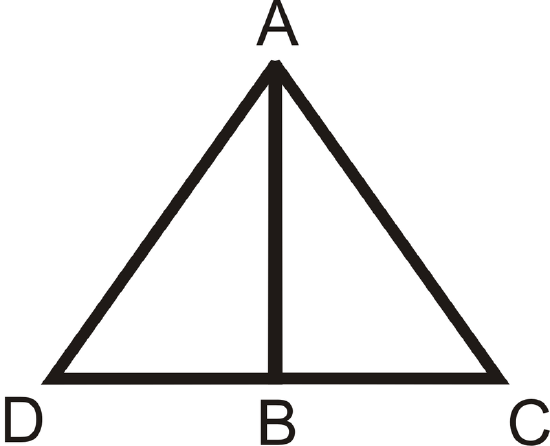
Figure \(\PageIndex{8}\)
| Statement | Reason |
|---|---|
| 1. \(B\) is a midpoint of \(\overline{DC},\: \overline{AB}\perp \overline{DC}\) | 1. |
| 2. | 2. Definition of a midpoint |
| 3. \(\angle ABD\) and \(\angle ABC\) are right angles | 3. |
| 4. | 4. All right angles are \cong\) |
| 5. | 5. |
| 6. \(\Delta ABD\cong \Delta ABC\) | 6. |
- Given:
- \(\overline{AB}\) is an angle bisector of \(\angle DAC\)
- \(\overline{AD}\cong \overline{AC}\)
Prove: \(\Delta ABD\cong \Delta ABC \)

Figure \(\PageIndex{9}\)
| Statement | Reason |
|---|---|
| 1. | 1. |
| 2. \(\angle DAB\cong \angle BAC\) | 2. |
| 3. | 3. Reflexive \(PoC\) |
| 4. \(\Delta ABD\cong \Delta ABC\) | 4. |
- Given:
- \(B\) is the midpoint of\( \overline{DE}\) and \(\overline{AC}\)
- \(\angle ABE\) is a right angle
Prove: \(\Delta ABE\cong \Delta CBD \)
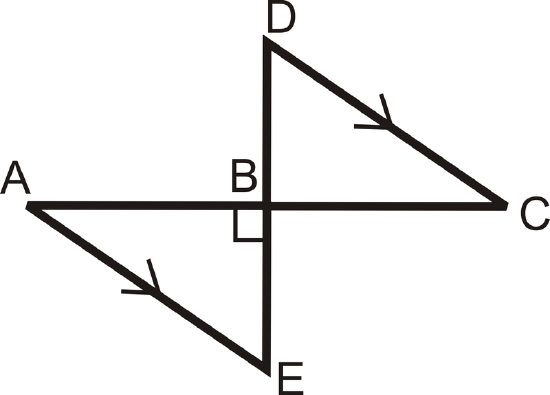
Figure \(\PageIndex{10}\)
| Statement | Reason |
|---|---|
| 1. | 1. Given |
| 2. \(\overline{DB}\cong \overline{BE},\: \overline{AB}\cong \overline{BC}\) | 2. |
| 3. | 3. Definition of a Right Angle |
| 4. | 4. Vertical Angle Theorem |
| 5. \(\Delta ABE\cong \Delta CBD\) | 5. |
- Given:
- \(\overline{DB}\) is the angle bisector of \(\angle ADC\)
- \(\overline{AD}\cong \overline{DC}\)
Prove: \(\Delta ABD\cong \Delta CBD\)
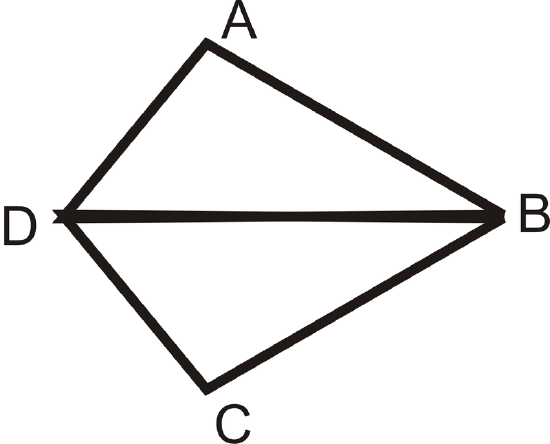
Figure \(\PageIndex{11}\)
| Statement | Reason |
|---|---|
| 1. | 1. |
| 2. \(\angle ADB \cong \angle BDC\) | 2. |
| 3. | 3. |
| 4. \(\Delta ABD\cong \Delta CBD\) | 4. |
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.7.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Base Angles | The base angles of an isosceles triangle are the angles formed by the base and one leg of the triangle. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Equilateral Triangle | An equilateral triangle is a triangle in which all three sides are the same length. |
| Included Angle | The included angle in a triangle is the angle between two known sides. |
| SAS | SAS means side, angle, side, and refers to the fact that two sides and the included angle of a triangle are known. |
| Side Angle Side Triangle | A side angle side triangle is a triangle where two of the sides and the angle between them are known quantities. |
| Triangle Congruence | Triangle congruence occurs if 3 sides in one triangle are congruent to 3 sides in another triangle. |
| Rigid Transformation | A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure. |
Additional Resources
Interactive Element
Video: Introduction to Congruent Triangles
Activities: SAS Triangle Congruence Discussion Questions
Study Aids: Triangle Congruence Study Guide
Practice: SAS
Real World: SSS Triangle Congruence

