4.13: SSS
- Page ID
- 4809
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Three sets of equal side lengths determine congruence.
Side-Side-Side Postulate
If 3 sides in one triangle are congruent to 3 sides in another triangle, then the triangles are congruent.
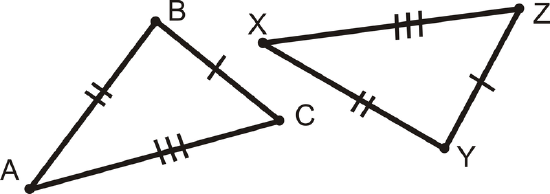
\(\overline{BC}\cong \overline{YZ}\), \(\overline{AB}\cong \overline{XY}\), and \(\overline{AB}\cong \overline{XZ}\) then \(\Delta ABC \cong \Delta XYZ\).
This is called the Side-Side-Side (SSS) Postulate and it is a shortcut for proving that two triangles are congruent. Before, you had to show 3 sides and 3 angles in one triangle were congruent to 3 sides and 3 angles in another triangle. Now you only have to show 3 sides in one triangle are congruent to 3 sides in another.
What if you were given two triangles and provided with information only about their side lengths? How could you determine if the two triangles were congruent?
Example \(\PageIndex{1}\)
Determine if the two triangles are congruent.
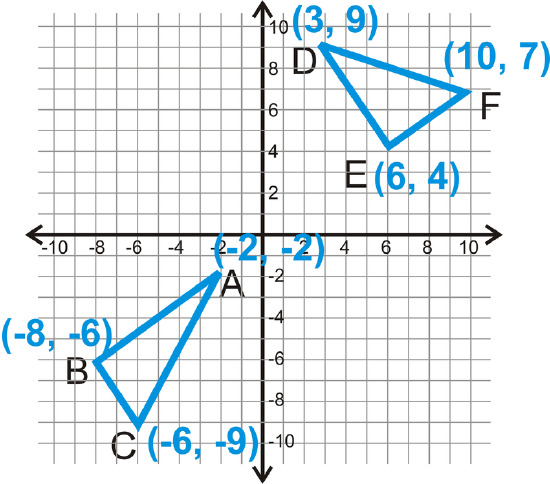
Solution
Start with \(\Delta ABC\).
\(\begin{align*} AB &=\sqrt{(−2−(−8))^2+(−2−(−6))^2}\\ &=\sqrt{(6)^2+(4)^2}\\ &=\sqrt{36+16}\\ &=\sqrt{52}\\ &=\sqrt{213} \\ BC&=\sqrt{(−8−(−6))^2+(−6−(−9))^2}\\ &=\sqrt{(−2)^2+(3)^2}\\ &=\sqrt{4+9}\\ &=\sqrt{13} \\ AC&=\sqrt{(−2−(−6))^2+(−2−(−9))^2}\\ &=\sqrt{(4)^2+(7)^2}\\ &=\sqrt{16+49}\\ &=\sqrt{65} \end{align*} \)
Now find the sides of \(\Delta DEF\).
\(\begin{align*} DE &=\sqrt{(3−6)^2+(9−4)^2}\\ &=\sqrt{(−3)^2+(5)^2}\\ &=\sqrt{9+25}\\ &=\sqrt{34} \\ EF&=\sqrt{(6−10)^2+(4−7)^2}\\ &=\sqrt{(−4)^2+(−3)^2}\\ &=\sqrt{16+9}\\ &=\sqrt{25}\\ &=5 \\ DF&=\sqrt{(3−10)^2+(9−7)^2}\\ &=\sqrt{(−7)^2+(2)^2}\\ &=\sqrt{49+4}\\ &=\sqrt{53} \end{align*}\)
No sides have equal measures, so the triangles are not congruent.
Example \(\PageIndex{2}\)
Fill in the blanks in the proof below.
Given:\( \overline{AB}\cong \overline{DC}\), \(\overline{AC}\cong \overline{DB}\)
Prove: \(\Delta ABC\cong \Delta DCB\)
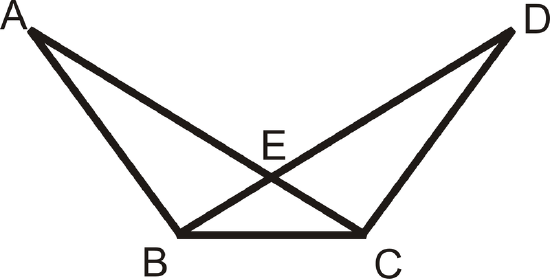Figure \(\PageIndex{4}\)Solution
| Statement | Reason |
|---|---|
| 1. | 1. |
| 2. | 2. Reflexive \(PoC\) |
| 3. \(\Delta ABC\cong \Delta DCB\) | 3. |
| Statement | Reason |
|---|---|
| 1. \(\overline{AB}\cong \overline{DC}, \overline{AC}\cong \overline{DB}\) | 1. Given |
| 2. \(\overline{BC}\cong \overline{CB}\) | 2. Reflexive \(PoC\) |
| 3. \(\Delta ABC\cong \Delta DCB\) | 3. SSS Postulate |
Example \(\PageIndex{3}\)
Write a triangle congruence statement based on the picture below:
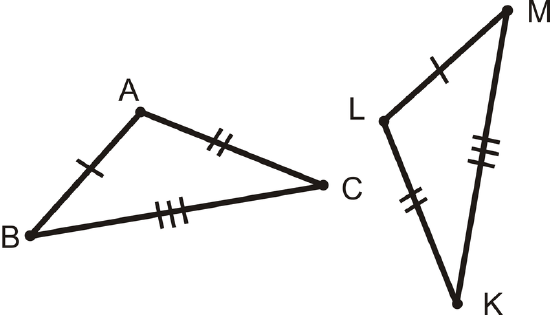Figure \(\PageIndex{5}\)Solution
From the tic marks, we know AB\overline{AB}\cong LM\overline{AB}\), AC\overline{AB}\cong LK\overline{AB}\), \overline{BC}\cong MK\overline{AB}\). From the SSS Postulate, the triangles are congruent. Lining up the corresponding sides, we have \Delta ABC\cong \Delta LMK\).
Don’t forget ORDER MATTERS when writing congruence statements. Line up the sides with the same number of tic marks.
Example \(\PageIndex{4}\)
Write a two-column proof to show that the two triangles are congruent.
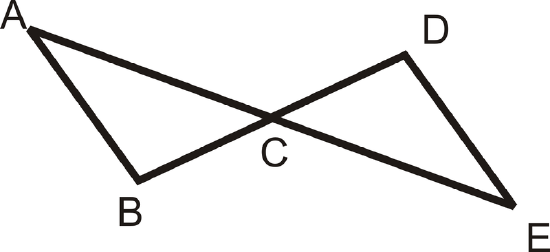Figure \(\PageIndex{6}\)Given: \(\overline{AB}\cong \overline{DE}\)
\(C\) is the midpoint of \(\overline{AE}\) and \(\overline{DB}\).
Prove: \(\Delta ACB\cong \Delta ECD\)
Solution
| Statement | Reason |
|---|---|
|
1. \(\overline{AB}\cong \overline{DE}\) \(C\) is the midpoint of \(\overline{AE} and \(\overline{DB}\) |
1.Given |
| 2. \(\overline{AC}\cong \overline{CE}, \overline{BC}\cong \overline{CD}\) | 2.Definition of a midpoint |
| 3. \(\Delta ACB\cong \Delta ECD\) | 3.SSS Postulate |
Note that you must clearly state the three sets of sides are congruent BEFORE stating the triangles are congruent.
Example \(\PageIndex{5}\)
The only way we will show two triangles are congruent in an \(x−y\) plane is using SSS.
Find the lengths of all the line segments from both triangles to see if the two triangles are congruent.
Solution
To do this, you need to use the distance formula.
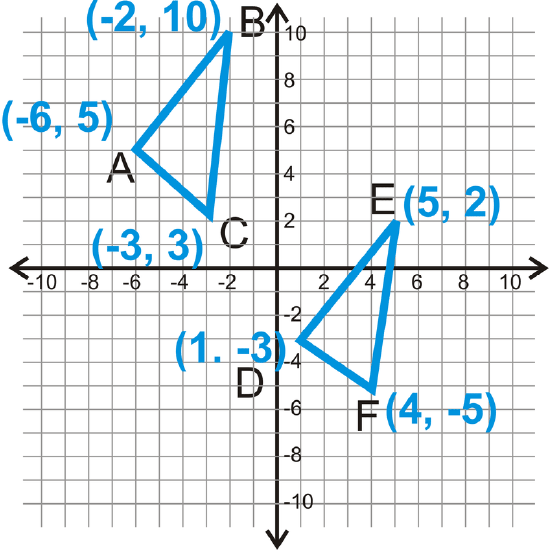
Begin with \(\Delta ABC\) and its sides.
\(\begin{align*} AB&=\sqrt{(−6−(−2))^2+(5−10)^2}\\ &=(−4)^2+(−5)^2\\ &=\sqrt{16+25}\\ &=\sqrt{41} \\ BC&=\sqrt{(−2−(−3))^2+(10−3)^2}\\ &=(1)^2+(7)^2\\ &=\sqrt{1+49}\\ &=\sqrt{50}\\ &=\sqrt{52} \\ AC&=\sqrt{(−6−(−3))^2+(5−3)^2}\\ &=\sqrt{(−3)^2+(2)^2}\\ &=\sqrt{9+4}\\ &=\sqrt{13} \end{align*}\)
Now, find the lengths of all the sides in \(\Delta DEF\).
\(\begin{align*} DE&=\sqrt{(1−5)^2+(−3−2)^2}\\ &=\sqrt{(−4)^2+(−5)^2}\\ &=\sqrt{16+25}\\ &=\sqrt{41} \\ EF&=\sqrt{(5−4)^2+(2−(−5))^2}\\ &=\sqrt{(1)^2+(7)^2}\\ &=\sqrt{1+49}\\ &=\sqrt{50}\\ &=5\sqrt{2}\\ DF&=\sqrt{(1−4)^2+(−3−(−5))^2}\\ &=\sqrt{(−3)^2+(2)^2}\\ &=\sqrt{9+4}\\ &=\sqrt{13} \end{align*}\)
\(AB=DE\), \(BC=EF\), and \(AC=DF\), so the two triangles are congruent by SSS.
Review
Are the pairs of triangles congruent? If so, write the congruence statement and why.
-
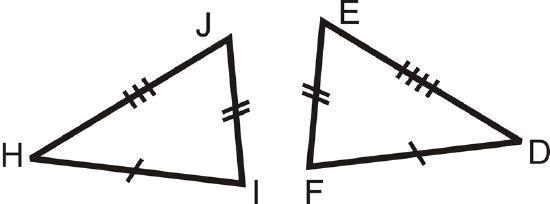
Figure \(\PageIndex{8}\) -
Figure \(\PageIndex{9}\) -
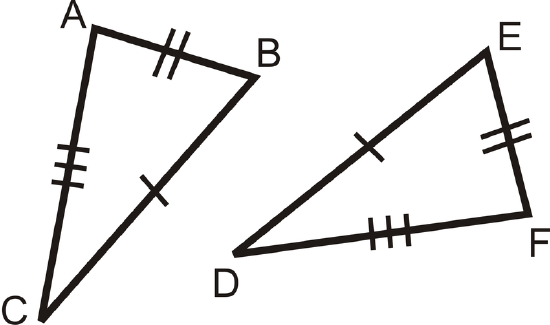
Figure \(\PageIndex{10}\) -
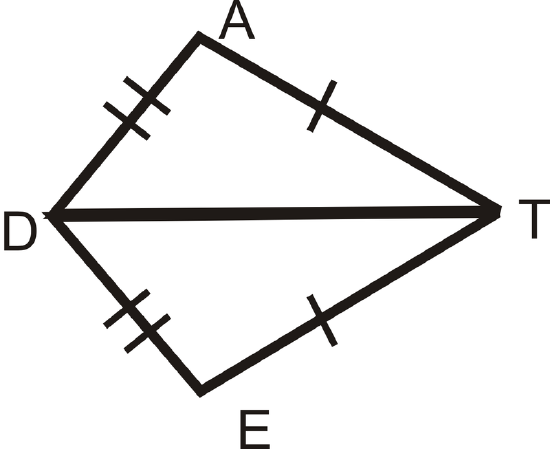Figure \(\PageIndex{11}\)
State the additional piece of information needed to show that each pair of triangles is congruent.
- Use SSS
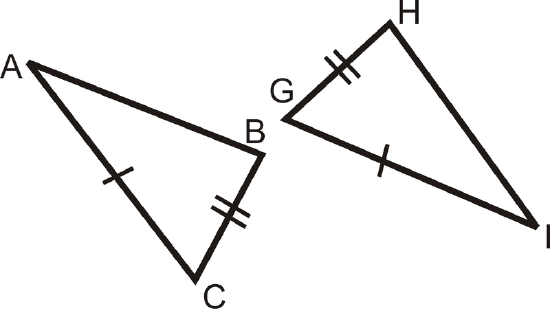Figure \(\PageIndex{12}\) - Use SSS
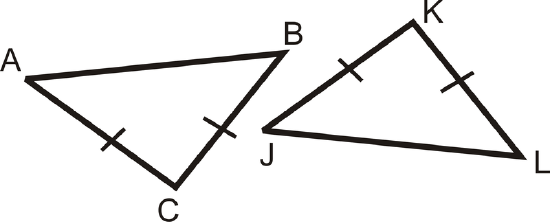Figure \(\PageIndex{13}\)
Fill in the blanks in the proofs below.
- Given: B is the midpoint of \(\overline{DC} \overline{AD}\cong \overline{AC}\) Prove: \(\Delta ABD\cong \Delta ABC \)
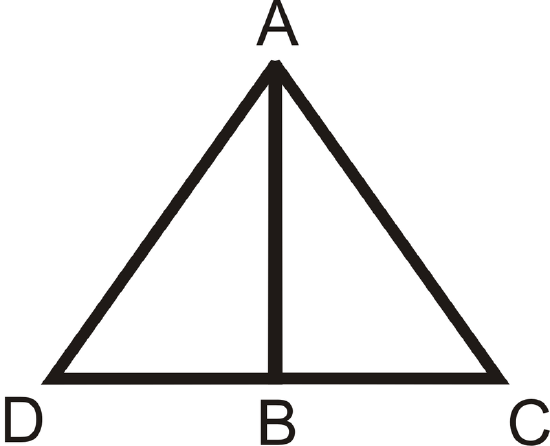
Figure \(\PageIndex{14}\)
| Statement | Reason |
|---|---|
| 1. | 1. |
| 2. | 2. Definition of a Midpoint |
| 3. | 3. Reflexive \(PoC\) |
| 4. \(\Delta ABD\cong \Delta ABC\) | 4. |
Find the lengths of the sides of each triangle to see if the two triangles are congruent. Leave your answers under the radical.
-
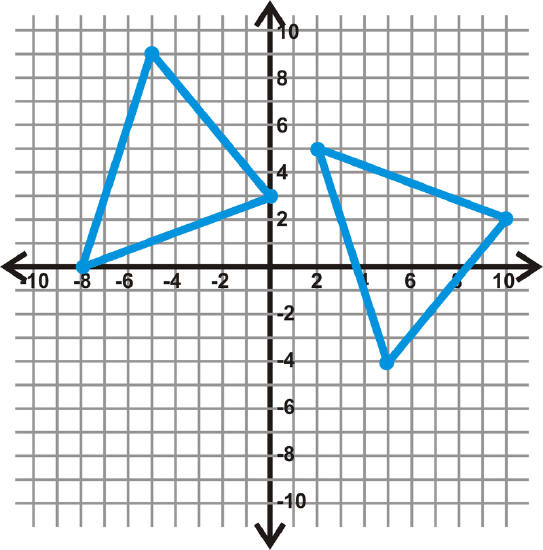
Figure \(\PageIndex{15}\) -
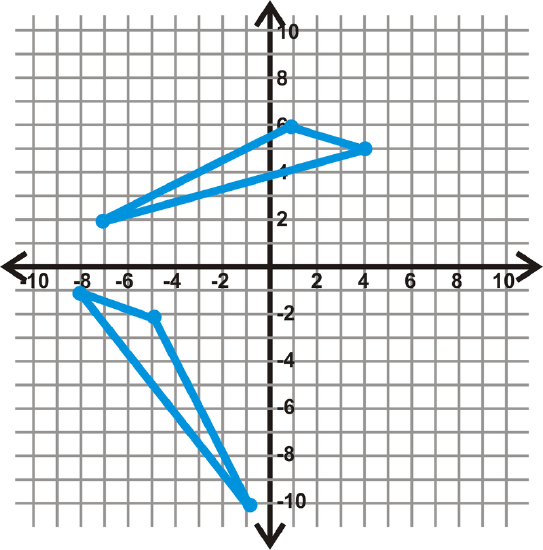
Figure \(\PageIndex{16}\) - \(\Delta ABC: A(−1,5), B(−4,2), C(2,−2)\) and \(\Delta DEF: D(7,−5), E(4,2), F(8,−9)\)
- \(\Delta ABC: A(−8,−3), B(−2,−4), C(−5,−9)\) and \(\Delta DEF: D(−7,2), E(−1,3), F(−4,8)\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.6.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Congruent | Congruent figures are identical in size, shape and measure. |
| Distance Formula | The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) can be defined as \(d=(x_2−x_1)^2+(y_2−y_1)^2\). |
| H-L (Hypotenuse-Leg) Congruence Theorem | If the hypotenuse and leg in one right triangle are congruent to the hypotenuse and leg in another right triangle, then the two triangles are congruent. |
| Side Side Side Triangle | A side side side triangle is a triangle where the lengths of all three sides are known quantities. |
| SSS | SSS means side, side, side and refers to the fact that all three sides of a triangle are known in a problem. |
| Triangle Congruence | Triangle congruence occurs if 3 sides in one triangle are congruent to 3 sides in another triangle. |
| Rigid Transformation | A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure. |
Additional Resources
Interactive Element
Video: Introduction to Congruent Triangles
Activities: SSS Triangle Congruence Discussion Questions
Study Aids: Triangle Congruence Study Guide
Practice: SSS
Real World: SSS Triangle Congruence