1.8: Identification of Angles by Vertex and Ray
- Page ID
- 2135
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learn how to name angles using letters.
 Figure \(\PageIndex{1}\)
Figure \(\PageIndex{1}\)Donyell walks from his house to his school. Then, after school he walks to his friend's house. He notices that his journey forms an angle. He decides to name the angle. Donyell labels his house as point \(H\), his school as point S and his friend's house as point \(F\). Can you use the points to name of the angle formed by his journey?
In this concept, you will learn about the parts of an angle.
Identifying Angles by Vertex and Ray
An angle is one of the key geometric figures that you will be working with in geometry. An angle is created when two rays connect at a common point.
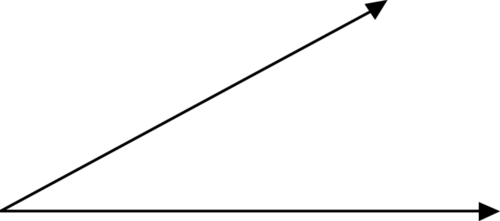 Figure \(\PageIndex{2}\)
Figure \(\PageIndex{2}\)You can see that the two rays are connected at a common endpoint, called a vertex. This forms the angle. An angle is named by points on the rays.
Let's look at an example of an angle.
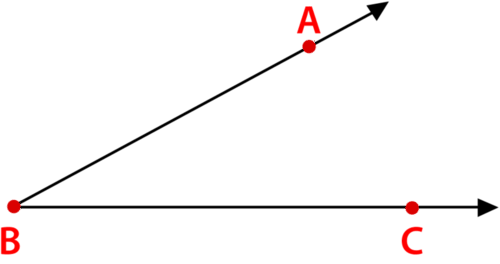 Figure \(\PageIndex{3}\)
Figure \(\PageIndex{3}\)This is angle \(ABC\). The vertex \(B\) is always in the middle. The symbol for angle looks like a small angle.
\(\angle ABC\)
Angle \(ABC\) is named with this symbol.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Donyell and his walk to school and then to his friend's house.
Name the angle if his house is point \(H\), his school is point \(S\) and his friend's house is point \(F\).
Solution
First, determine the common endpoint.
\(S\)
Then, name the angle.
\(\angle HSF\)
The answer is \(\angle HSF\).
Example \(\PageIndex{2}\)
What is the common endpoint of the rays that form \(\angle HIJ\)?
Solution
First, determine the name of the common endpoint.
The vertex
Next, identify the location of the vertex in the angle name.
The middle point
Then, write the point.
\(I\)
The answer is \(I\). The common endpoint of the rays that form \(\angle HIJ\) is \(I\).
Example \(\PageIndex{3}\)
Name this angle. Be sure that the vertex is in the middle.
 Figure \(\PageIndex{4}\)
Figure \(\PageIndex{4}\)Solution
First, locate the common endpoint.
\(E\)
Then, name the angle.
\(\angle DEF\)
The answer is \(\angle DEF\).
Example \(\PageIndex{4}\)
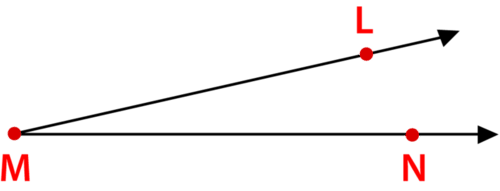 Figure \(\PageIndex{5}\)
Figure \(\PageIndex{5}\)Solution
First, locate the common endpoint.
\(M\)
Then, name the angle.
\(\angle LMN\)
The answer is \(\angle LMN\)
Example \(\PageIndex{5}\)
What is the common endpoint of the rays that form \(\angle QRS\)?
Solution
First, determine the name of the common endpoint.
The vertex
Next, identify the location of the vertex in the angle name.
The middle point
Then, write the point.
\(R\)
The answer is \(R\). The common endpoint of the rays that form \(\angle QRS\) is \(R\).
Review
Draw a picture to illustrate each of the named geometric figures.
- \(\overrightarrow{AB}\)
- \(\overleftrightarrow{CD}\)
- \(\overleftrightarrow{DE}\)
- \(\angle ABC\)
- \(\angle LMN\)
- \(\overline{XY}\)
- \(\overrightarrow{PQ}\)
- \(\overleftrightarrow{GH}\)
- \(\overleftrightarrow{AB} \parallel \overleftrightarrow{DE}\)
- \(\overleftrightarrow{LM} \parallel \overleftrightarrow{DE}\)
- \(\overleftrightarrow{RS} \parallel \overleftrightarrow{TU}\)
- \(\overline{DF} \parallel \overline{XY}\)
Define the following terms.
- Ray
- Line
- Vertex
- Line Segment
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.3.
Vocabulary
| Term | Definition |
|---|---|
| Angle | A geometric figure formed by two rays that connect at a single point or vertex. |
| Intersecting lines | Intersecting lines are lines that cross or meet at some point. |
| line | A line is a straight one-dimensional figure that extends forever in opposite directions. |
| line segment | A line segment is a part of a line that has two endpoints. |
| Parallel | Two or more lines are parallel when they lie in the same plane and never intersect. These lines will always have the same slope. |
| Point | A point is a location in space that does not have size or shape. |
| Point of Intersection | A point of intersection is the point where two intersecting lines meet. |
| Ray | A ray is a part of a line that has one endpoint and continues indefinitely in one direction. |
| Vertex | A vertex is a point of intersection of the lines or rays that form an angle. |
Additional Resource
Interactive Element
Video: Introduction to Angles
Practice: Identification of Angles by Vertex and Ray

