1.7: Introduction to Angles
- Page ID
- 2133
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Comparison and classification of angles, such as right or vertical, and their relation to lines and rays.
Line Segment and Ray
A line segment is a portion of a line with two endpoints. A ray is a portion of a line with one endpoint. Line segments are named by their endpoints and rays are named by their endpoint and another point. In each case, a segment or ray symbol is written above the points. Below, the line segment is \(\overline{AB}\) and the ray is \(\overrightarrow{AB}\).
Angles
- When two rays meet at their endpoints, they form an angle.
- Depending on the situation, an angle can be named with an angle symbol \(\angle\) and its vertex, or by three letters.
If three letters are used, the middle letter should be the vertex. The angle below could be called \(\angle B\) or \(\angle ABC\) or \(\angle CBA\). Use three letters to name an angle if using one letter would not make it clear what angle you are talking about.
The size of an angle is measured in degrees. Therefore, 'the measure of the angle ABC' refers to the size, or measure, of the angle in degrees, often written \(m \angle ABC\). You can use a protractor or geometry software to measure angles. Remember that a full circle has \(360 ^{\circ}\).
Types of Angles
- An angle that is exactly \(0 ^{\circ}\) is called a zero angle.
- An angle that is less than \(90 ^{\circ}\) is called an acute angle.
- An angle that is exactly \(90 ^{\circ}\) (one quarter of a circle) is called a right angle. A right angle is noted with a little square at its vertex.
- An angle that is more than 90∘but less than \(180 ^{\circ}\) is called an obtuse angle. An angle that is exactly \(180 ^{\circ}\) (one half of a circle) is called a straight angle.
Identifying the Type of Angles
Name the angle below and classify it by its measure.
\(m \angle F\) or \(m \angle DFE\) or \(m \angle EFD\). It is _____ angle.
Interactive Element
Add interactive element text here. This box will NOT print up in pdfs
Interactive Element
Complementary and Supplementary Angles
Two angles are complementary if the sum of their measures is \(90 ^{\circ}\).
Two angles are supplementary if the sum of their measures is \(180 ^{\circ}\).
Two angles that together form a straight angle will always be supplementary.
Finding an Unknown Angle
\(x\) and \(y\) are complementary angles with measure of \(y= 20^{\circ}\). What is the measure of \(x\)?
The measure of \(x\) is _____.
Adjacent and Vertical Angles
When two lines intersect, many angles are formed, as shown below.
In the diagram above, \(\angle AEC\) and \(\angle AED\) are adjacent angles because they are next to each other and share a ray. They are also supplementary, because together they form a straight angle. \(\angle AEC\) and \(\angle DEB\) are called vertical angles. Vertical angles will always have the same measure.
Consider this example problem:
Let \(m \angle AEC=x^{\circ}\). Show that \(m \angle DEB\) must also equal \(x^{\circ}\).
This shows that vertical angles will always have the same measure.
Identifying Angles
Explain why you must use three letters to identify any of the angles in the diagram below.
All angles in this diagram have a vertex of E. Therefore ∠E is ambiguous because it could refer to many different angles. Use three letters with E as the middle letter to be clear about which angle you are referring to \(\angle AEC\), \(\angle AED\), \(\angle DEB\), \(\angle BEC\).
Example \(\PageIndex{1}\)
Angles are formed by intersecting lines or rays. If you take any two lines or rays, will you form at least one angle?
Solution
As long as the lines or rays intersect, at least one angle will be formed. If the lines (or rays) are parallel, and therefore don't intersect, then no angles will be formed.
Example \(\PageIndex{2}\)
Estimate the measure of angle \(\angle DFE\). Use a protractor to confirm your answer.
Solution
Remember that exactly half of a right angle is \(45^{\circ}\). This angle looks to be more than half of a right angle. You might guess that it is approximately \(55^{\circ}\). Using a protractor, you can see that it is about \(60^{\circ}\).
Example \(\PageIndex{3}\)
What are two lines that form a right angle called?
Solution
Perpendicular lines.
Interactive Element
Review
1. What's the difference between a line segment, a line, and a ray?
2. Draw an example of a right angle.
3. Draw an example of an obtuse angle.
4. Draw an example of an acute angle.
5. Why are two angles that make a straight angle always supplementary?
6. If \(m\angle ABC= (2x+4)^{\circ}\), \(m\angle DEF= (3x−5)^{\circ}\), and \(\angle ABC\) and \(\angle DEF\) are complementary, what are the measures of the angles?
7. If \(m\angle ABC= (2x+4)^{\circ}\), \(m\angle DEF= (3x−5)^{\circ}\), and \(\angle ABC\) and \(\angle DEF\) are supplementary, what are the measures of the angles?
Use the diagram below for #8-#12.
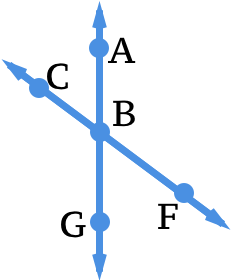Figure \(\PageIndex{12}\)8. Give an example of vertical angles.
9. Give an example of a straight angle.
10. Give an example of supplementary angles.
11. If \(m\angle ABC= 70^{\circ}\), find \(m\angle ABF\).
12. If \(m\angle ABC= 70^{\circ}\), find \(m\angle FBG\).
13. What do you remember about perpendicular lines?
Use the angle in the image for #14-#15.
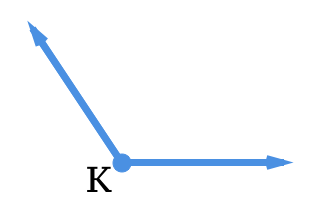Figure \(\PageIndex{13}\)14. Name the angle and classify it based on its size.
15. Estimate the measure of the angle. Use a protractor to confirm your answer.
16. Draw a diagram in which two angles are supplementary to the same angle. What must be true about the original two angles? Explain.
17. We use the term complementary to describe angles that sum to ___ and supplementary to describe angles that sum to ___. What about angles that sum to \(360^{\circ}\)? Invent a name for such angles and justify your choice.
18. Draw two vertical angles. How much must each ray of one of the vertical angles be rotated in order to match up with the other vertical angle? Explain.
19. Draw two angles of the same measure that are not vertical. Draw two angles that are supplementary but not adjacent. Draw two angles that are adjacent and have the same measure. What is the measure of each angle in the last drawing? Why?
Review (Answers)
To see the Review answers, click here.