1.4: Midpoints and Segment Bisector
- Page ID
- 2120
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Use midpoints and bisectors to find the halfway mark between two coordinates.
When two segments are congruent, we indicate that they are congruent, or of equal length, with segment markings, as shown below:
Figure \(\PageIndex{1}\)A midpoint is a point on a line segment that divides it into two congruent segments.
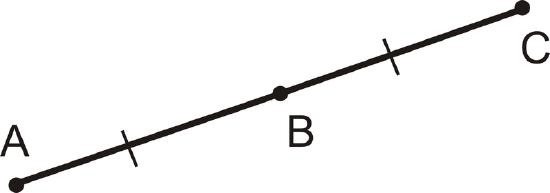Figure \(\PageIndex{2}\)Because \(AB=BC\), \(B\) is the midpoint of \(\overline{AC}\). Any line segment will have exactly one midpoint.
When points are plotted in the coordinate plane, we can use a formula to find the midpoint between them.
Here are two points, \((-5, 6)\) and \((3, 2).\)
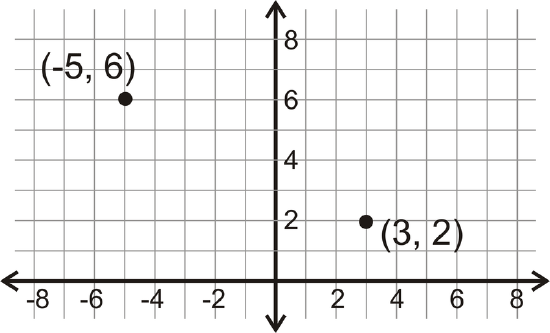Figure \(\PageIndex{3}\)The midpoint should be halfway between the points on the segment connecting them. Just by looking, it seems like the midpoint is \((-1, 4).\)
Midpoint Formula: For two points, (\(x_1, y_1\)) and (\(x_2,y_2\)), the midpoint is \(\left (\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right) \).
Let’s use the formula to make sure \((-1, 4)\) is the midpoint between \((-5, 6)\) and \((3, 2)\).
\(\left (\dfrac{-5+3}{2} ,\dfrac{6+2}{2}\right) =(−22,82)=(−1,4) \)
A segment bisector cuts a line segment into two congruent parts and passes through the midpoint. A perpendicular bisector is a segment bisector that intersects the segment at a right angle.
\(\overline{AB} \cong \overline{BC}\)
\(\overline{AC} \perp \overleftrightarrow{DE}\)
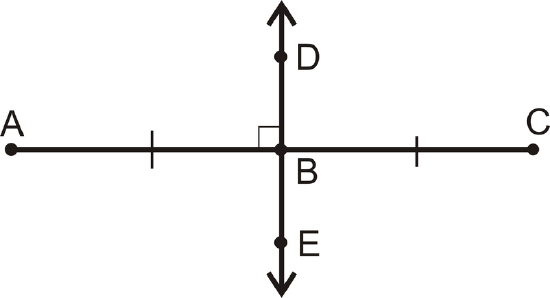Figure \(\PageIndex{4}\)What if you were given the coordinates of two points and you wanted to find the point exactly in the middle of them? How would you find the coordinates of this third point?
Example \(\PageIndex{1}\)
Write all equal segment statements.
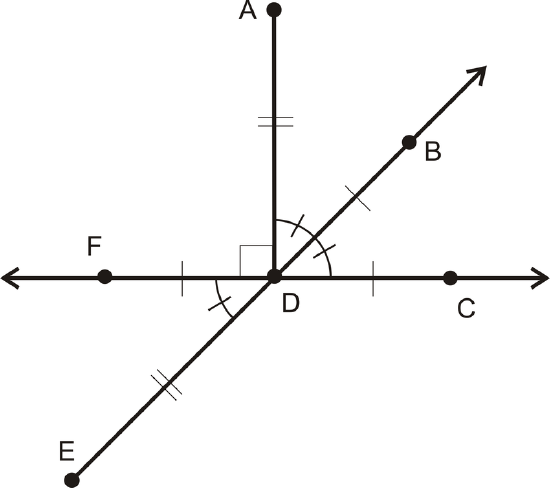Figure \(\PageIndex{5}\)Solution
\(AD=DE\)
\(FD=DB=DC\)
Example \(\PageIndex{2}\)
Is \(M\) a midpoint of \(\overline{AB}\)?
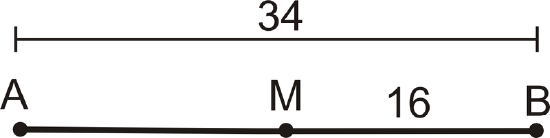
Solution
No, it is not \(MB=16\) and \(AM=34−16=18\). \(AM\) must equal \(MB\) in order for M to be the midpoint of \(\overline{AB}\).
Example \(\PageIndex{3}\)
Find the midpoint between \((9, -2)\) and \((-5, 14)\).
Solution
Plug the points into the formula.
\(\left(\dfrac{9+(−5)}{2}\ ,\dfrac{−2+14}{2}\right)=\left(\dfrac{4}{2},\dfrac{12}{2}\right)=(2,6)\)
Example \(\PageIndex{4}\)
Which line is the perpendicular bisector of \(\overline{MN}\)?
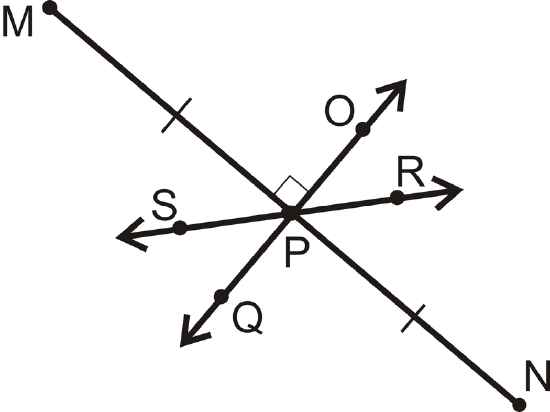Figure \(\PageIndex{7}\)Solution
The perpendicular bisector must bisect \(\overline{MN}\) and be perpendicular to it. Only \(\overleftrightarrow{OQ}\) fits this description. \(\overleftrightarrow{SR}\) is a bisector, but is not perpendicular.
Example \(\PageIndex{5}\)
Find \(x\) and \(y\).
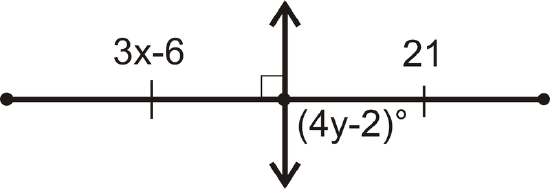Figure \(\PageIndex{8}\)Solution
The line shown is the perpendicular bisector.
So, \(3x−6=21\)
\(3x=27\)
\(x=9\)
And, \((4y−2)=90\)
\(4y=92\)
\(y=23\)
Review
- Copy the figure below and label it with the following information:
\(\overline{AB} \cong \overline{AD}\)
\(\overline{CD} \cong \overline{BC}\)
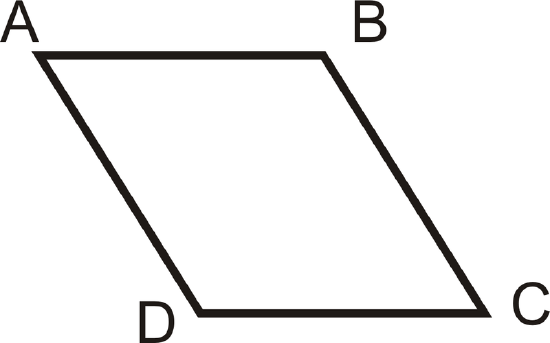Figure \(\PageIndex{9}\)For 2-4, use the following picture to answer the questions.
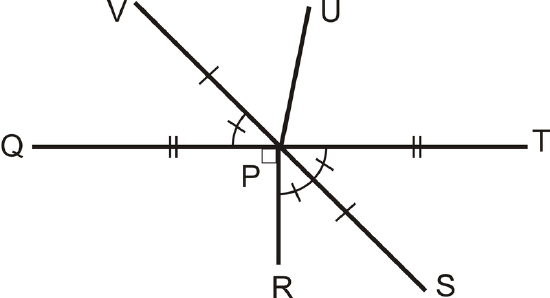Figure \(\PageIndex{10}\)- \(P\) is the midpoint of what two segments?
- How does \(\overline{VS}\) relate to \(\overline{QT}\)?
- How does \(\overline{QT}\) relate to \(\overline{VS}\)?
For exercise 5, use algebra to determine the value of \(x\).
-
Figure \(\PageIndex{11}\)
For questions 6-10, find the midpoint between each pair of points.
- (-2, -3) and (8, -7)
- (9, -1) and (-6, -11)
- (-4, 10) and (14, 0)
- (0, -5) and (-9, 9)
- (-3, -5) and (2, 1)
Given the midpoint (\(M\)) and either endpoint of \(\overline{AB}\), find the other endpoint.
- \(A(−1,2)\) and \(M(3,6)\)
- \(B(−10,−7)\) and \(M(−2,1)\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.4.
Vocabulary
| Term | Definition |
|---|---|
| midpoint | The midpoint of a line segment is the point on the line segment that splits the segment into two congruent parts. |
| perpendicular bisector | A segment bisector that intersects the segment at a right angle. |
| segment bisector | A segment bisector is a line (or part of a line) that passes through the midpoint. |
| segment markings | When two segments are congruent, we indicate that they are congruent with segment markings. |
| Midpoint Formula | The midpoint formula says that for endpoints \((x_1, y_1)\) and \((x_2, y_2)\), the midpoint is \( \left (\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)\). |
Additional Resources
Interactive Element
Video: Midpoints and Segment Bisectors Examples - Basic
Activities: Midpoints and Segment Bisectors Discussion Questions
Study Aids: Segments Study Guide
Practice: Midpoints and Segment Bisectors
Real World: Midpoint And Segment Bisectors - Treasure Hunt Activity