2.1: Basic Visual Patterns

Describe non-arithmetic sequences by finding a rule. Identify visual and geometric patterns

Figure \(\PageIndex{1}\)

Whitney is on a school trip to Italy. The fifth day there her group visits Venice where she gets to see the Doge's Palace. She notices a visual pattern in the architecture and snapped the photo above. How could Whitney describe this visual pattern? What type of visual pattern is it?

In this concept, you will learn to recognize, describe, and extend visual patterns.

Visual Patterns

A visual pattern is a sequence of pictures or geometric objects that have been created based on some rule. There are two categories of visual patterns that you will learn about here.

1. Some visual patterns are made up of a sequence of pictures or geometric objects that repeat over and over. These types of patterns are called repeating patterns. The sequence of pictures that repeat is called the pattern unit.
2. Some visual patterns are based on a picture or geometric object that keeps increasing or decreasing in size in a specific way. These types of patterns have a pattern rule that help to describe how the picture or object is growing or shrinking.

Here is an example of a visual pattern that is a repeating pattern.

Find the pattern unit for the pattern below.

Figure \(\PageIndex{2}\)

First, notice that this visual pattern is made up of circles, squares, and triangles.

Next, look carefully to see how the shapes have been placed. After each circle is a square, after each square is two triangles, and after each pair of triangles is another circle. This is a repeating pattern because the same set of four pictures repeats over and over.

The pattern unit for this visual pattern is the set of pictures that repeats.

The answer is that the pattern unit is "circle, square, triangle, triangle":

Figure \(\PageIndex{3}\)

Once you understand the pattern and know the pattern unit, you can extend the pattern. The next picture in our sequence of pictures would be a triangle.

Here is an example of an increasing visual pattern.

Find a pattern rule to describe the pattern below. What will the next step in the pattern look like?

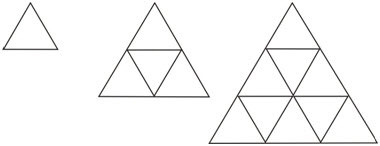Figure \(\PageIndex{4}\)

As you can see, this pattern is different from a repeating pattern because the geometric objects keep getting bigger and bigger. There is not a pattern unit that repeats, but you can find a pattern rule to describe what is happening.

To find the pattern rule, look to see how the steps in the pattern are related. Each new big triangle is made up of more and more smaller triangles. In fact, each new big triangle is made up of the previous big triangle plus an additional row of small triangles.

• The first step in the pattern has just one row of 1 triangle.
• The second step in the pattern has two rows of 1 triangle, then 3 triangles.
• The third step in the pattern has three rows of 1 triangle, then 3 triangles, then 5 triangles.

You can see that the number of rows of triangles corresponds to the step in the pattern. Each time a new row is added, it has 2 more triangles than the row above it.

The answer for the pattern rule is: to get the next step in the pattern, take the previous step and add another row of small triangles to the bottom with 2 more triangles than the row above it.

Now that you have the pattern rule, you can extend the pattern.

You'd expect the next step in the pattern to look like the third step in the pattern except with an additional row of triangles.

The answer is that the fourth step in the pattern will have four rows of 1 triangle, then 3 triangles, then 5 triangles, then 7 triangles:

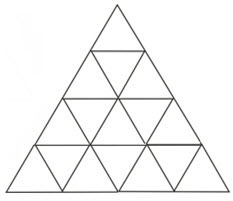Figure \(\PageIndex{5}\)

Example \(\PageIndex{1}\)

Earlier, you were given a problem about Whitney and her school trip to Italy.

She got to see the Doge's Palace in Venice where she noticed an interesting visual pattern in the architecture.

Solution

First, notice that this is a repeating pattern. Objects are being repeated as opposed to increasing/decreasing in size.

As this is a repeating pattern, next try to describe the pattern unit.

The same column with railing is being repeated over and over. This is the pattern unit.

The answer is that this is a repeating pattern with a pattern unit that is a column/railing pair.

Example \(\PageIndex{2}\)

What will the next step in the pattern below look like?

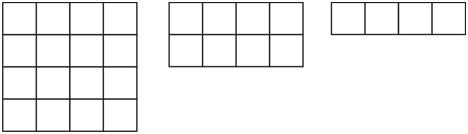Figure \(\PageIndex{6}\)

Solution

First, notice that this is a decreasing visual pattern.

To find the pattern rule, look to see how the steps in the pattern are related. Each new rectangle is made up of fewer and fewer squares. In fact, each new rectangle is made up of half as many squares as the previous rectangle.

• The first step in the pattern has 16 squares.
• The second step in the pattern has 8 squares.
• The third step in the pattern has 4 squares.

You can see that if you take the number of squares in one step of the pattern and divide by 2, you will get the number of squares in the next step of the pattern.

The answer is that the pattern rule is to get the number of squares in the next step in the pattern, take the number of squares in the previous step and divide by 2.

Now that you have the pattern rule, you can extend the pattern.

You'd expect the next step in the pattern to have half as many squares as the third step. The third step has 4 squares, so the fourth step will have two squares.

The answer is that the next step in the pattern will look like:

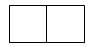Figure \(\PageIndex{7}\)

Example \(\PageIndex{3}\)

Describe the following pattern. What is its pattern unit or pattern rule?

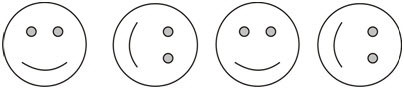Figure \(\PageIndex{8}\)

Solution

First notice that this is a repeating pattern. Images are being repeated as opposed to increasing/decreasing in size.

Next, look carefully to see how the images have been placed. After each smiley face with the mouth on the bottom is a smiley face with the mouth on the left. The same set of two pictures repeats over and over.

The answer is that this is a repeating pattern. The pattern unit is:

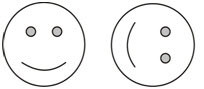Figure \(\PageIndex{9}\)

Example \(\PageIndex{4}\)

Describe the following pattern. What is its pattern unit or pattern rule?

Figure \(\PageIndex{10}\)

Solution

First notice that this is a repeating pattern. Images are being repeated as opposed to increasing/decreasing in size.

Next, look carefully to see how the images have been placed. After each set of lines is an arrow. The same set of two pictures repeats over and over.

The answer is that this is a repeating pattern. The pattern unit is:

Figure \(\PageIndex{11}\)

Example \(\PageIndex{5}\)

Continue the described pattern with the next two shapes.

Triangle, star, triangle, star, square, square, triangle, star, triangle

Solution

First notice that this is a repeating pattern. The images haven't been displayed, but they have been described. The images are being repeated as opposed to increasing/decreasing in size.

Next, look carefully to see how the shapes have been ordered. After "triangle, star, triangle, star" is "square, square". After "square, square" the "triangle, star, ..." sequence seems to repeat. It appears that the same set of six shapes will repeat over and over.

The pattern unit is "triangle, star, triangle, star, square, square".

Now that you have the pattern unit, you can extend the pattern. After the "triangle, star, triangle" at the end of the pattern will be another star, then two squares, and then back to the beginning of the pattern unit with "triangle, star, triangle, star, square, square...".

The answer is that the next two shapes will be "star, square".

Review

Write a rule for each number pattern.

1. \(4,7,13,25\)
2. \(216,196,176,156\)
3. \(1,7,19,43\)
4. \(10,000, 1,000, 100, 10\)

Write the next number in each pattern.

5. \(4,7,13,25,_____\)
6. \(216,196,176,156, _____\)
7. \(1, 7, 19, 43,_____\)
8. \(10,000, 1,000, 100, 10, _____\)

Write down the next image in each pattern based on the description.

9. A hexagon, a pentagon, a square, _____
10. Five dots, ten dots, fifteen dots, _____
11. Fifteen dots, fourteen dots, twelve dots, _____
12. Two triangles, four triangles, three triangles, six triangles, five triangles, _____
13. An octagon, a hexagon, an octagon, a pentagon, an octagon, ____
14. One square, 1.5 squares, 2 squares, 2.5 squares, _____
15. Eighteen circles, nine circles, four and a half circles _____

Review (Answers)

To see the Review answers, open this PDF file and look for section 1.3.

Additional Resources

Interactive Element

Video: Geometric Sequences (Introduction)

Practice: Basic Visual Patterns

Real World: The Math Behind It All