3.4: Corresponding Angles
- Page ID
- 2190
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify corresponding angles as matching angles.
Corresponding angles are two angles that are in the "same place" with respect to the transversal but on different lines. Imagine sliding the four angles formed with line \(l\) down to line \(m\). The angles which match up are corresponding.
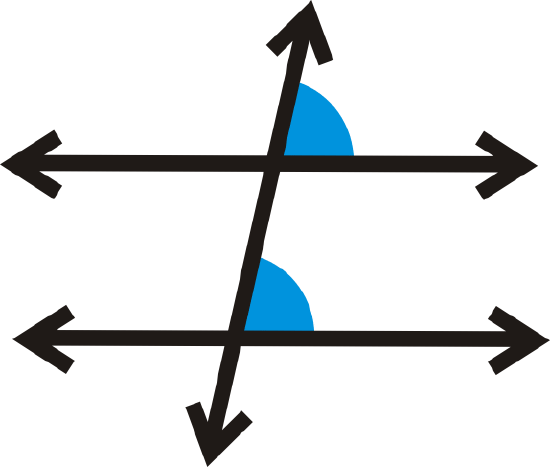
Corresponding Angles Postulate: If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
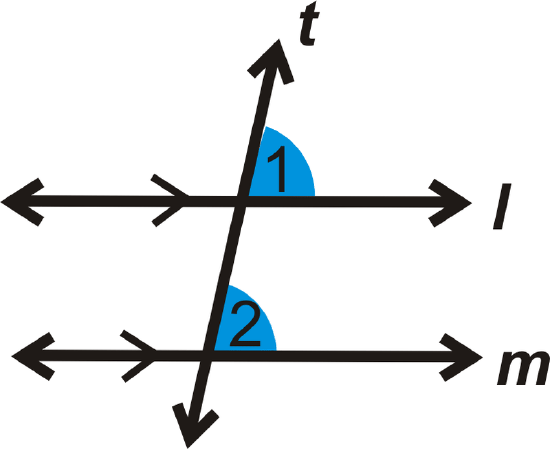
If \(l \parallel m\), then \(\angle 1\cong \angle 2\).
Converse of Corresponding Angles Postulate: If corresponding angles are congruent when two lines are cut by a transversal, then the lines are parallel.
If
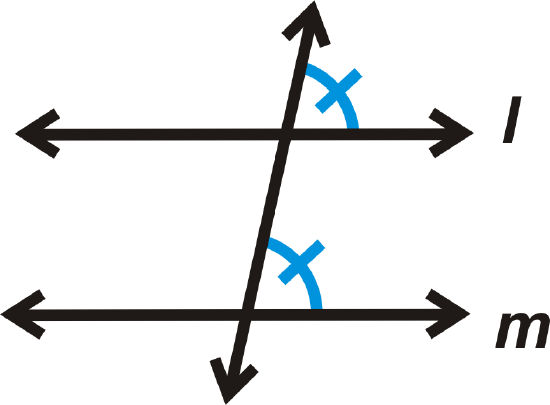
then \(l \parallel m\).
What if you were presented with two angles that are in the same place with respect to the transversal but on different lines? How would you describe these angles and what could you conclude about their measures?
Example \(\PageIndex{1}\)
If \(m\angle 2=76^{\circ}\), what is \(m\angle 6\)?

Solution
\(\angle 2\) and \(\angle 6\) are corresponding angles and l||m from the arrows in the figure. \(\angle 2\cong \angle 6\) by the Corresponding Angles Postulate, which means that \(m\angle 6=76^{\circ}\).
Example \(\PageIndex{2}\)
Using the measures of \angle 2 and \angle 6 from Example 1, find all the other angle measures.
Solution
If \(m\angle 2=76^{\circ}\), then \(m\angle 1=180^{\circ}−76^{\circ}=104^{\circ}\) (linear pair). \angle 3\cong \angle 2 \)(vertical angles), so \(m\angle 3=76^{\circ}\). \(m\angle 4=104^{\circ}\) (vertical angle with \angle 1\)).
By the Corresponding Angles Postulate, we know \(\angle 1\cong \angle 5\), \(\angle 2\cong \angle 6\), \(\angle 3\cong \angle 7\), and \(\angle 4\cong \angle 8\), so \(m\angle 5=104^{\circ}\), \(m\angle 6=76^{\circ}\), \(m\angle 7=76^{\circ}\), and \(m\angle 8=104^{\circ}\).
Example \(\PageIndex{3}\)
Find the value of y:
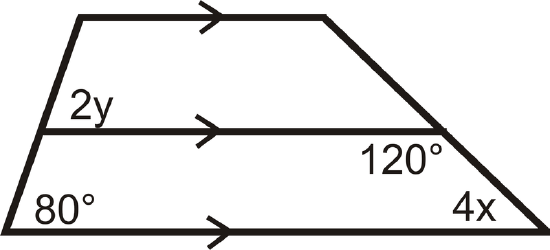
Solution
The horizontal lines are marked parallel and the angle marked \(2y\) is corresponding to the angle marked 80 so these two angles are congruent. This means that \(2y=80\) and therefore \(y=40\).
Example \(\PageIndex{4}\)
If a||b, which pairs of angles are congruent by the Corresponding Angles Postulate?
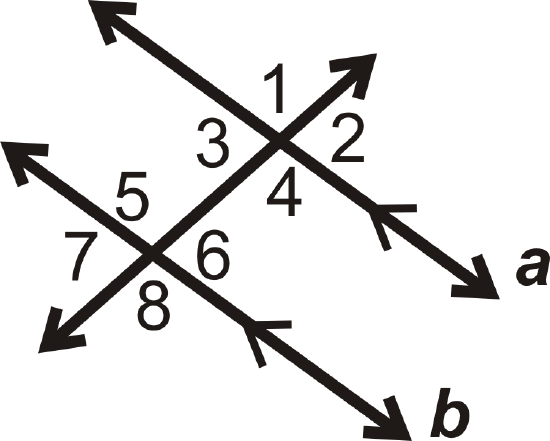
Solution
There are 4 pairs of congruent corresponding angles:
\(\angle 1\cong \angle 5\), \(\angle 2\cong \angle 6\), \(\angle 3\cong \angle 7\), and \(\angle 4\cong \angle 8\).
Example \(\PageIndex{5}\)
If \(m\angle 8=110^{\circ}\) and \(m\angle 4=110^{\circ}\), then what do we know about lines \(l\) and \(m\)?

Solution
\(\angle 8\) and \(\angle 4\) are corresponding angles. Since \(m\angle 8=m\angle 4\), we can conclude that l||m.
Review
- Determine if the angle pair \(\angle 4\) and \(\angle 2\) is congruent, supplementary or neither:
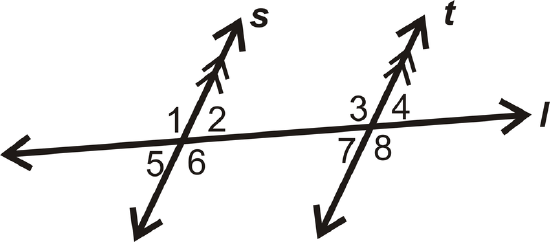
Figure \(\PageIndex{8}\) - Give two examples of corresponding angles in the diagram:
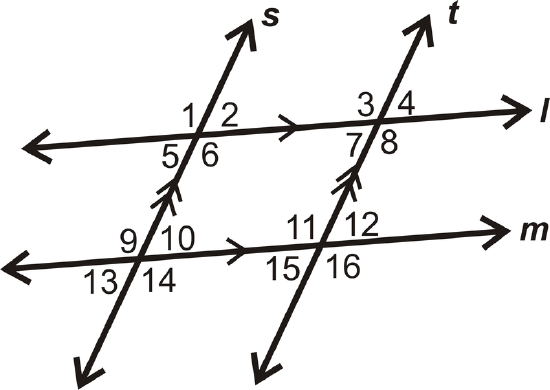
Figure \(\PageIndex{9}\) - Find the value of \(x\):
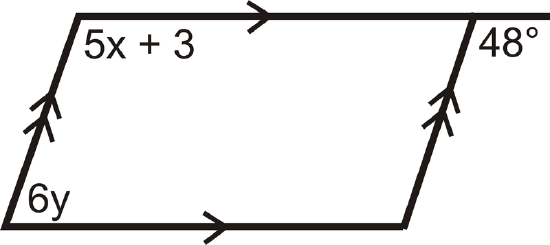
Figure \(\PageIndex{10}\) - Are the lines parallel? Why or why not?
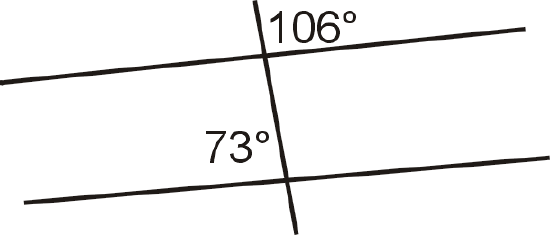
Figure \(\PageIndex{11}\) - Are the lines parallel? Justify your answer.
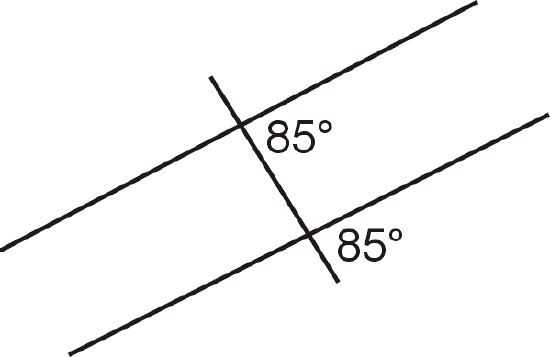
Figure \(\PageIndex{12}\)
For 6-10, what does the value of \(x\) have to be to make the lines parallel?
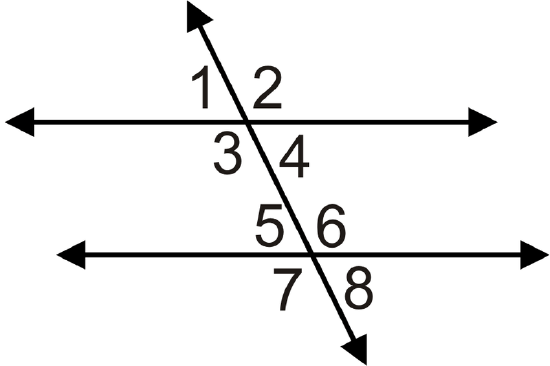
- If \(m\angle 1=(6x−5)^{\circ}\) and \(m\angle 5=(5x+7)^{\circ}\).
- If \(m\angle 2=(3x−4)^{\circ}\) and \(m\angle 6=(4x−10)^{\circ}\).
- If \(m\angle 3=(7x−5)^{\circ}\) and \(m\angle 7=(5x+11)^{\circ}\).
- If \(m\angle 4=(5x−5)^{\circ}\) and \(m\angle 8=(3x+15)^{\circ}\).
- If \(m\angle 2=(2x+4)^{\circ}\) and \(m\angle 6=(5x−2)^{\circ}\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 3.3.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Corresponding Angles | Corresponding angles are two angles that are in the same position with respect to the transversal, but on different lines. |
Additional Resource
Interactive Element
Video: Corresponding Angles Principles - Basic
Activities: Corresponding Angles Discussion Questions
Study Aids: Angles and Transversals Study Guide
Practice: Corresponding Angles
Real World: Corresponding Angles

