4.36: Distance and Triangle Classification Using the Pythagorean Theorem

Find missing sides to calculate the area.

Applications of the Pythagorean Theorem

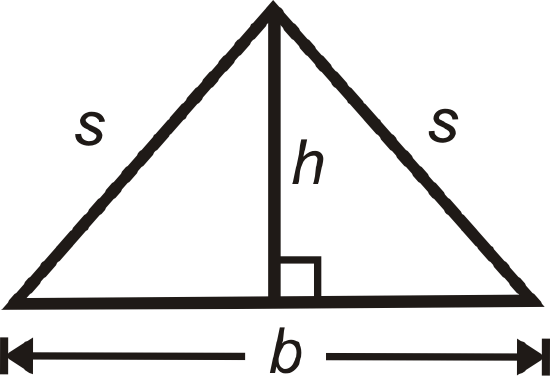
Find the Height of an Isosceles Triangle

One way to use The Pythagorean Theorem is to find the height of an isosceles triangle (see Example 1).

Figure \(\PageIndex{1}\)

Prove the Distance Formula

Another application of the Pythagorean Theorem is the Distance Formula. We will prove it here.

Figure \(\PageIndex{2}\)

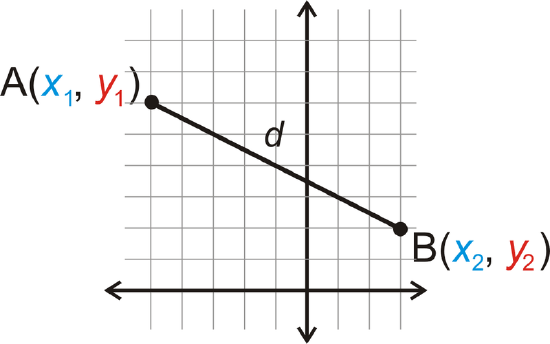
Let’s start with point \(A(x_1,y_1)\) and point \(B(x_2, y_2)\). We will call the distance between \(A\) and \(B\), \(d\).

Draw the vertical and horizontal lengths to make a right triangle.

Figure \(\PageIndex{3}\)

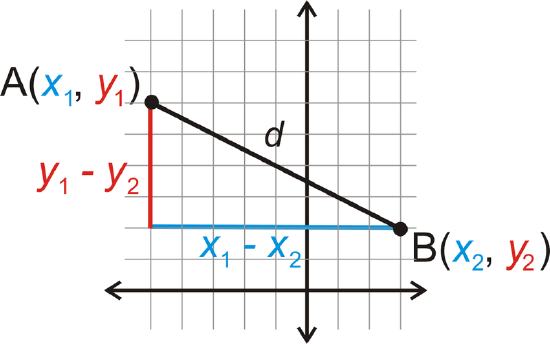
Now that we have a right triangle, we can use the Pythagorean Theorem to find the hypotenuse, \(d\).

\(\begin{align*} d^2=(x_1−x_2)^2+(y_1−y_2)^2 \\ d=\sqrt{(x_1−x_2)^2+(y_1−y_2)^2} \end{align*} \)

Distance Formula: The distance between \(A(x_1, y_1)\) and \(B(x_2, y_2)\) is \(d=\sqrt{(x_1−x_2)^2+(y_1−y_2)^2}\).

Classify a Triangle as Acute, Right, or Obtuse

We can extend the converse of the Pythagorean Theorem to determine if a triangle is an obtuse or acute triangle.

Acute Triangles: If the sum of the squares of the two shorter sides in a right triangle is greater than the square of the longest side, then the triangle is acute.

Figure \(\PageIndex{4}\)

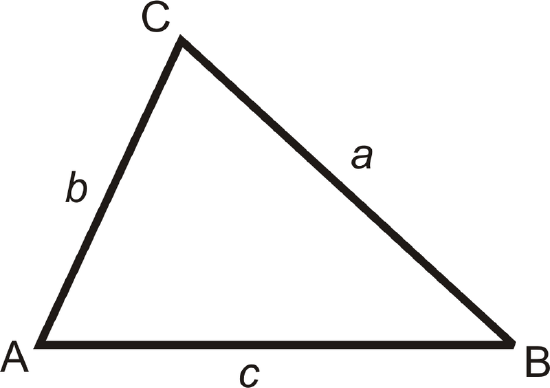
For \(b<c\) and \(a<c\), if \(a^2+b^2>c^2\), then the triangle is acute.

Obtuse Triangles: If the sum of the squares of the two shorter sides in a right triangle is less than the square of the longest side, then the triangle is obtuse.

Figure \(\PageIndex{5}\)

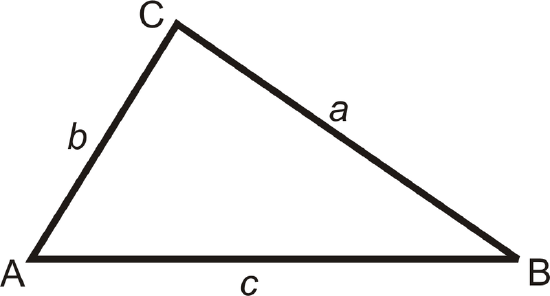
For \(b<c\) and \(a<c\), if \(a^2+b^2<c^2\), then the triangle is obtuse.

What if you were given an equilateral triangle in which all the sides measured 4 inches? How could you use the Pythagorean Theorem to find the triangle's altitude?

Example \(\PageIndex{1}\)

What is the height of the isosceles triangle?

Figure \(\PageIndex{6}\)

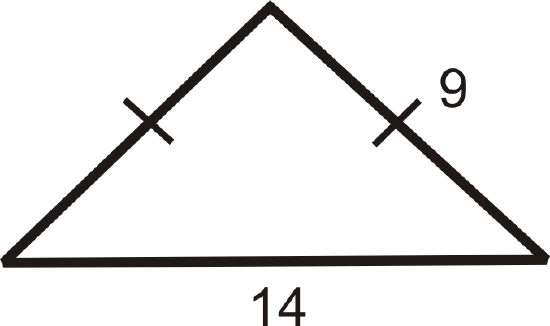
Solution

Draw the altitude from the vertex between the congruent sides, which will bisect the base.

Figure \(\PageIndex{7}\)

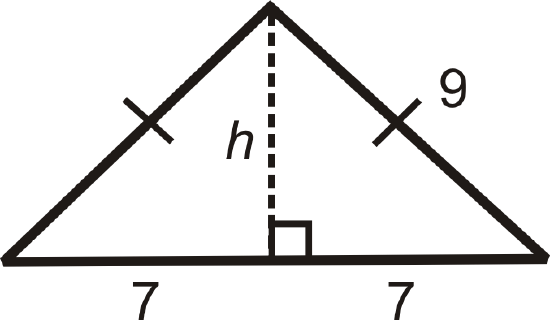
\(\begin{align*} 7^2+h^2&=9^2 \\ 49+h^2&=81 \\ h^2&=32 \\ h&=\sqrt{32}=\sqrt{16\cdot 2}=4\sqrt{2}\end{align*}\)

Example \(\PageIndex{2}\)

Find the distance between \((1, 5)\) and \((5, 2)\).

Solution

Make \(A(1,5)\) and \(B(5,2)\). Plug into the distance formula.

\(\begin{align*} d &=\sqrt{(1−5)^2+(5−2)^2} \\ &=\sqrt{(−4)^2+(3)^2} \\ &=\sqrt{16+9}=\sqrt{25}=5\end{align*}\)

Just like the lengths of the sides of a triangle, distances are always positive.

Example \(\PageIndex{3}\)

Graph \(A(−4,1)\), \(B(3,8)\), and \(C(9,6)\). Determine if \(\Delta{ABC}\) is acute, obtuse, or right.

Figure \(\PageIndex{8}\)

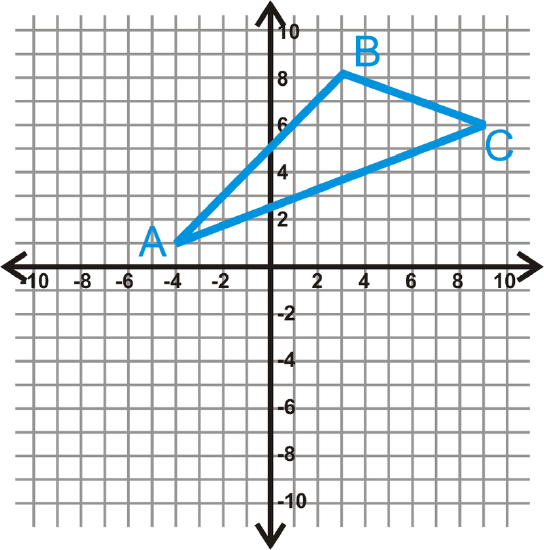
Solution

Use the distance formula to find the length of each side.

\(\begin{align*} AB&=\sqrt{(−4−3)^2+(1−8)^2}=\sqrt{49+49}=\sqrt{98} \\ BC &=\sqrt{(3−9)^2+(8−6)^2}=\sqrt{36+4}=\sqrt{40} \\ AC &=\sqrt{(−4−9)^2+(1−6)^2}=\sqrt{169+25}=\sqrt{194}\end{align*}\)

Plug these lengths into the Pythagorean Theorem.

\(\begin{align*} \sqrt{98})^2+(\sqrt{40})^2 &? (\sqrt{194})^2 \\ 98+40 &? 194 \\ 138 &< 194\end{align*}\)

\(\Delta{ABC}\) is an obtuse triangle.

For Examples 4 and 5, determine if the triangles are acute, right or obtuse.

Example \(\PageIndex{4}\)

Set the longest side to c.

Figure \(\PageIndex{9}\)

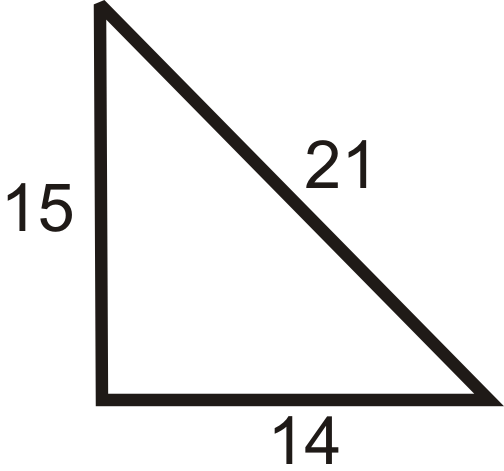
Solution

\(\begin{align*} 15^2+14^2 &? \: 21^2 \\ 225+196 &? \: 441 \\ 421 &< 441\end{align*}\)

The triangle is obtuse.

Example \(\PageIndex{5}\)

Set the longest side to \(c\).

Solution

A triangle with side lengths 5, 12, 13.

\(5^2+12^2=13^2\) so this triangle is right.

Review

Find the height of each isosceles triangle below. Simplify all radicals.

1. 

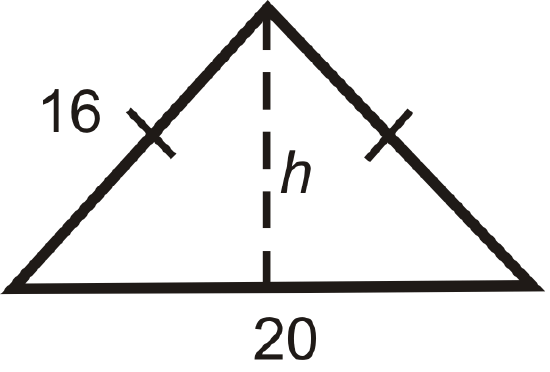
   Figure \(\PageIndex{10}\)

2. 

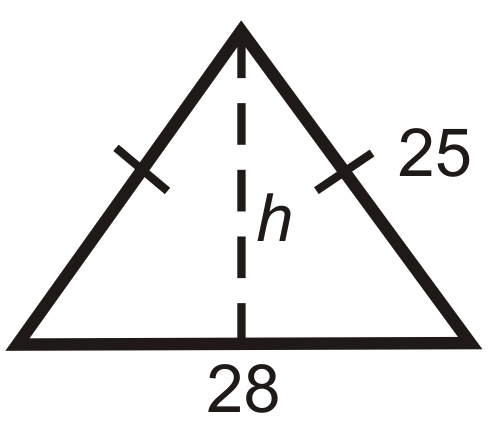
   Figure \(\PageIndex{11}\)

3. 

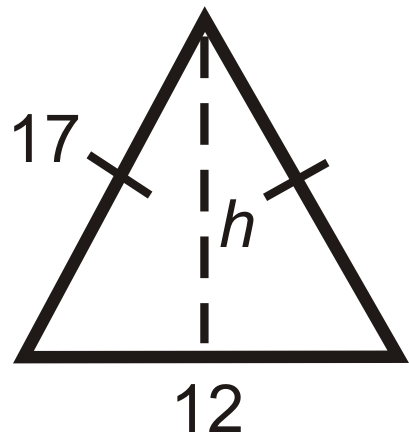
   Figure \(\PageIndex{12}\)

Find the length between each pair of points.

4. \((-1, 6)\) and \((7, 2)\)
5. \((10, -3)\) and \((-12, -6)\)
6. \((1, 3)\) and \((-8, 16)\)
7. What are the length and width of a 42” HDTV? Round your answer to the nearest tenth.
8. Standard definition TVs have a length and width ratio of 4:3. What are the length and width of a 42” Standard definition TV? Round your answer to the nearest tenth.

Determine whether the following triangles are acute, right or obtuse.

9. 7, 8, 9
10. 14, 48, 50
11. 5, 12, 15
12. 13, 84, 85
13. 20, 20, 24
14. 35, 40, 51
15. 39, 80, 89
16. 20, 21, 38
17. 48, 55, 76

Graph each set of points and determine whether \Delta{ABC} is acute, right, or obtuse, using the distance formula.

18. \(A(3,−5), B(−5,−8), C(−2,7)\)
19. \(A(5,3), B(2,−7), C(−1,5)\)
20. \(A(1,6), B(5,2), C(−2,3)\)
21. \(A(−6,1), B(−4,−5), C(5,−2)\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 8.3.

Resources

Vocabulary

Term	Definition
acute triangle	A triangle where all angles are less than 90∘.
Obtuse Triangle	An obtuse triangle is a triangle with one angle that is greater than 90 degrees.
Distance Formula	The distance between two points \((x_1,y_1)\) and \((x_2, y_2)\) can be defined as \(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\).
Pythagorean Theorem	The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle, given by \(a^2+b^2=c^2\), where a and b are legs of the triangle and c is the hypotenuse of the triangle.
Vertex	A vertex is a point of intersection of the lines or rays that form an angle.

Additional Resources

Interactive Element

Video: The Pythagorean Theorem and The Converse of the Pythagorean Theorem

Activities: Applications of the Pythagorean Theorem Discussion Questions

Practice: Distance and Triangle Classification Using the Pythagorean Theorem