4.42: 45-45-90 Right Triangles
- Page ID
- 4983
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Leg times \(\sqrt{2}\) equals hypotenuse.
A right triangle with congruent legs and acute angles is an Isosceles Right Triangle. This triangle is also called a 45-45-90 triangle (named after the angle measures).
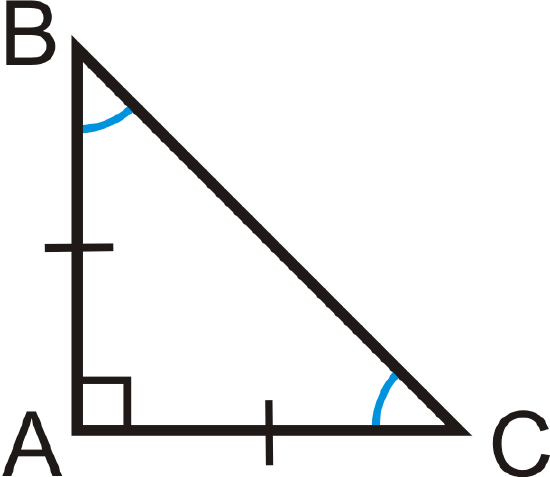
\(\Delta ABC\) is a right triangle with \(m\angle A=90^{\circ}\), \(\overline{AB}\cong \overline{AC}\) and \(m\angle B=m\angle C=45^{\circ}\).
45-45-90 Theorem: If a right triangle is isosceles, then its sides are in the ratio \(x:x:x\sqrt{2}\). For any isosceles right triangle, the legs are x and the hypotenuse is always \(x\sqrt{2}\).
What if you were given an isosceles right triangle and the length of one of its sides? How could you figure out the lengths of its other sides?
Example \(\PageIndex{1}\)
Find the length of \(x\).
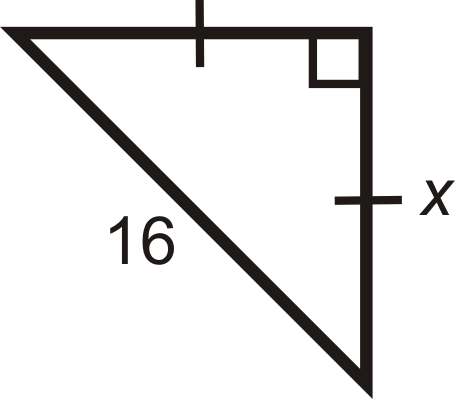
Solution
Use the \(x:x:x\sqrt{2}\) ratio.
Here, we are given the hypotenuse. Solve for \(x\) in the ratio.
\(\begin{aligned} x\sqrt{2}&=16 \\ x&=\dfrac{16}{\sqrt{2}}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{16\sqrt{2}}{2}=8\sqrt{2}\end{aligned}\)
Example \(\PageIndex{2}\)
Find the length of \(x\), where \(x\) is the hypotenuse of a 45-45-90 triangle with leg lengths of \(5\sqrt{3}\).
Solution
Use the \(x:x:x\sqrt{2}\) ratio.
\(x=5\sqrt{3}\cdot \sqrt{2}=5\sqrt{6}\)
Example \(\PageIndex{3}\)
Find the length of the missing side.
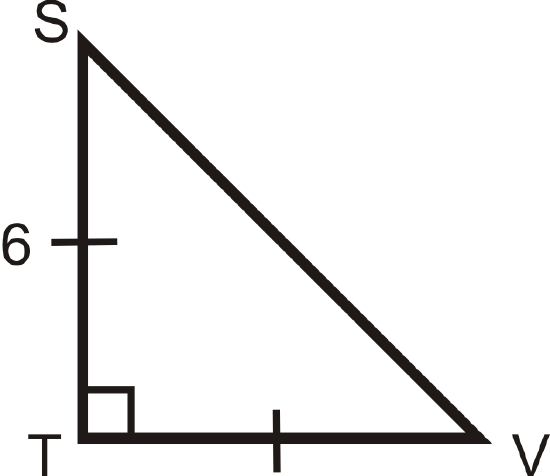
Solution
Use the \(x:x:x\sqrt{2}\) ratio. \(TV=6\) because it is equal to \(ST\). So, \(SV=6\cdot \sqrt{2}=6\sqrt{2}\).
Example \(\PageIndex{4}\)
Find the length of the missing side.
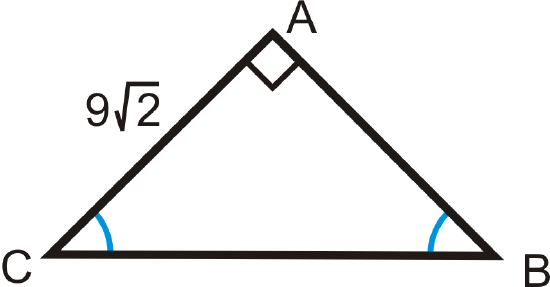
Solution
Use the \(x:x:x\sqrt{2}\) ratio. \(AB=9\sqrt{2}\) because it is equal to \(AC\). So, \(BC=9\sqrt{2}\cdot \sqrt{2}=9\cdot 2=18\).
Example \(\PageIndex{5}\)
A square has a diagonal with length 10, what are the lengths of the sides?
Solution
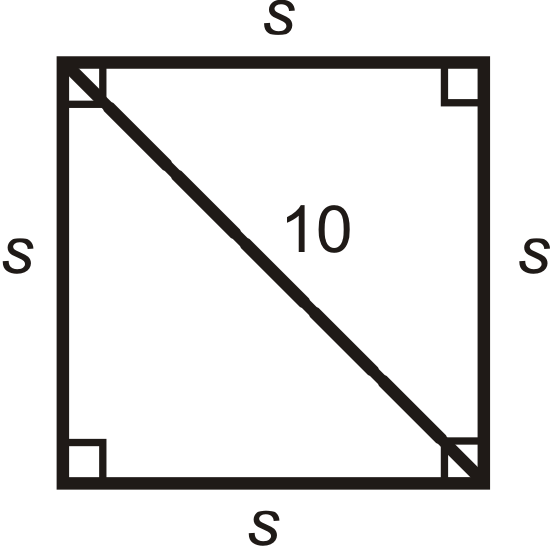
We know half of a square is a 45-45-90 triangle, so \(10=s\sqrt{2}\).
\(\begin{aligned} s\sqrt{2}&=10 \\ s&=10\sqrt{2}\cdot \sqrt{2}\sqrt{2}=10\sqrt{2}2=5\sqrt{2}\end{aligned}\)
Review
- In an isosceles right triangle, if a leg is 4, then the hypotenuse is __________.
- In an isosceles right triangle, if a leg is \(x\), then the hypotenuse is __________.
- A square has sides of length 15. What is the length of the diagonal?
- A square’s diagonal is 22. What is the length of each side?
For questions 5-11, find the lengths of the missing sides. Simplify all radicals.
-
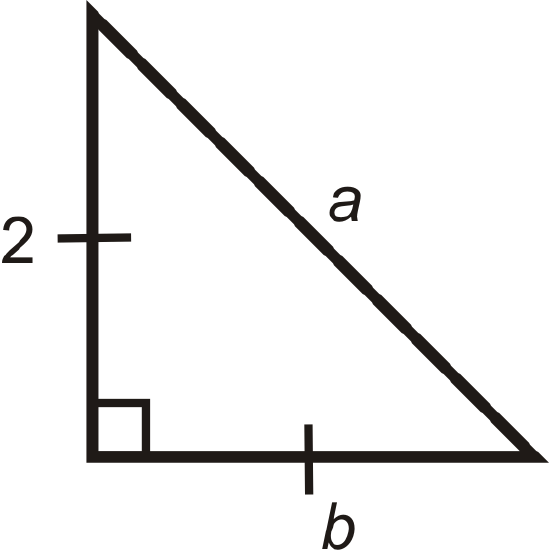
Figure \(\PageIndex{6}\) -
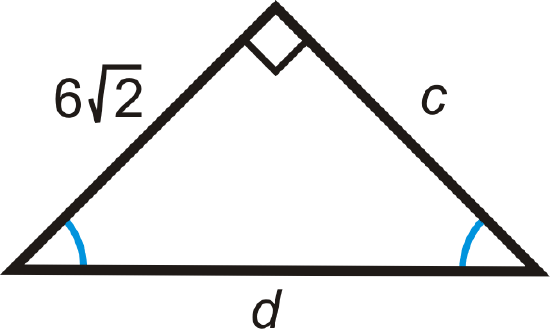
Figure \(\PageIndex{7}\) -
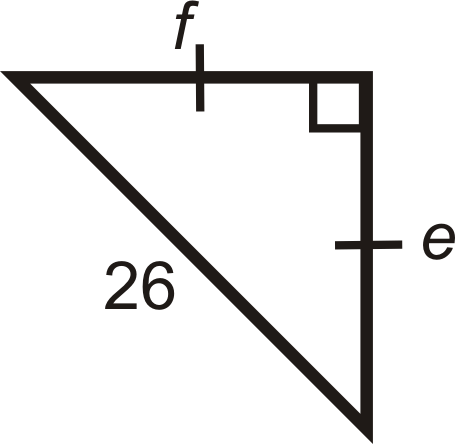
Figure \(\PageIndex{8}\) -
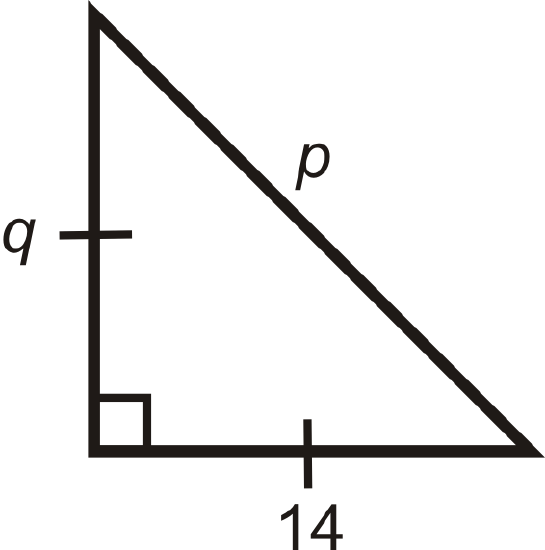
Figure \(\PageIndex{9}\) -
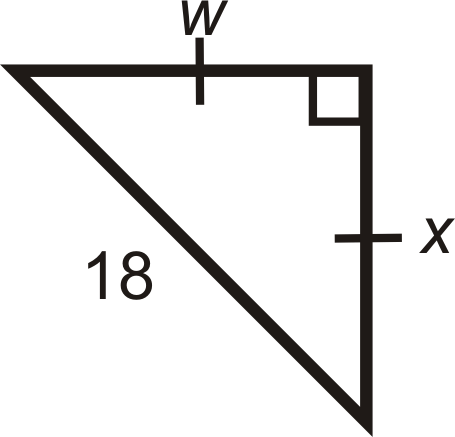
Figure \(\PageIndex{10}\) -
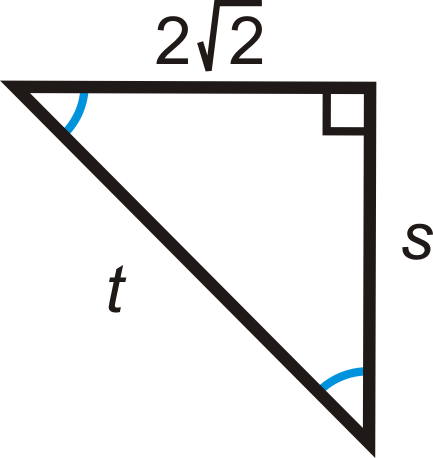
Figure \(\PageIndex{11}\) -
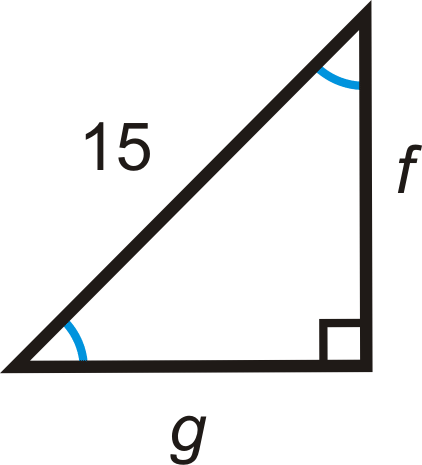
Figure \(\PageIndex{12}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.5.
Resources
Vocabulary
| Term | Definition |
|---|---|
| 45-45-90 Theorem | For any isosceles right triangle, if the legs are x units long, the hypotenuse is always \(x\sqrt{2}\). |
| 45-45-90 Triangle | A 45-45-90 triangle is a special right triangle with angles of \(45^{\circ}\), \(45^{\circ}\), and \(90^{\circ}\). |
| Hypotenuse | The hypotenuse of a right triangle is the longest side of the right triangle. It is across from the right angle. |
| Legs of a Right Triangle | The legs of a right triangle are the two shorter sides of the right triangle. Legs are adjacent to the right angle. |
| Radical | The \(\sqrt\), or square root, sign. |
Additional Resources
Interactive Element
Video: Solving Special Right Triangles
Activities: 45-45-90 Right Triangles Discussion Questions
Study Aids: Special Right Triangles Study Guide
Practice: 45-45-90 Right Triangles
Real World: Fighting the War on Drugs Using Geometry and Special Triangles