5.16: Kites
- Page ID
- 5000
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Quadrilaterals with two distinct sets of adjacent, congruent sides.
A kite is a quadrilateral with two distinct sets of adjacent congruent sides. It looks like a kite that flies in the air.

From the definition, a kite could be concave. If a kite is concave, it is called a dart. The word distinct in the definition means that the two pairs of congruent sides have to be different. This means that a square or a rhombus is not a kite.
The angles between the congruent sides are called vertex angles. The other angles are called non-vertex angles. If we draw the diagonal through the vertex angles, we would have two congruent triangles.
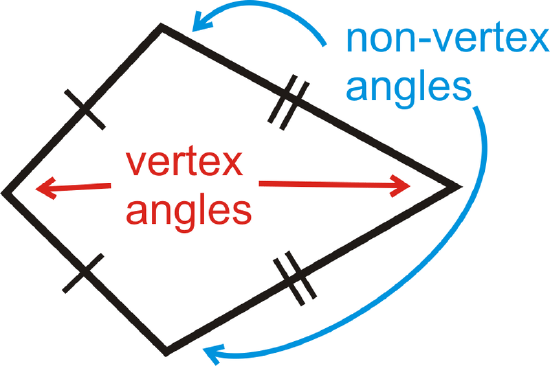
Facts about Kites
1. The non-vertex angles of a kite are congruent.
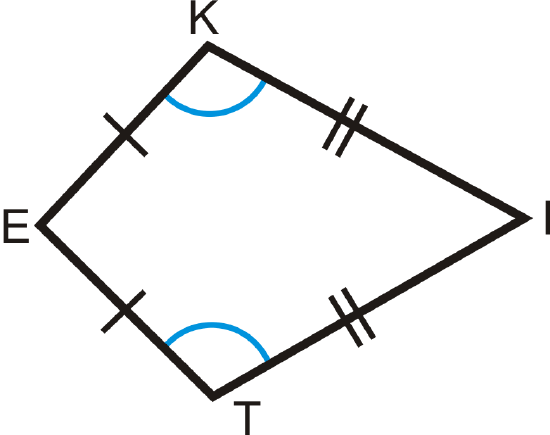
If \(KITE\) is a kite, then \(\angle K\cong \angle T\).
2. The diagonal through the vertex angles is the angle bisector for both angles.

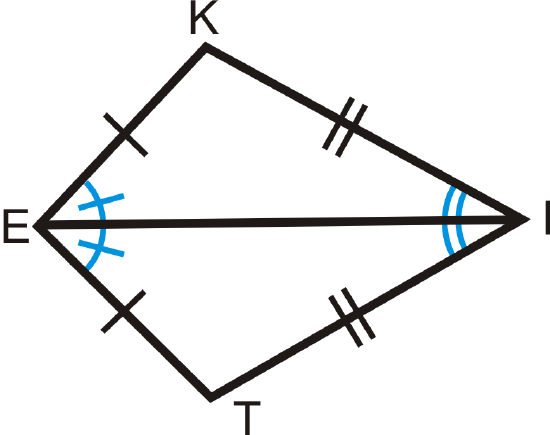 Figure \(\PageIndex{4}\)
Figure \(\PageIndex{4}\)If \(KITE\) is a kite, then \(\angle KEI\cong \angle IET\) and \(\angle KIE\cong \angle EIT\).
3. Kite Diagonals Theorem: The diagonals of a kite are perpendicular.
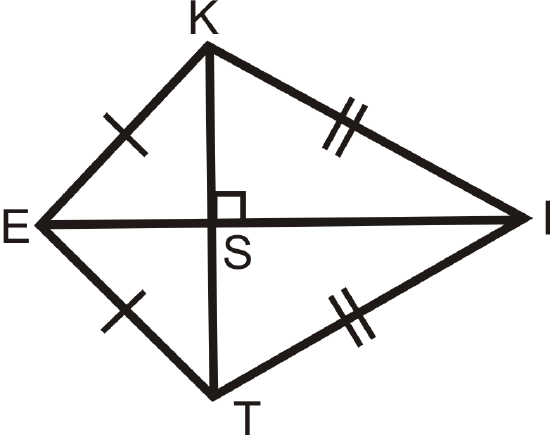 Figure \(\PageIndex{5}\)
Figure \(\PageIndex{5}\)\( \Delta KET\) and \(\Delta KIT\) are isosceles triangles, so \(\overline{EI}\) is the perpendicular bisector of \(\overline{KT}\) (Isosceles Triangle Theorem).
What if you were told that \(WIND\) is a kite and you are given information about some of its angles or its diagonals? How would you find the measure of its other angles or its sides?
For Examples 1 and 2, use the following information:
\(KITE\) is a kite.
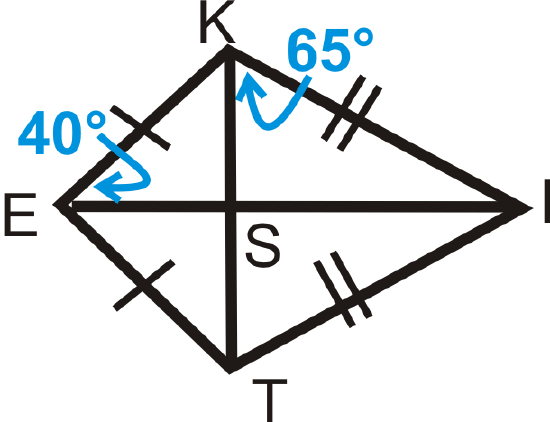
Example \(\PageIndex{1}\)
Find \(m\angle KIS\).
Solution
\(m\angle KIS=25^{\circ}\) by the Triangle Sum Theorem (remember that \angle KSI is a right angle because the diagonals are perpendicular.)
Example \(\PageIndex{2}\)
Find \(m\angle IST\).
Solution
\(m\angle IST=90^{\circ}\) because the diagonals are perpendicular.
Example \(\PageIndex{3}\)
Find the missing measures in the kites below.
-
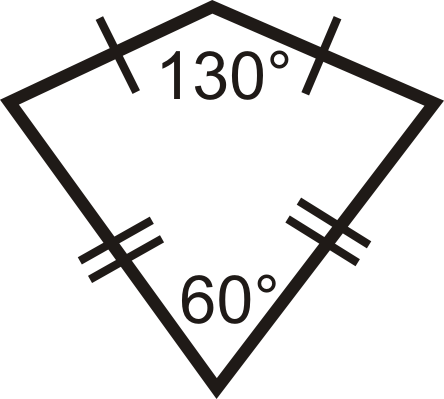
Figure \(\PageIndex{7}\) -
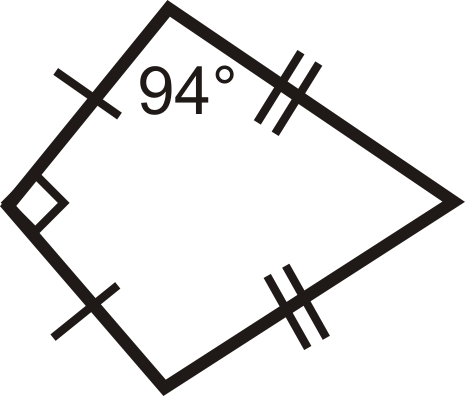
Figure \(\PageIndex{8}\)
Solution
- The two angles left are the non-vertex angles, which are congruent.
\( \begin{aligned} 130^{\circ} +60^{\circ} +x+x=360^{\circ} \\ 2x&=170^{\circ} \\ x&=85^{\circ} \qquad Both angles are 85^{\circ} \end{aligned}\)
- The other non-vertex angle is also \(94^{\circ}\). To find the fourth angle, subtract the other three angles from \(360^{\circ}\).
\(\begin{aligned} 90^{\circ} +94^{\circ} +94^{\circ} +x &=360^{\circ} \\ x&=82^{\circ} \end{aligned}\)
Example \(\PageIndex{4}\)
Use the Pythagorean Theorem to find the lengths of the sides of the kite.
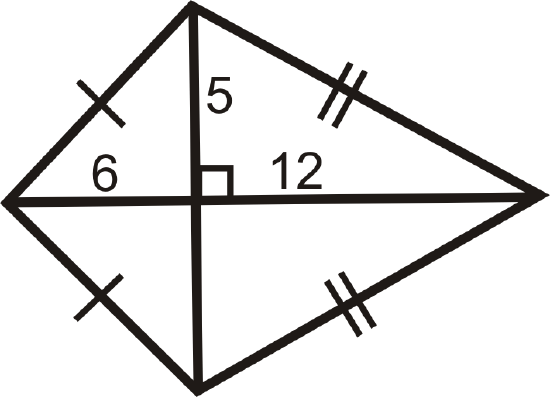
Solution
Recall that the Pythagorean Theorem says \(a^2+b^2=c^2\), where \(c\) is the hypotenuse. In this kite, the sides are the hypotenuses.
\(\begin{array}{rr}
6^{2}+5^{2}=h^{2} & 12^{2}+5^{2}=j^{2} \\
36+25=h^{2} & 144+25=j^{2} \\
61=h^{2} & 169=j^{2} \\
\sqrt{61}=h & 13=j
\end{array}\)
Example \(\PageIndex{5}\)
Prove that the non-vertex angles of a kite are congruent.
Given: \(KITE\) with \(\overline{KE}\cong \overline{TE}\) and \(\overline{KI}\cong \overline{TI}\)
Prove: \(\angle K\cong \angle T\)
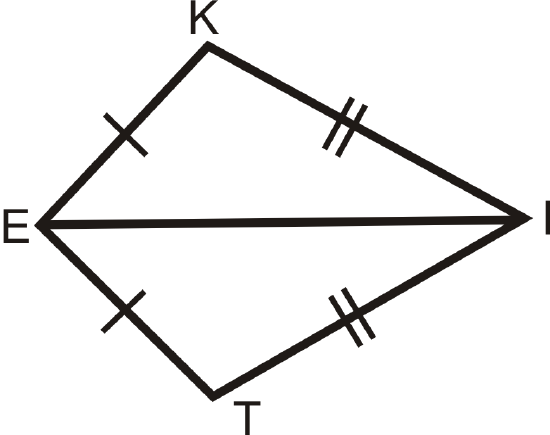
Solution
| Statement | Reason |
|---|---|
| 1. \(\overline{KE}\cong \overline{TE}\) and \(\overline{KI}\cong \overline{TI}\) | 1. Given |
| 2.\( \overline{EI}\cong \overline{EI}\) | 2. Reflexive PoC |
| 3. \(\Delta EKI\cong \Delta ETI\) | 3. SSS |
| 4. \(\angle K\cong \angle T\) | 4. CPCTC |
Review
For questions 1-6, find the value of the missing variable(s). All figures are kites.
-
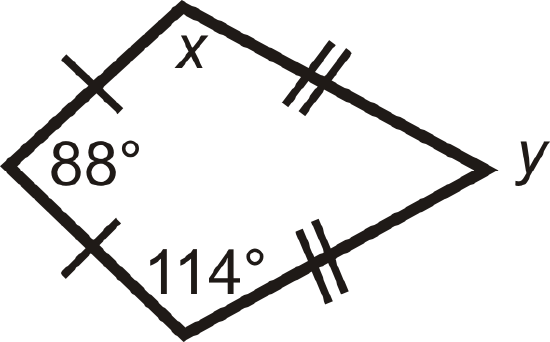
Figure \(\PageIndex{11}\) -
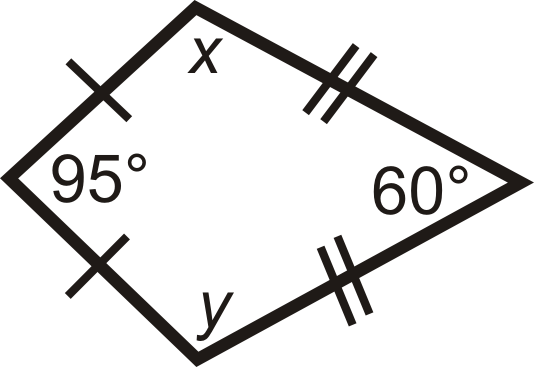
Figure \(\PageIndex{12}\) -
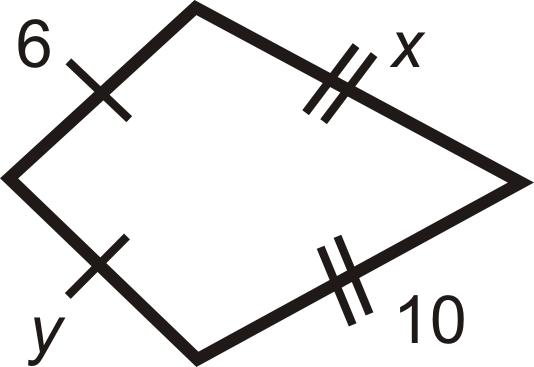
Figure \(\PageIndex{13}\) -
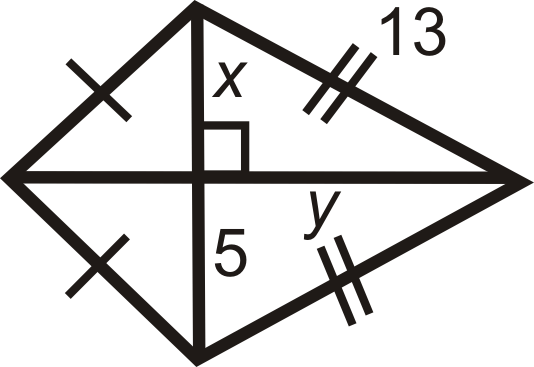
Figure \(\PageIndex{14}\) -
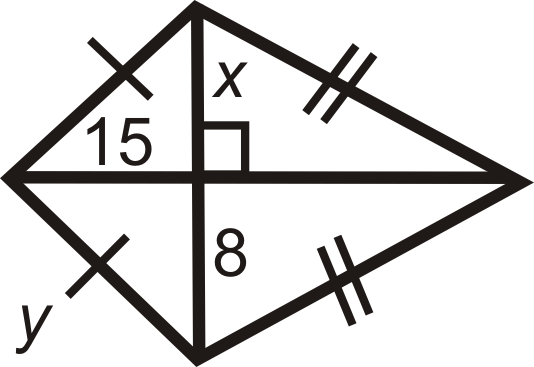 Figure \(\PageIndex{15}\)
Figure \(\PageIndex{15}\) -
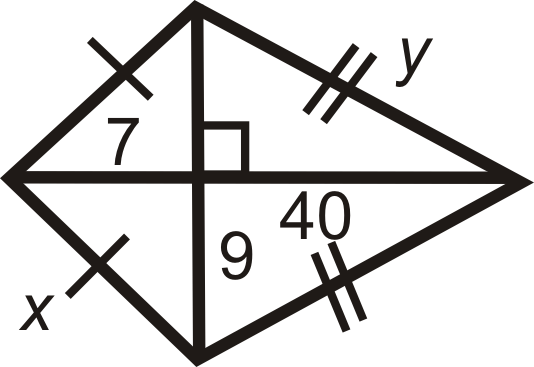
Figure \(\PageIndex{16}\)
For questions 7-11, find the value of the missing variable(s).
-
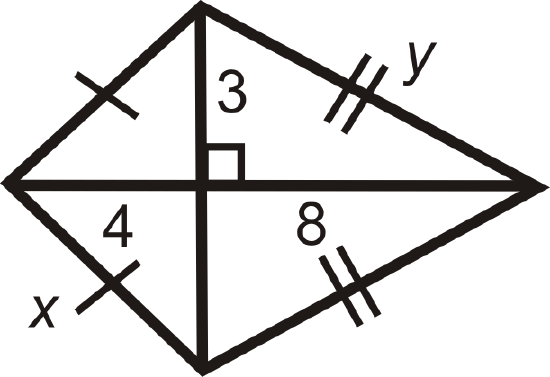
Figure \(\PageIndex{17}\) -
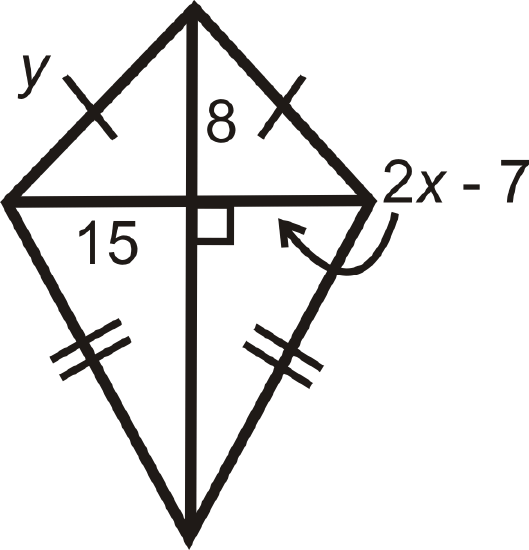
Figure \(\PageIndex{18}\) -
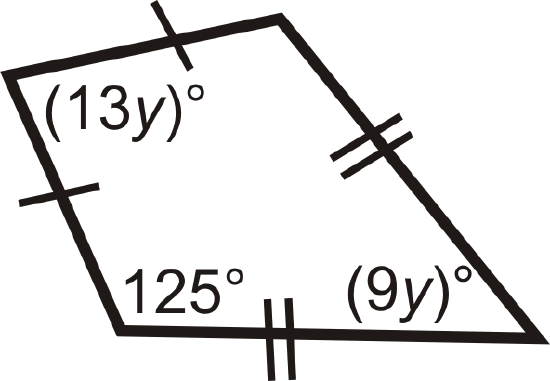
Figure \(\PageIndex{19}\) -
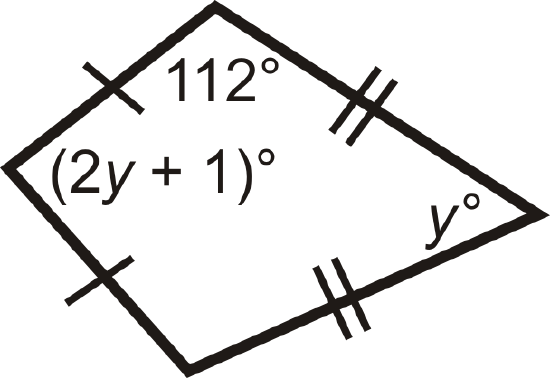
Figure \(\PageIndex{20}\) -
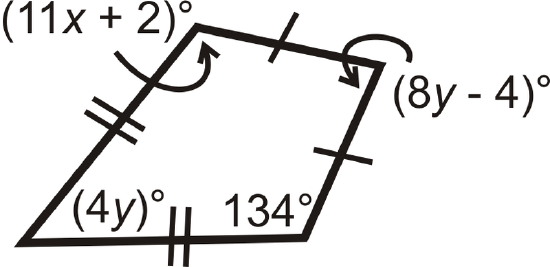
Figure \(\PageIndex{21}\)
- Fill in the blanks to the proof below.
Given: \(\overline{KE}\cong \overline{TE}\) and \(\overline{KI}\cong \overline{TI}\)
Prove: \(\overline{EI}\) is the angle bisector of \(\angle KET\) and \(\angle KIT\)

| Statement | Reason |
|---|---|
| 1.\( \overline{KE}\cong \overline{TE} and \overline{KI}\cong \overline{TI}\) | 1. |
| 2. \(\overline{EI}\cong \overline{EI}\) | 2. |
| 3. \(\Delta EKI\cong \Delta ETI\) | 3. |
| 4. | 4. CPCTC |
| 5. \(\overline{EI} is the angle bisector of \angle KET\) and \angle KIT\) | 5. |
- Fill in the blanks to the proof below.
Given: \(\overline{EK}\cong \overline{ET},\: \overline{KI}\cong \overline{IT}\)
Prove: \(\overline{KT}\perp \overline{EI}\)

| Statement | Reason |
|---|---|
| 1. \(\overline{KE}\cong \overline{TE}\) and \(\overline{KI}\cong \overline{TI}\) | 1. |
| 2. | 2. Definition of isosceles triangles |
| 3. \(\overline{EI}\) is the angle bisector of \(\angle KET\) and \(\angle KIT\) | 3. |
| 4. | 4. Isosceles Triangle Theorem |
| 5. \(\overline{KT}\perp \overline{EI}\) | 5. |
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.7.
Vocabulary
| Term | Definition |
|---|---|
| kite | A quadrilateral with distinct adjacent congruent sides. |
| Triangle Sum Theorem | The Triangle Sum Theorem states that the three interior angles of any triangle add up to 180 degrees. |
| Vertical Angles | Vertical angles are a pair of opposite angles created by intersecting lines. |
Additional Resources
Interactive Element
Video: Kites Principles - Basic
Activities: Kites Discussion Questions
Study Aids: Trapezoids and Kites Study Guide
Practice: Kites
Real World: Go Fly a Kite

