5.17: Area and Perimeter of Rhombuses and Kites
- Page ID
- 5001
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Area is half the product of the diagonals; perimeter is the sum of the sides.
Recall that a rhombus is a quadrilateral with four congruent sides and a kite is a quadrilateral with distinct adjacent congruent sides. Both of these quadrilaterals have perpendicular diagonals, which is how we are going to find their areas.
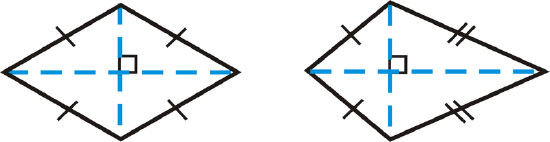
Notice that the diagonals divide each quadrilateral into 4 triangles. If we move the two triangles on the bottom of each quadrilateral so that they match up with the triangles above the horizontal diagonal, we would have two rectangles.
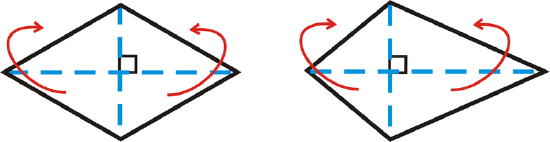
So, the height of these rectangles is half of one of the diagonals and the base is the length of the other diagonal.

The area of a rhombus or a kite is \(A=\dfrac{1}{2}d_1 d_2\)
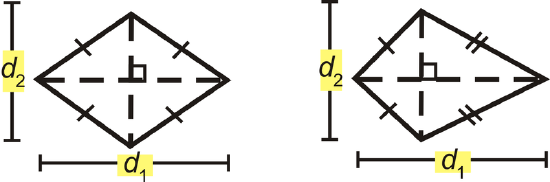
What if you were given a kite or a rhombus and the size of its two diagonals? How could you find the total distance around the kite or rhombus and the amount of space it takes up?
Example \(\PageIndex{1}\)
Find the perimeter and area of the kite below.
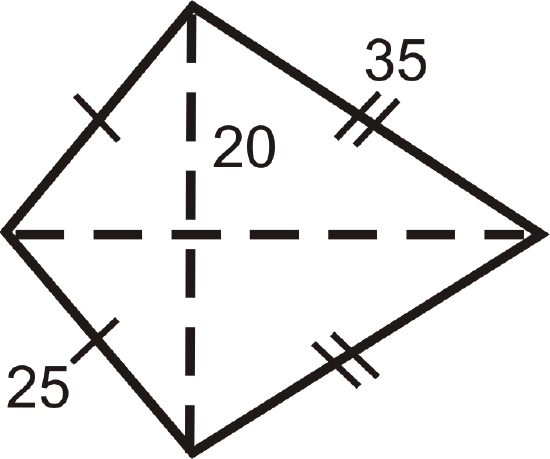
Solution
In a kite, there are two pairs of congruent triangles. Use the Pythagorean Theorem to find the lengths of sides or diagonals.
\(Smaller\: diagonal\: portion\)
\(20^2+d^2_s=25^2\)
\(d^2_s=225\)
\(d_s=15\: units\)
\(Larger\: diagonal\: portion\)
\(20^2+d^2_l=352 \)
\(d^2_l=825\)
\(d_l=5 units\)
\(A=\dfrac{1}{2}(15+5)(40)\cong 874.5 units^2\)
\(P=2(25)+2(35)=120\: units\)
Example \(\PageIndex{2}\)
Find the area of a rhombus with diagonals of 6 in and 8 in.
Solution
The area is \(\dfrac{1}{2}(8)(6)=24 in^2\).
Example \(\PageIndex{3}\)
Find the perimeter and area of the rhombus below.
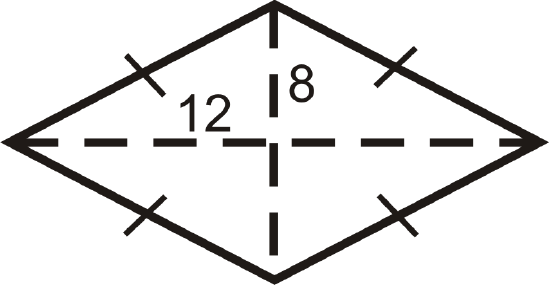
Solution
In a rhombus, all four triangles created by the diagonals are congruent.
To find the perimeter, you must find the length of each side, which would be the hypotenuse of one of the four triangles. Use the Pythagorean Theorem.
\(12^2+8^2=side^2\qquad A=12\cdot 16\cdot 24\)
\(144+64=side^2 \qquad A=192 units^2\)
\(side=\sqrt{208}\)
\(P=4\sqrt{13}=4(4\sqrt{13})=16\sqrt{13} units\)
Example \(\PageIndex{4}\)
Find the perimeter and area of the rhombus below.
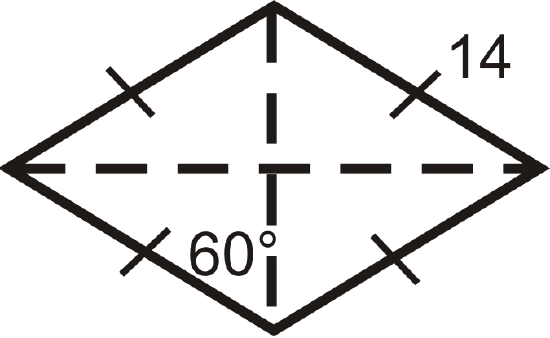
Solution
In a rhombus, all four triangles created by the diagonals are congruent.
Here, each triangle is a 30-60-90 triangle with a hypotenuse of 14. From the special right triangle ratios the short leg is 7 and the long leg is \(7\sqrt{3}\).
\(P=4\cdot 14=56 units \qquad A=12\cdot 14\cdot 14\sqrt{3}=98\sqrt{3} units^2\)
Example \(\PageIndex{5}\)
The vertices of a quadrilateral are \(A(2,8),B(7,9),C(11,2),\: and\: D(3,3)\). Show \(ABCD\) is a kite and find its area.
Solution
After plotting the points, it looks like a kite. \(AB=AD\) and \(BC=DC\). The diagonals are perpendicular if the slopes are negative reciprocals of each other.
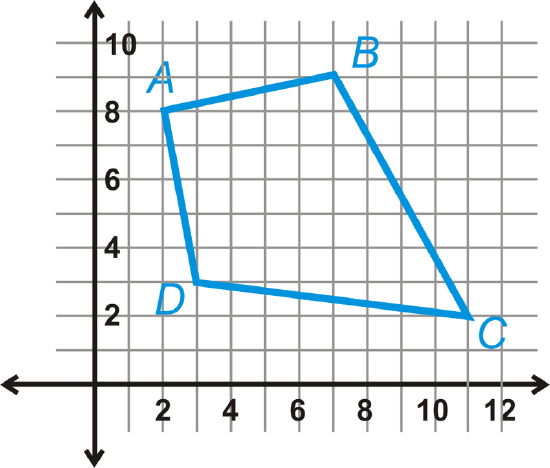
\(m_{AC}=\dfrac{2−8}{11−2}=−\dfrac{6}{9}=−\dfrac{2}{3}\)
\(m_{BD}=9−37−3=64=32\)
The diagonals are perpendicular, so \(ABCD\) is a kite. To find the area, we need to find the length of the diagonals, \(AC\) and \(BD\).
\(d_1=\sqrt{(2−11)^2+(8−2)^2}\)
\(=\sqrt{(−9)^2+6^2}\)
\(=\sqrt{81+36=\sqrt{117}=3\sqrt{13}\)
\(d_2=\sqrt{(7−3)^2+(9−3)^2}\)
\(=\sqrt{4^2+6^2}\)
\(=\sqrt{16+36}=\sqrt{52}=2\sqrt{13}\)
Plug these lengths into the area formula for a kite. \(A=12(3\sqrt{13})(2\sqrt{13})=39 units^2\)
Review
- Do you think all rhombi and kites with the same diagonal lengths have the same area? Explain your answer.
Find the area of the following shapes. Round your answers to the nearest hundredth.
-
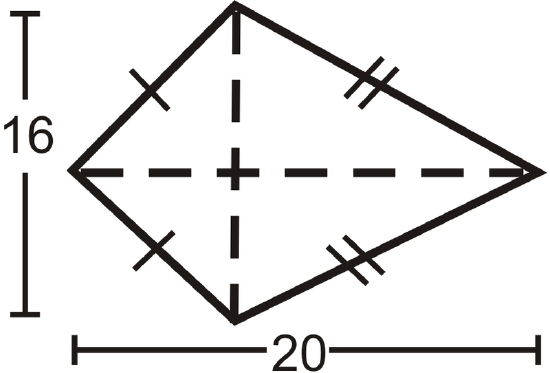
Figure \(\PageIndex{9}\) -
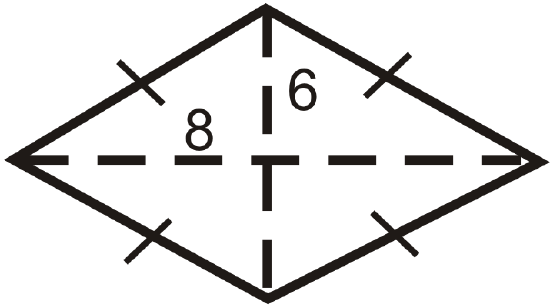
Figure \(\PageIndex{10}\) -
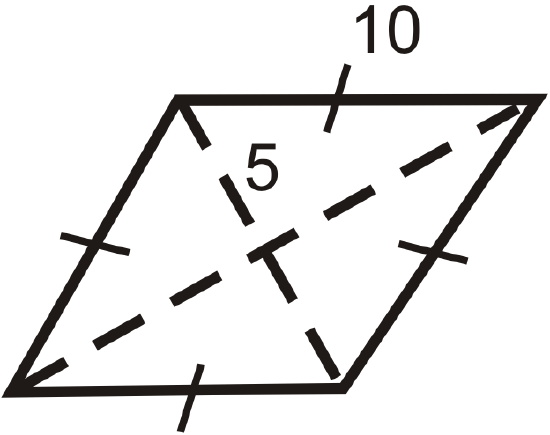
Figure \(\PageIndex{11}\) -
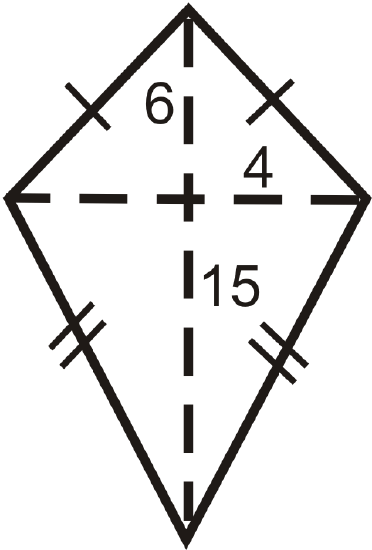
Figure \(\PageIndex{12}\) -
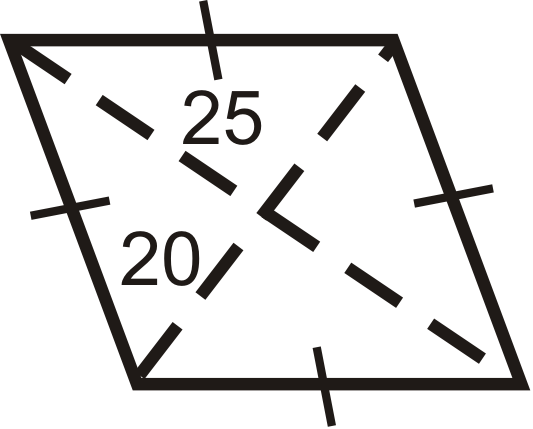
Figure \(\PageIndex{13}\) -
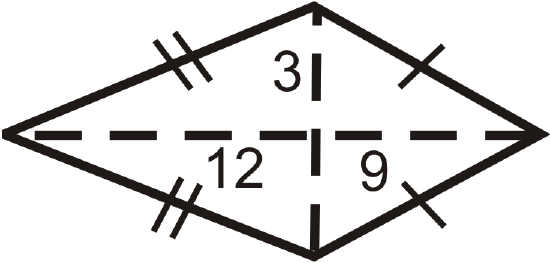
Figure \(\PageIndex{14}\)
Find the area and perimeter of the following shapes. Round your answers to the nearest hundredth.
-
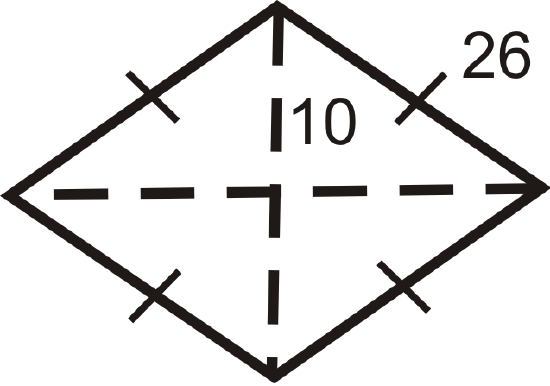
Figure \(\PageIndex{15}\) -
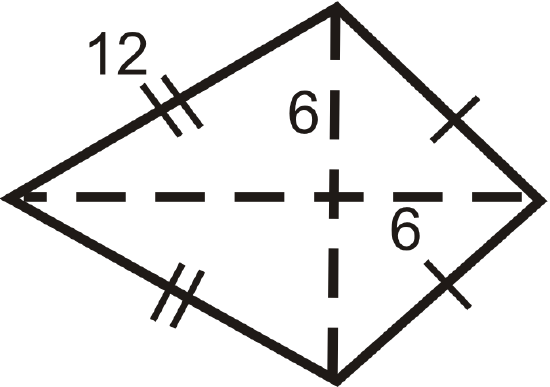
Figure \(\PageIndex{16}\) -
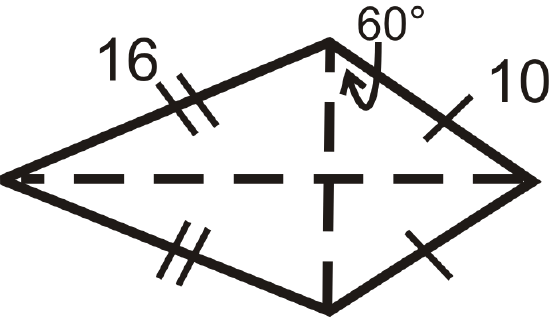
Figure \(\PageIndex{17}\) -
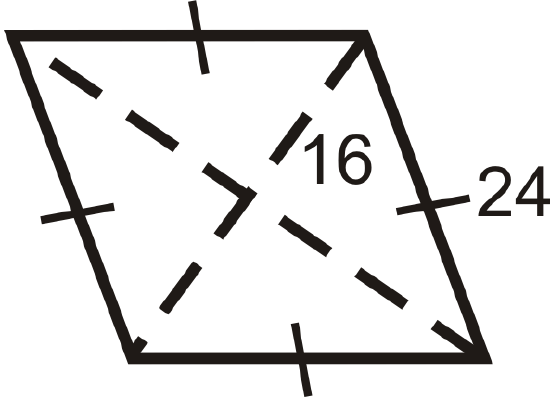
Figure \(\PageIndex{18}\)
For Questions 12 and 13, the area of a rhombus is \(32\: units^2\).
- What would the product of the diagonals have to be for the area to be \(32 units^2\)?
- List two possibilities for the length of the diagonals, based on your answer from #12.
For Questions 14 and 15, the area of a kite is \(54\: units^2\).
- What would the product of the diagonals have to be for the area to be \(54\: units^2\)?
- List two possibilities for the length of the diagonals, based on your answer from #14.
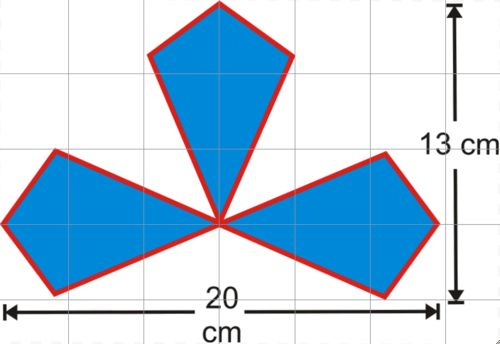
Sherry designed the logo for a new company, made up of 3 congruent kites.
- What are the lengths of the diagonals for one kite?
- Find the area of one kite.
- Find the area of the entire logo.
Vocabulary
| Term | Definition |
|---|---|
| area | The amount of space inside a figure. Area is measured in square units. |
| kite | A quadrilateral with distinct adjacent congruent sides. |
| perimeter | The distance around a shape. The perimeter of any figure must have a unit of measurement attached to it. If no specific units are given (feet, inches, centimeters, etc), write units. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Legs of a Right Triangle | The legs of a right triangle are the two shorter sides of the right triangle. Legs are adjacent to the right angle. |
Additional Resources
Interactive Element
Video: Area and Perimeter of Rhombuses and Kites Principles - Basic
Activities: Area and Perimeter of Rhombuses and Kites Discussion Questions
Study Aids: Triangles and Quadrilaterals Study Guide
Practice: Area and Perimeter of Rhombuses and Kites
Real World: Perimeter

