7.10: Proportional Triangles
- Page ID
- 5807
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sides divided by a line parallel to the third side of a triangle.
Triangle Proportionality Theorem
Think about a midsegment of a triangle. A midsegment is parallel to one side of a triangle and divides the other two sides into congruent halves. The midsegment divides those two sides proportionally. But what about another line that is parallel, but does not divide the other two sides into congruent halves? In fact, such a line will still divide the sides proportionally. This is called the Triangle Proportionality Theorem.
Triangle Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally.
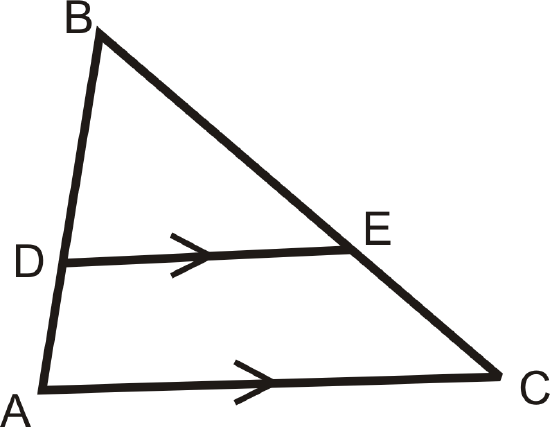
If \(\overline{DE}\parallel \overline{AC}\), then \(\dfrac{BD}{DA}=\dfrac{BE}{EC}\). (\(\dfrac{DA}{BD}=\dfrac{EC}{BE}\) is also a true proportion.)
The converse of this theorem is also true.
Triangle Proportionality Theorem Converse: If a line divides two sides of a triangle proportionally, then it is parallel to the third side.
If \(\dfrac{BD}{DA}=\dfrac{BE}{EC}\), then \(\overline{DE}\parallel \overline{AC}\).
What if you were given a triangle with a line segment drawn through it from one side to the other? How could you use information about the triangle's side lengths to determine if that line segment is parallel to the third side?
Use the diagram to answers Examples 1 and 2. \(\overline{DB}\parallel \overline{FE}\).
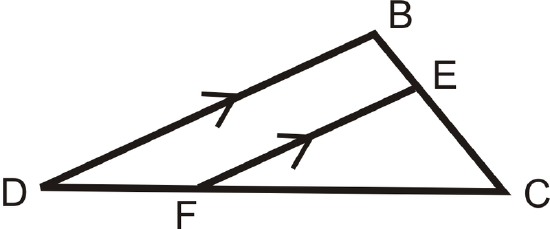
Example \(\PageIndex{1}\)
Name the similar triangles. Write the similarity statement.
Solution
\(\Delta DBC\sim \Delta FEC\)
Example \(\PageIndex{2}\)
\(\dfrac{FC+?}{FC}=\dfrac{?}{FE}\)
Solution
\(DF\); \(DB\)
Example \(\PageIndex{3}\)
A triangle with its midsegment is drawn below. What is the ratio that the midsegment divides the sides into?
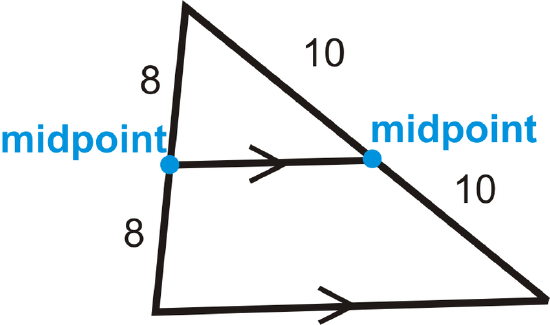
Solution
The midsegment splits the sides evenly. The ratio would be 8:8 or 10:10, which both reduce to 1:1.
Example \(\PageIndex{4}\)
In the diagram below, \(\overline{EB}\parallel \overline{CD}\). Find \(BC\).
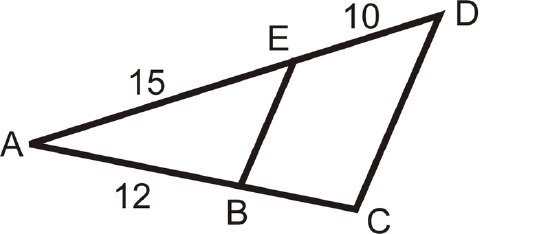
Solution
To solve, set up a proportion.
\(\begin{aligned} \dfrac{10}{15}=\dfrac{BC}{12} \rightarrow 15(BC)&=120 \\ BC&=8 \end{aligned}\)
Example \(\PageIndex{5}\)
Is \(\overline{DE}\parallel \overline{CB}\)?
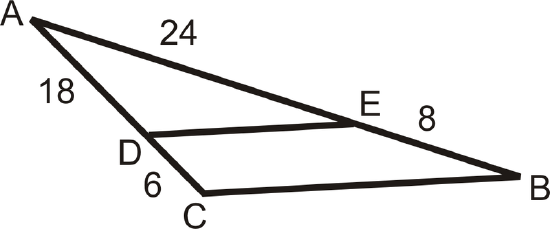
Solution
If the ratios are equal, then the lines are parallel.
\(\dfrac{6}{18}=\dfrac{8}{24}=\dfrac{1}{3}\)
Because the ratios are equal, \(\overline{DE}\parallel \overline{CB}\).
Review
Use the diagram to answer questions 1-7. \(\overline{AB}\parallel \overline{DE}\).
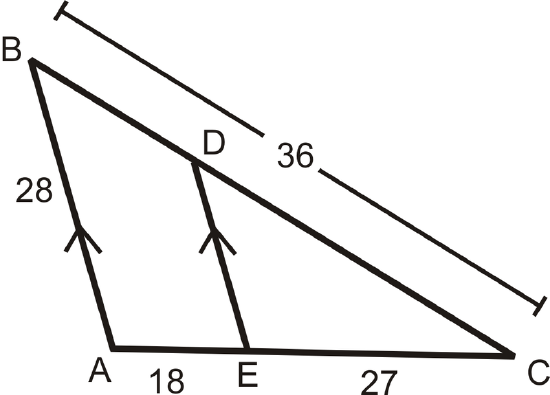
- Find \(BD\).
- Find \(DC\).
- Find \(DE\).
- Find \(AC\).
- What is \(BD:DC\)?
- What is \(DC:BC\)?
- Why \(BD:DC\neq DC:BC\)?
Use the given lengths to determine if \(\overline{AB}\parallel \overline{DE}\).
-
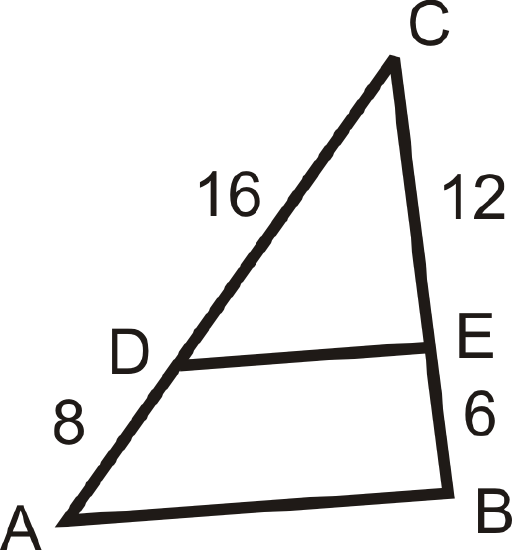
Figure \(\PageIndex{7}\) -
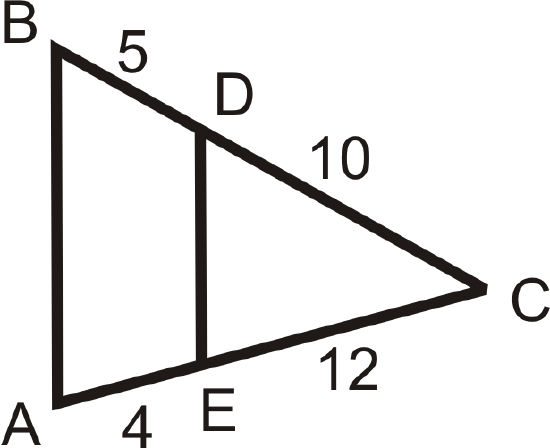
Figure \(\PageIndex{8}\) -

Figure \(\PageIndex{9}\) -
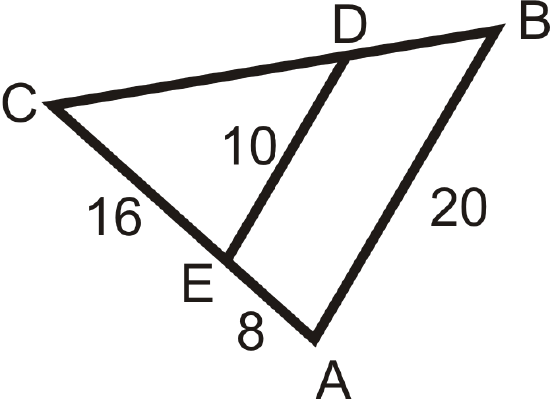
Figure \(\PageIndex{10}\) -
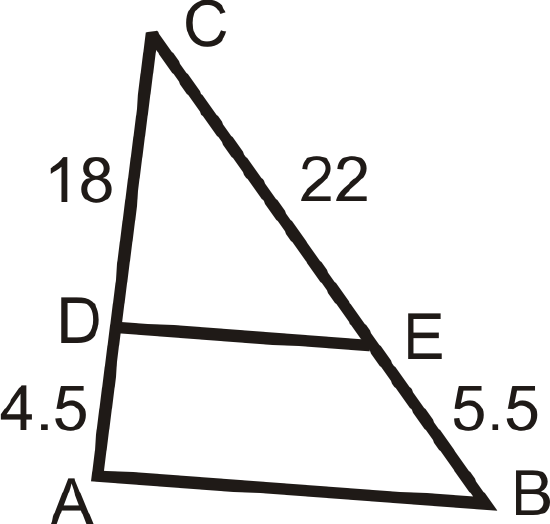
Figure \(\PageIndex{11}\) -
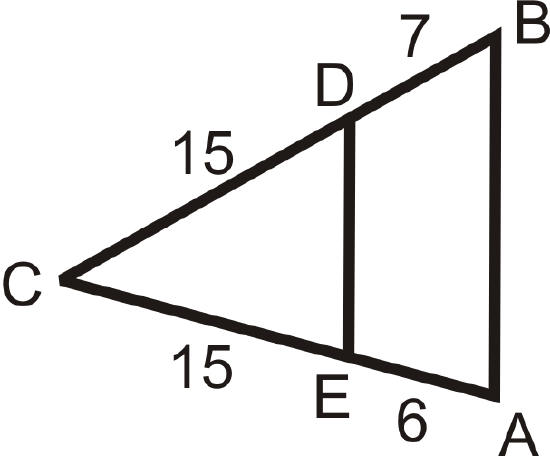
Figure \(\PageIndex{12}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 7.8.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Congruent | Congruent figures are identical in size, shape and measure. |
| midsegment | A midsegment connects the midpoints of two sides of a triangle or the non-parallel sides of a trapezoid. |
| Parallel | Two or more lines are parallel when they lie in the same plane and never intersect. These lines will always have the same slope. |
| Proportion | A proportion is an equation that shows two equivalent ratios. |
| Triangle Proportionality Theorem | The Triangle Proportionality Theorem states that if a line is parallel to one side of a triangle and it intersects the other two sides, then it divides those sides proportionally. |
| Triangle Proportionality Theorem Converse | The Triangle Proportionality Theorem converse states that if a line divides two sides of a triangle proportionally, then it is parallel to the third side. |
Additional Resources
Video: Using the Properties of the Triangle Proportionality Theorem to Solve for Unknown Values
Activities: Triangle Proportionality Discussion Questions
Study Aids: Proportionality Relationships Study Guide
Practice: Proportional Triangles
Real World: Triangle Proportionality

