7.11: Inscribed Similar Triangles
- Page ID
- 5815
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Division of a right triangle into similar triangles using an altitude.
Inscribed Similar Triangles Theorem
Remember that if two objects are similar, their corresponding angles are congruent and their sides are proportional in length. The altitude of a right triangle creates similar triangles.
Inscribed Similar Triangles Theorem: If an altitude is drawn from the right angle of any right triangle, then the two triangles formed are similar to the original triangle and all three triangles are similar to each other.
In \(\Delta ADB\), \(m\angle A=90^{\circ}\) and \(\overline{AC}\perp \overline{DB}\):
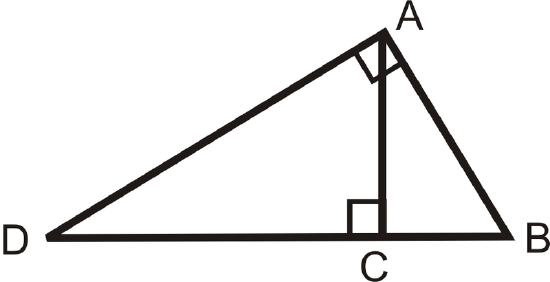
So, \(\Delta ADB\sim \Delta CDA\sim \Delta CAB\):

This means that all of the corresponding sides are proportional. You can use this fact to find missing lengths in right triangles.
What if you drew a line from the right angle of a right triangle perpendicular to the side that is opposite that angle? How could you determine the length of that line?
Example \(\PageIndex{1}\)
Find the value of \(x\).
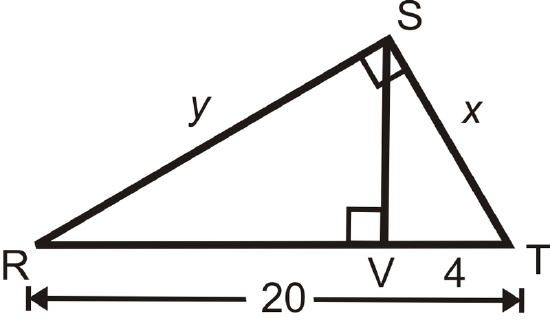
Solution
Set up a proportion.
\(\begin{aligned} \dfrac{\text{ shorter leg in }\Delta SVT}{\text{ shorter leg in }\Delta RST}&=\dfrac{\text{ hypotenuse in }\Delta SVT}{ \text{ hypotenuse in }\Delta RST} \\ \dfrac{4}{x}&=\dfrac{x}{20} \\ x^2&=80 \\ x&=\sqrt{80}=4\sqrt{5} \end{aligned}\)
Example \(\PageIndex{2}\)
Now find the value of \(y\) in \(\Delta RST\) above.
Solution
Use the Pythagorean Theorem.
\(\begin{aligned} y^2+(4\sqrt{5})^2&=20^2 \\y^2+80&=400 \\ y^2&=320 \\ y&=\sqrt{320}=8\sqrt{5}\end{aligned}\)
Example \(\PageIndex{3}\)
Find the value of \(x\).
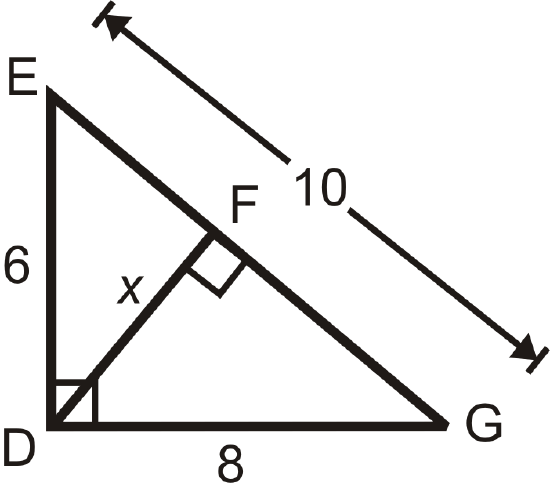
Solution
Separate the triangles to find the corresponding sides.
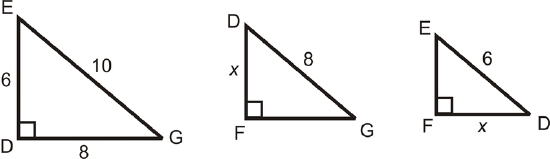
Set up a proportion.
\(\begin{aligned} \dfrac{\text{ shorter leg in } \Delta EDG}{\text{ shorter leg in } \Delta DFG}&=\dfrac{\text{ hypotenuse in }\Delta EDG}{\text{ hypotenuse in }\Delta DFG} \\ \dfrac{6}{x}&=\dfrac{10}{8} \\ 48&=10x \\ 4.8&=x \end{aligned}\)
Example \(\PageIndex{4}\)
Find the value of \(x\).
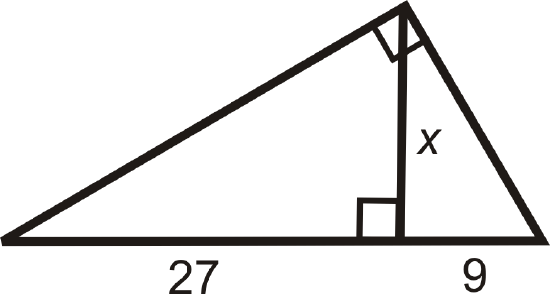
Solution
Set up a proportion.
\(\begin{aligned}\dfrac{\text{ shorter leg of smallest }\Delta}{\text{ shorter leg of middle } \Delta}=\dfrac{ \text{ longer leg of smallest }\Delta }{\text{ longer leg of middle }\Delta} \\ \dfrac{9}{x}&=\dfrac{x}{27} \\ x^2&=243 \\ x&=\sqrt{243}=9\sqrt{3}\end{aligned}\)
Example \(\PageIndex{5}\)
Find the values of \(x\) and \(y\).
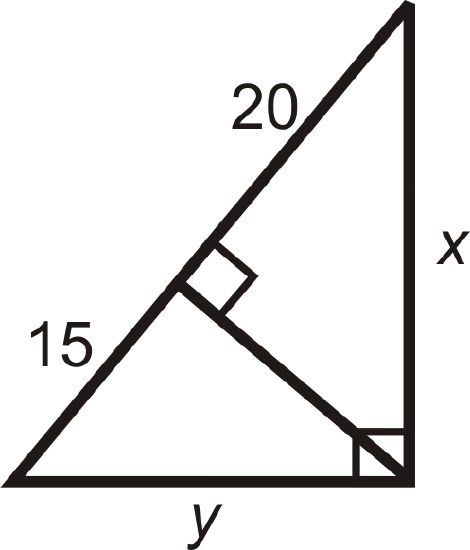
Separate the triangles. Write a proportion for \(x\).
Solution
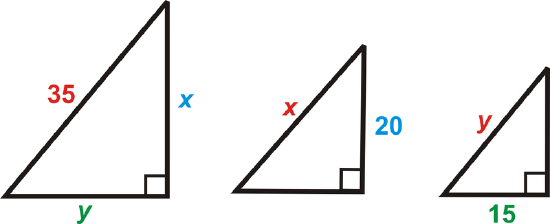
\(\begin{aligned} \dfrac{20}{x}&=\dfrac{x}{35} \\ x^2&=20\cdot 35 \\ x&=\sqrt{20\cdot 35} \\ x&=10\sqrt{7}\end{aligned}\)
Set up a proportion for y. Or, now that you know the value of x\) you can use the Pythagorean Theorem to solve for \(y\). Use the method you feel most comfortable with.
\(\begin{array}{rlrl}
\frac{15}{y} & =\frac{y}{35} & (10 \sqrt{7})^{2}+y^{2} & =35^{2} \\
y^{2} & =15 \cdot 35 & 700+y^{2}&=1225 \\
y & =\sqrt{15 \cdot 35} & y&=\sqrt{525}=5 \sqrt{21} \\& &
y &=5 \sqrt{21}
\end{array}\)
Review
Fill in the blanks.
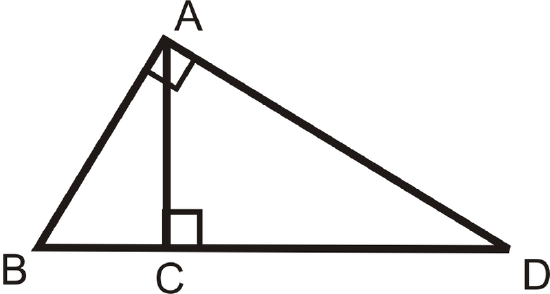
- \(\Delta BAD\sim \Delta ______ \sim \Delta ______\)
- \(\dfrac{BC}{?}=\dfrac{?}{CD}\)
- \(\dfrac{BC}{AB}=\dfrac{AB}{?}\)
- \(\dfrac{?}{AD}=\dfrac{AD}{BD}\)
Write the similarity statement for the right triangles in each diagram.
-
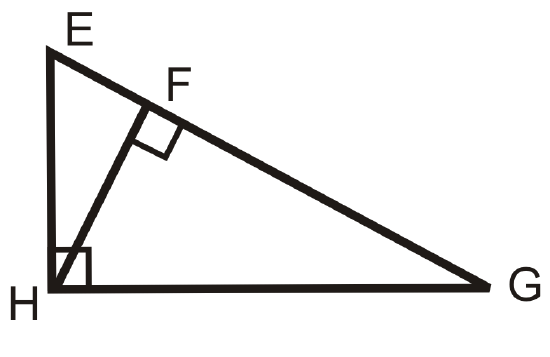
Figure \(\PageIndex{10}\) -
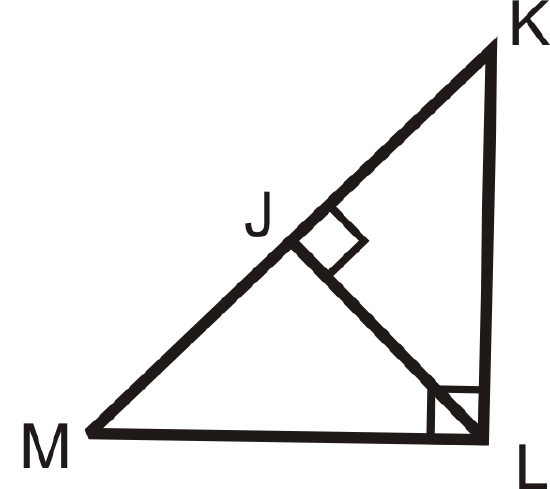
Figure \(\PageIndex{11}\)
Use the diagram to answer questions 7-10.
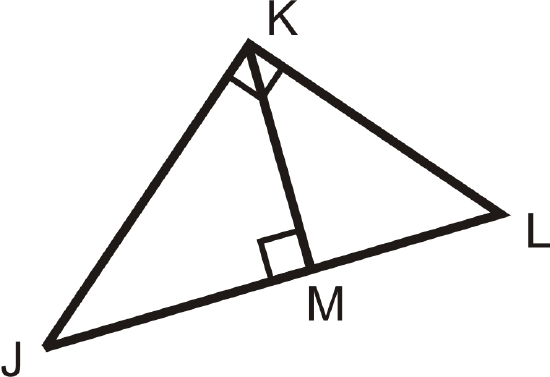
- Write the similarity statement for the three triangles in the diagram.
- If \(JM=12\) and \(ML=9\), find \(KM\).
- Find \(JK\).
- Find \(KL\).
Find the length of the missing variable(s). Simplify all radicals.
-
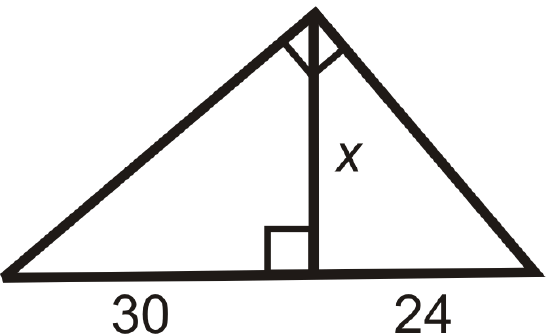
Figure \(\PageIndex{13}\) -
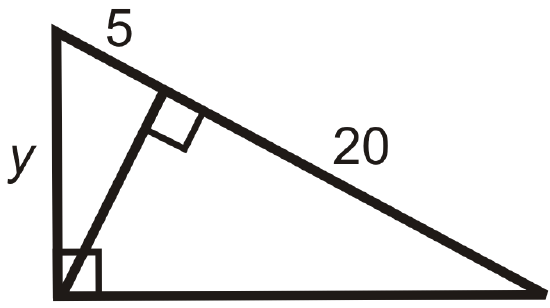
Figure \(\PageIndex{14}\) -
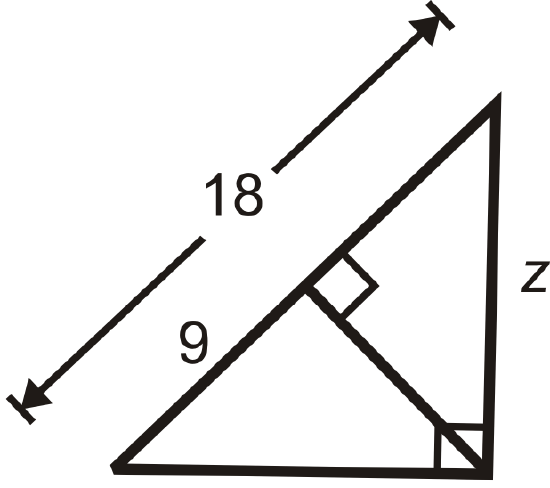
Figure \(\PageIndex{15}\) -
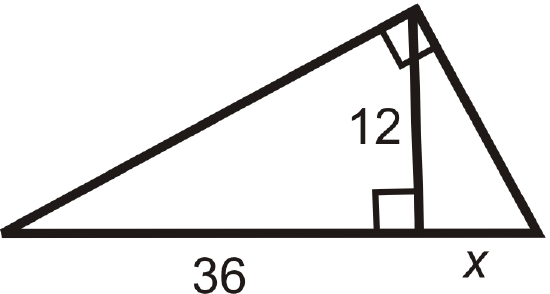
Figure \(\PageIndex{16}\) -
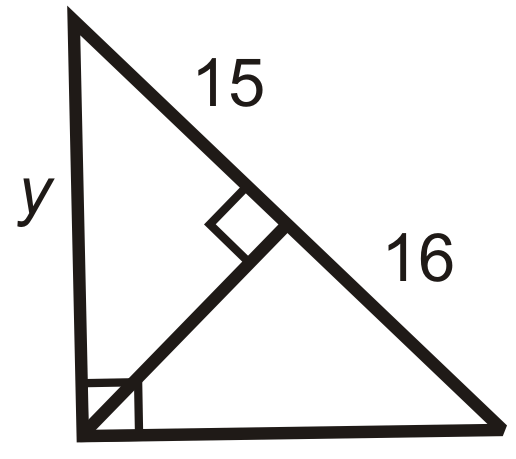
Figure \(\PageIndex{17}\) -
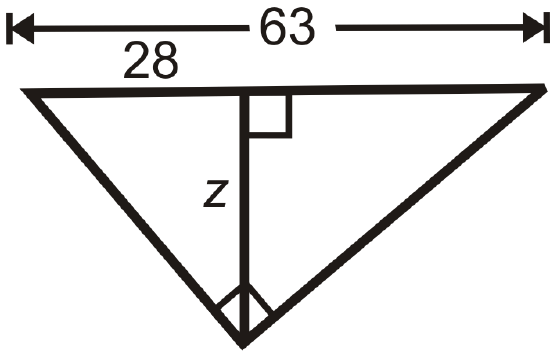
Figure \(\PageIndex{18}\) -
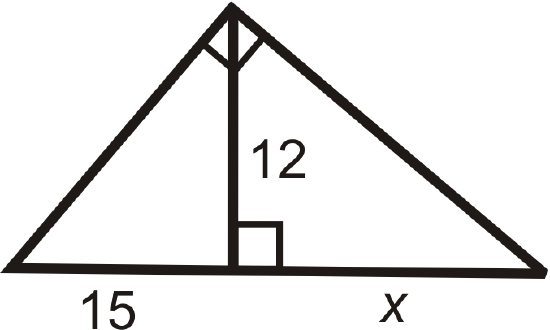
Figure \(\PageIndex{19}\) -
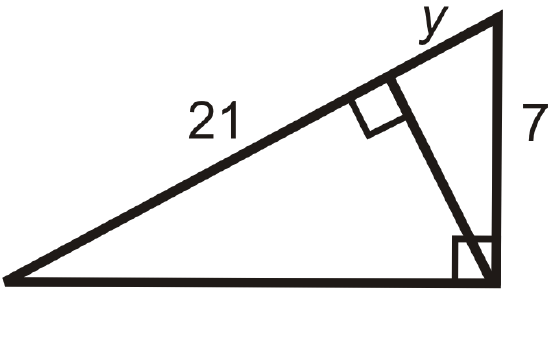
Figure \(\PageIndex{20}\) -
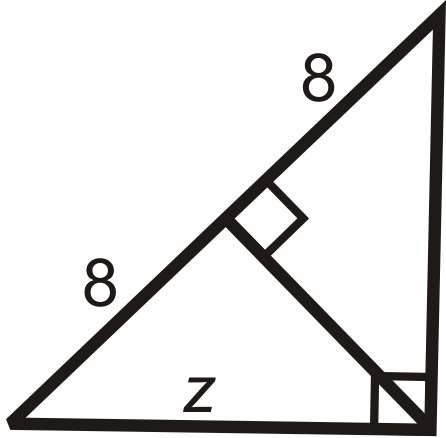
Figure \(\PageIndex{21}\) -
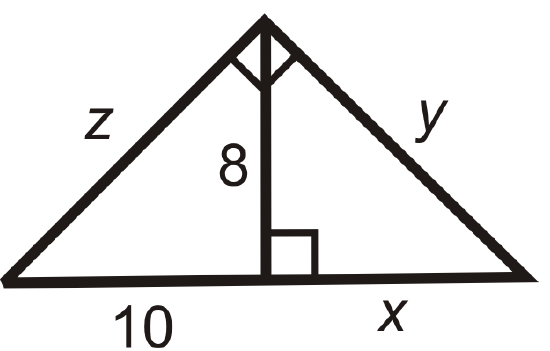
Figure \(\PageIndex{22}\) -
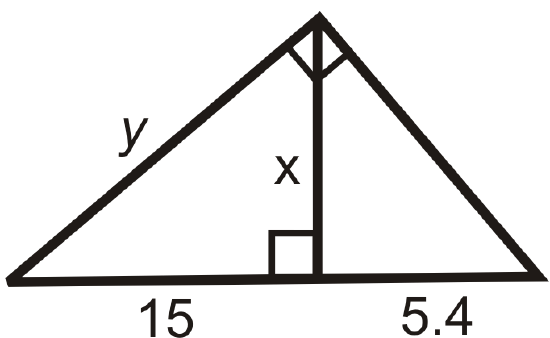
Figure \(\PageIndex{23}\) -
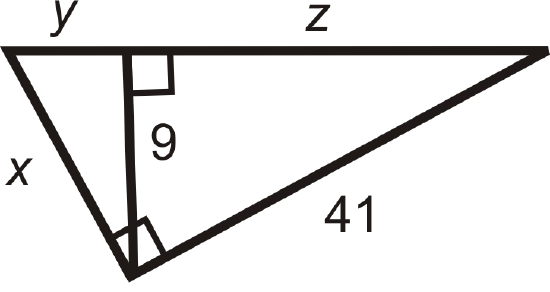
Figure \(\PageIndex{24}\) - Fill in the blanks of the proof for the Inscribed Similar Triangles Theorem.

Figure \(\PageIndex{25}\)
Given: \(\Delta ABD\) with \(\overline{AC}\perp \overline{DB}\) and \(\angle DAB\) is a right angle.
Prove: \(\Delta ABD\sim \Delta CBA\sim \Delta CAD\)
| Statement | Reason |
|---|---|
| 1. | 1. Given |
| 2. \(\angle DCA\) and \(\angle ACB\) are right angles | 2. |
| 3. \(\angle DAB\cong \angle DCA\cong \angle ACB\) | 3. |
| 4. | 4. Reflexive PoC |
| 5. | 5. AA Similarity Postulate |
| 6. \(B\cong \angle B\) | 6. |
| 7. \(\Delta CBA\cong \Delta ABD\) | 7. |
| 8. \(\Delta CAD\cong \Delta CBA\) | 8. |
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.4.
Vocabulary
| Term | Definition |
|---|---|
| Inscribed Similar Triangles Theorem | The Inscribed Similar Triangles Theorem states that if an altitude is drawn from the right angle of any right triangle, then the two triangles formed are similar to the original triangle and all three triangles are similar to each other. |
| Perpendicular | Perpendicular lines are lines that intersect at a 90∘ angle. The product of the slopes of two perpendicular lines is -1. |
| Proportion | A proportion is an equation that shows two equivalent ratios. |
| Pythagorean Theorem | The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle, given by \(a^2+b^2=c^2\), where a and b are legs of the triangle and c is the hypotenuse of the triangle. |
Additional Resources
Video: Inscribed Similar Triangles Principles - Basic
Activities: Inscribed Similar Triangles Discussion Questions
Study Aids: Right Triangle Similarity Study Guide
Practice: Inscribed Similar Triangles
Real World: Inscribed Similar Triangles

