7.12: Parallel Lines, Transversals, and Proportionality
- Page ID
- 5915
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As demonstrated by the the Triangle Proportionality Theorem, three or more parallel lines cut by two transversals divide them proportionally.
Triangle Proportionality Theorem
The Triangle Proportionality Theorem states that if a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally. We can extend this theorem to a situation outside of triangles where we have multiple parallel lines cut by transversals.
Theorem: If two or more parallel lines are cut by two transversals, then they divide the transversals proportionally.
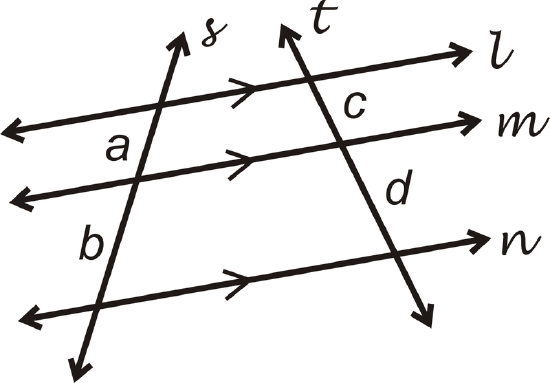Figure \(\PageIndex{1}\)If \(l\parallel m\parallel n\), then \(\dfrac{a}{b}=\dfrac{c}{d}\) or \(\dfrac{a}{c}=\dfrac{b}{d}\).
Note that this theorem works for any number of parallel lines with any number of transversals. When this happens, all corresponding segments of the transversals are proportional.
What if you were looking at a map that showed four parallel streets (A, B, C, and D) cut by two avenues, or transversals, (1 and 2)? How could you determine the distance you would have to travel down Avenue 2 to reach Street C from Street B given the distance down Avenue 1 from Street A to Street B, the distance down Avenue 1 from Street B to C, and the distance down Avenue 2 from Street A to B?
Example \(\PageIndex{1}\)
Find \(a\), \(b\), and \(c\).
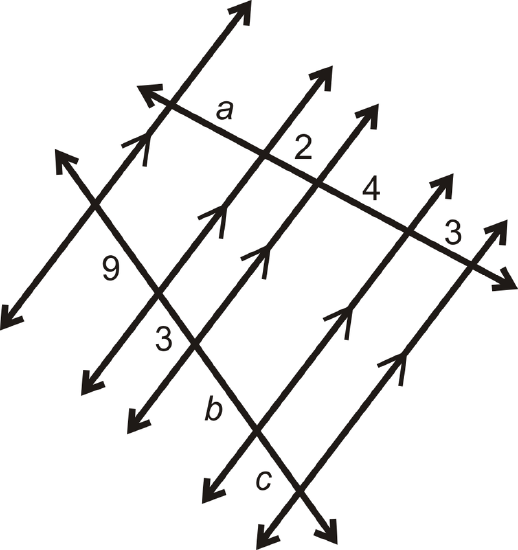
Solution
Line up the segments that are opposite each other.
\(\begin{array}{ccc}
\frac{a}{9}=\frac{2}{3} & \frac{2}{3}=\frac{4}{b} & \frac{2}{3}=\frac{3}{c} \\
3 a=18 & 2 b=12 & 2 c=9 \\
a=6 & b=6 & c=4.5
\end{array}\)
Example \(\PageIndex{1}\)
Below is a street map of part of Washington DC. R Street, Q Street, and O Street are parallel and 7th Street is perpendicular to all three. All the measurements are given on the map. What are x and y?
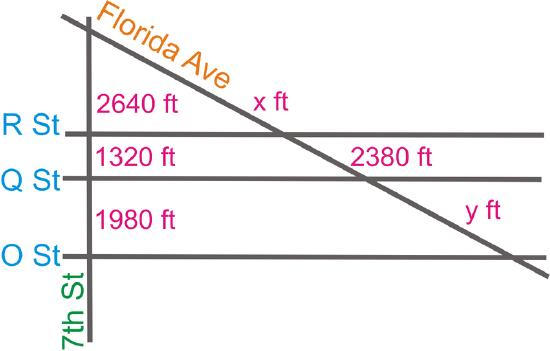
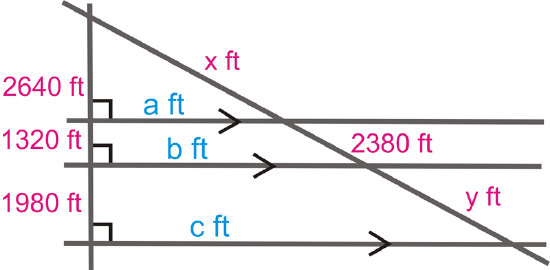
Solution
To find x and y, you need to set up a proportion using the parallel lines.
\(\dfrac{2640}{x}=\dfrac{1320}{2380}=\dfrac{1980}{y}\)
From this, \(x=4760\text{ ft }\) and \(y=3570\text{ ft }\).
Example \(\PageIndex{1}\)
Find \(a\).
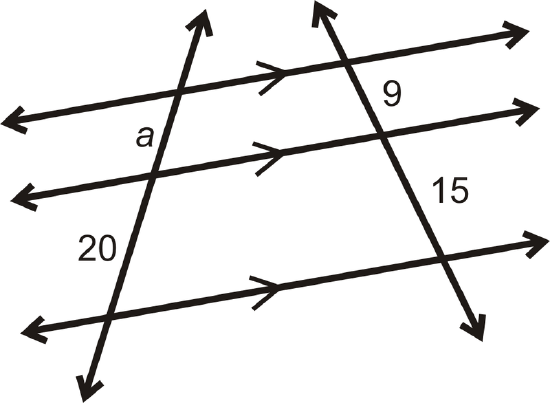
Solution
The three lines are marked parallel, so to solve, s et up a proportion.
\(\begin{aligned}\dfrac{a}{20}&=\dfrac{9}{15} \\ 180&=15a \\ a&=12 \end{aligned}\)
Example \(\PageIndex{1}\)
Find \(b\).
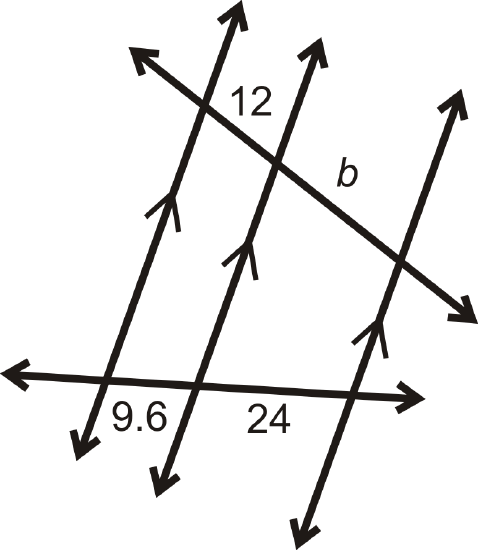
Solution
To solve, set up a proportion.
\(\begin{aligned} \dfrac{12}{9.6}&=\dfrac{b}{24} \\ 288&=9.6b \\ b&=30 \end{aligned}\)
Example \(\PageIndex{1}\)
Find the value of x\) that makes the lines parallel.
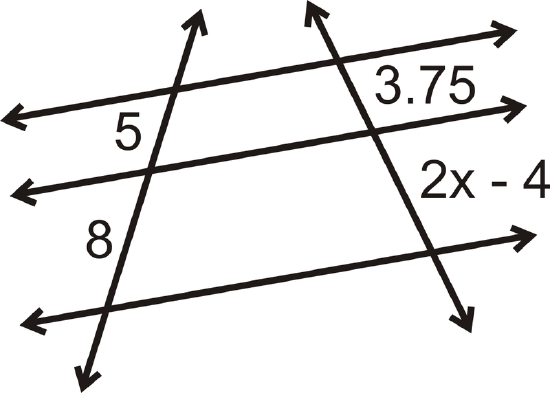
Solution
To solve, set up a proportion and solve for \(x\).
\(\begin{aligned}\dfrac{5}{8}&=\dfrac{3.75}{2x−4}\rightarrow 5(2x−4)&=8(3.75) \\ 10x−20&=30 \\ 10x&=50 \\ x&=5\end{aligned}\)
Review
Find the value of each variable in the pictures below.
-
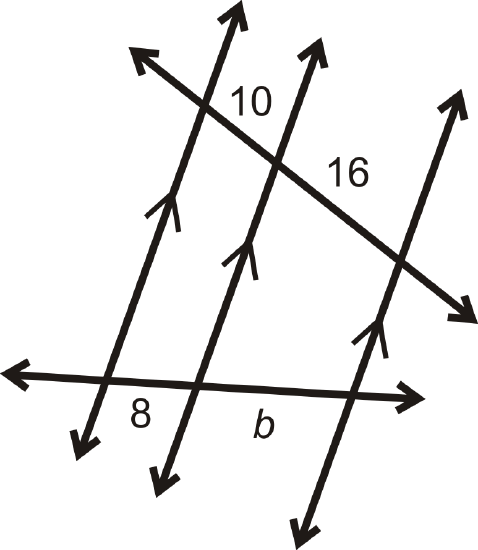
Figure \(\PageIndex{8}\) -
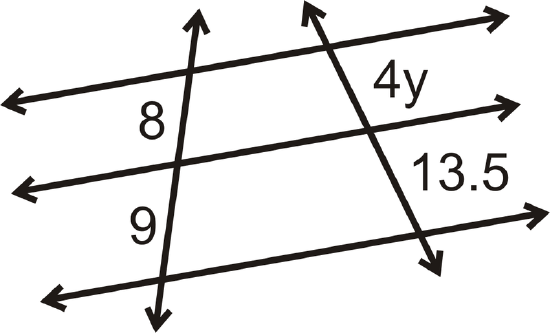
Figure \(\PageIndex{9}\) -
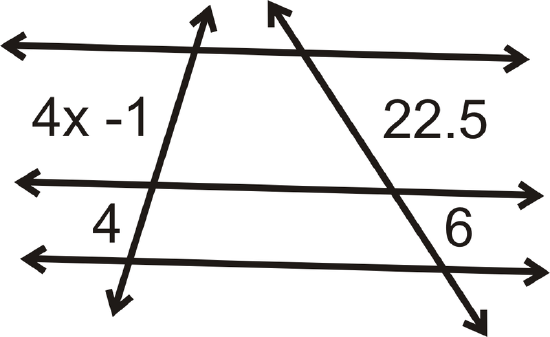
Figure \(\PageIndex{10}\) -
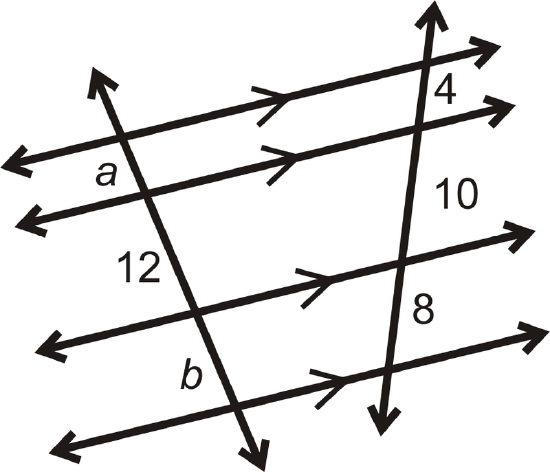
Figure \(\PageIndex{11}\) -
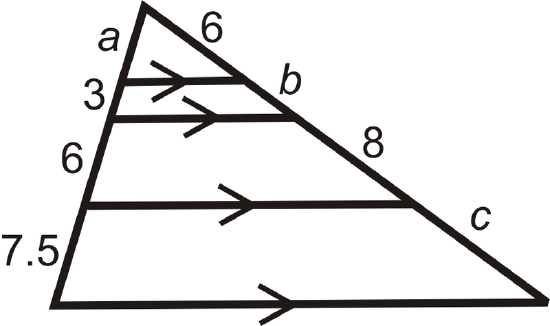
Figure \(\PageIndex{12}\)
The street map shows part of New Orleans. Burgundy St., Dauphine St. and Royal St. are parallel to each other. If Spain St. is perpendicular to all three, find the indicated distances.
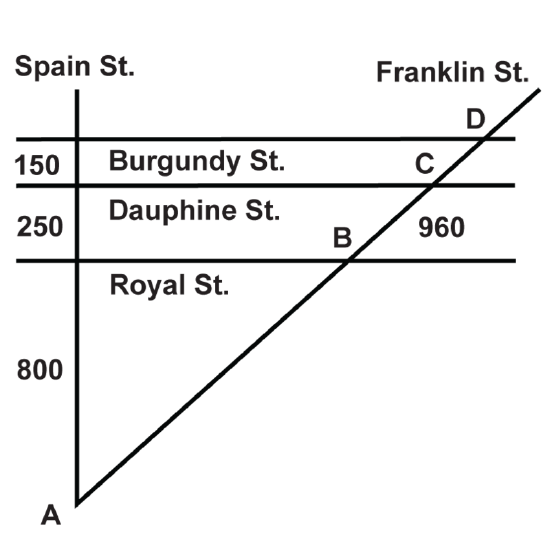
- What is the distance between points \(A\) and \(B\)?
- What is the distance between points \(C\) and \(D\)?
- What is the distance between points \(A\) and \(D\)?
Using the diagram, answer the questions.
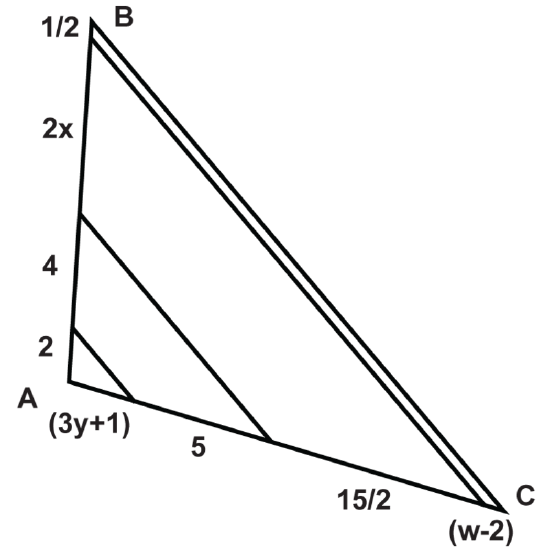
- What is the value of \(w\)?
- What is the value of \(x\)?
- What is the value of \(y\)?
- What is the length of \(\overline{AB}\)?
- What is the length of \(\overline{AC}\)?
Using the diagram, fill in the blank.
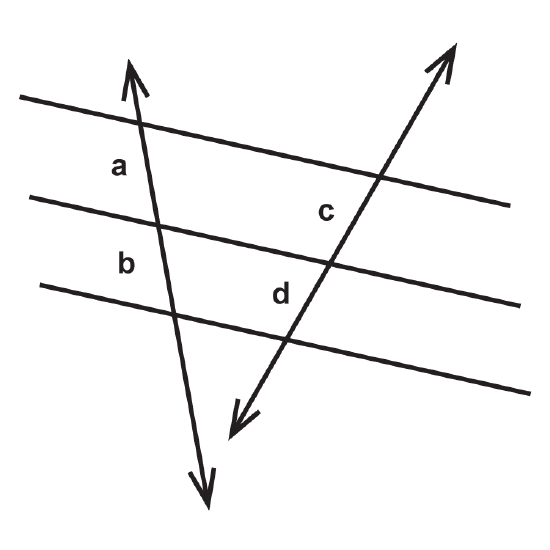
- If \(b\) is one-third \(d\), then \(a\) is ____________________.
- If \(c\) is two times \(a\), then \(b\) is ____________________.
Review (Answers)
To see the Review answers, open this PDF file and look for section 7.9.
Vocabulary
| Term | Definition |
|---|---|
| Coordinate Plane | The coordinate plane is a grid formed by a horizontal number line and a vertical number line that cross at the (0, 0) point, called the origin. The coordinate plane is also called a Cartesian Plane. |
| Perpendicular | Perpendicular lines are lines that intersect at a 90∘ angle. The product of the slopes of two perpendicular lines is -1. |
| Proportion | A proportion is an equation that shows two equivalent ratios. |
| Quadrilateral | A quadrilateral is a closed figure with four sides and four vertices. |
| transversal | A transversal is a line that intersects two other lines. |
| Triangle Proportionality Theorem | The Triangle Proportionality Theorem states that if a line is parallel to one side of a triangle and it intersects the other two sides, then it divides those sides proportionally. |
Additional Resources
Interactive Element
Video: Parallel Lines and Transversals Examples - Basic
Activities: Parallel Lines and Transversals Discussion Questions
Study Aids: Proportionality Relationships Study Guide
Practice: Parallel Lines, Transversals, and Proportionality
Real World: Parallel Lines And Transversals