7.9: SAS Similarity
- Page ID
- 5806
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Triangles are similar if two pairs of sides are proportional and the included angles are congruent.
SAS Similarity Theorem
By definition, two triangles are similar if all their corresponding angles are congruent and their corresponding sides are proportional. It is not necessary to check all angles and sides in order to tell if two triangles are similar. In fact, if you know only that two pairs of sides are proportional and their included angles are congruent, that is enough information to know that the triangles are similar. This is called the SAS Similarity Theorem.
SAS Similarity Theorem: If two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar.
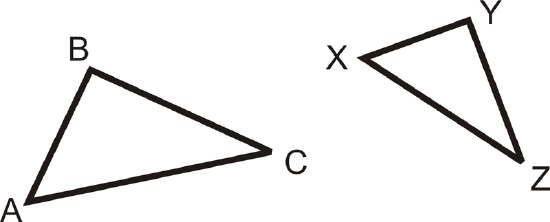
If \(\dfrac{AB}{XY}=\dfrac{AC}{XZ}\) and \(\angle A\cong \angle X\), then \(\Delta ABC\sim \Delta XYZ\).
What if you were given a pair of triangles, the lengths of two of their sides, and the measure of the angle between those two sides? How could you use this information to determine if the two triangles are similar?
Example \(\PageIndex{1}\)
Determine if the following triangles are similar. If so, write the similarity theorem and statement.
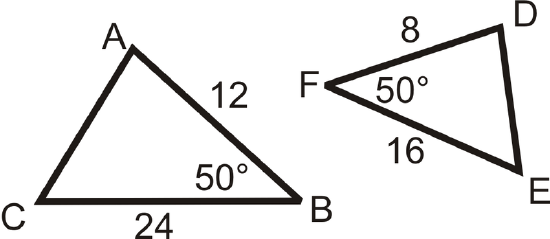
Solution
We can see that \(\angle B\cong \angle F\) and these are both included angles. We just have to check that the sides around the angles are proportional.
\(\begin{aligned} \dfrac{AB}{DF} &=\dfrac{12}{8}=\dfrac{3}{2} \\ \dfrac{BC}{FE}&=\dfrac{24}{16}=\dfrac{3}{2} \end{aligned}\)
Since the ratios are the same \(\Delta ABC\sim \Delta DFE\) by the SAS Similarity Theorem.
Example \(\PageIndex{2}\)
Determine if the following triangles are similar. If so, write the similarity theorem and statement.
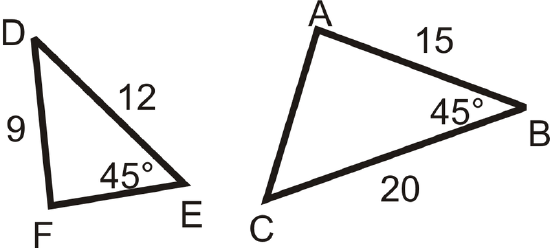
Solution
The triangles are not similar because the angle is not the included angle for both triangles.
Example \(\PageIndex{3}\)
Are the two triangles similar? How do you know?
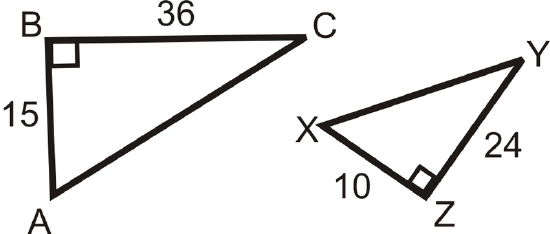
Solution
We know that \(\angle B\cong \angle Z\) because they are both right angles and \(\dfrac{10}{15}=\dfrac{24}{36}\). So, \(\dfrac{AB}{XZ}=\dfrac{BC}{ZY}\) and \(\Delta ABC\sim \Delta XZY\) by SAS.
Example \(\PageIndex{4}\)
Are there any similar triangles in the figure? How do you know?
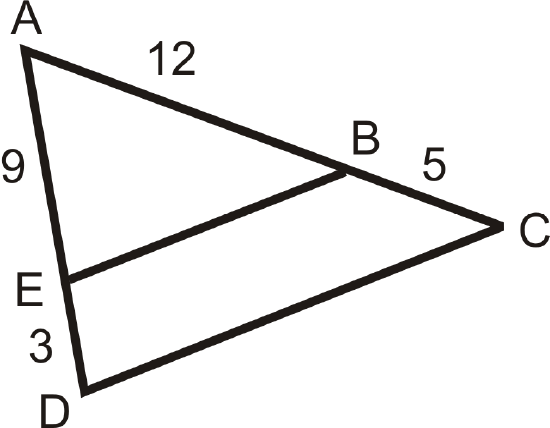
Solution
\(\angle A\) is shared by \(\Delta EAB\) and \(\Delta DAC\), so it is congruent to itself. Let’s see if \(\dfrac{AE}{AD}=\dfrac{AB}{AC}\).
\(\begin{aligned} \dfrac{9}{9+3}&=\dfrac{12}{12+5} \\ \dfrac{9}{12}&=\dfrac{3}{4}\neq \dfrac{12}{17}\qquad \text{ The two triangles are not similar. }\end{aligned}\)
Example \(\PageIndex{5}\)
From Example 4, what should \(BC\) equal for \(\Delta EAB\sim \Delta DAC\)?
Solution
The proportion we ended up with was \(\dfrac{9}{12}=\dfrac{3}{4}\neq \dfrac{12}{17}\). AC needs to equal 16, so that \(\dfrac{12}{16}=dfrac{3}{4}\). \(AC=AB+BC\) and \(16=12+BC\). \(BC\) should equal 4.
Review
Fill in the blanks.
- If two sides in one triangle are _________________ to two sides in another and the ________________ angles are _________________, then the triangles are ______________.
Determine if the following triangles are similar. If so, write the similarity theorem and statement.
-
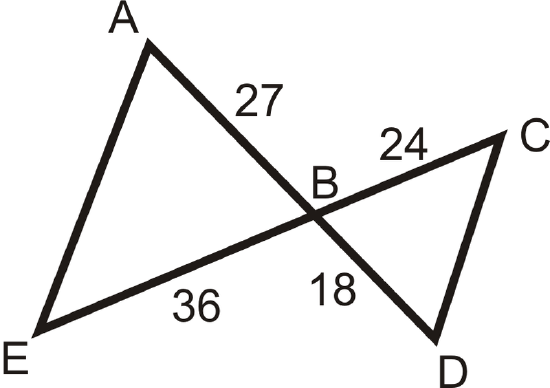
Figure \(\PageIndex{6}\)
Find the value of the missing variable(s) that makes the two triangles similar.
-
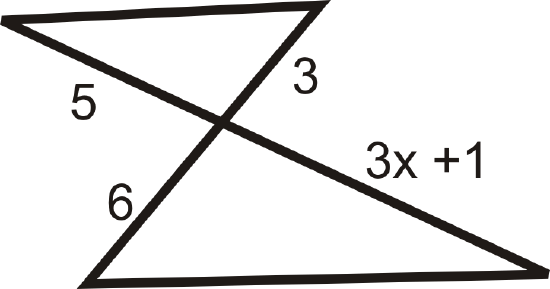
Figure \(\PageIndex{7}\) -
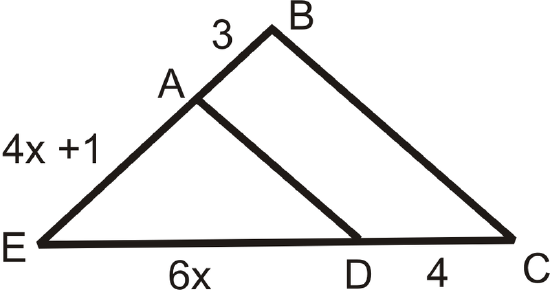
Figure \(\PageIndex{8}\) -
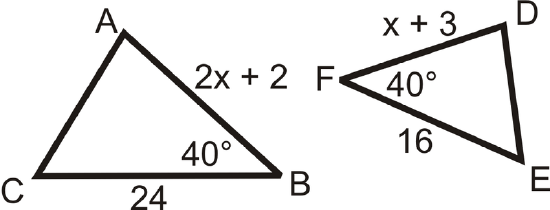
Figure \(\PageIndex{9}\)
Determine if the triangles are similar. If so, write the similarity theorem and statement.
- \(\Delta ABC\) is a right triangle with legs that measure 3 and 4. \(\Delta DEF\) is a right triangle with legs that measure 6 and 8.
- \(\Delta GHI\) is a right triangle with a leg that measures 12 and a hypotenuse that measures 13. \(\Delta JKL\) is a right triangle with legs that measure 1 and 2.
-
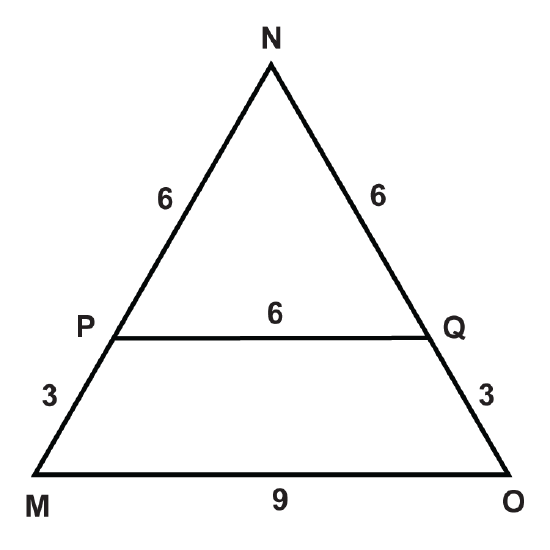
Figure \(\PageIndex{10}\) -
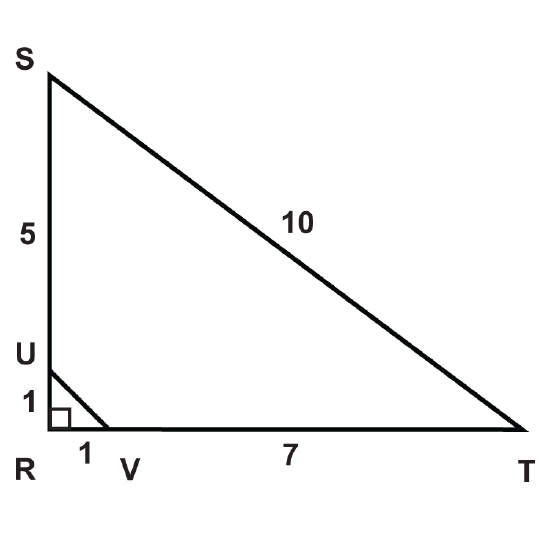
Figure \(\PageIndex{11}\) -
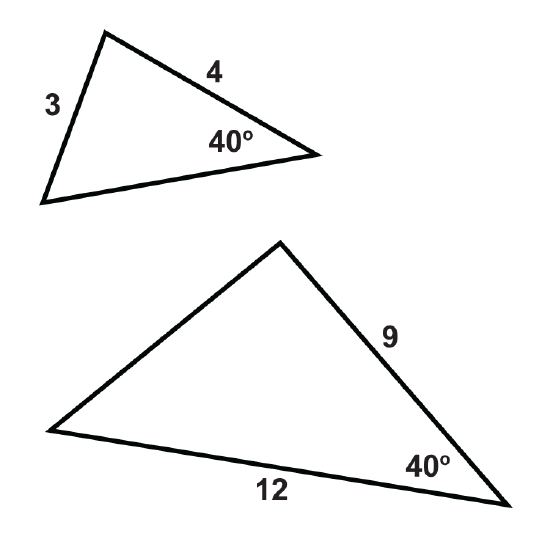
Figure \(\PageIndex{12}\) -
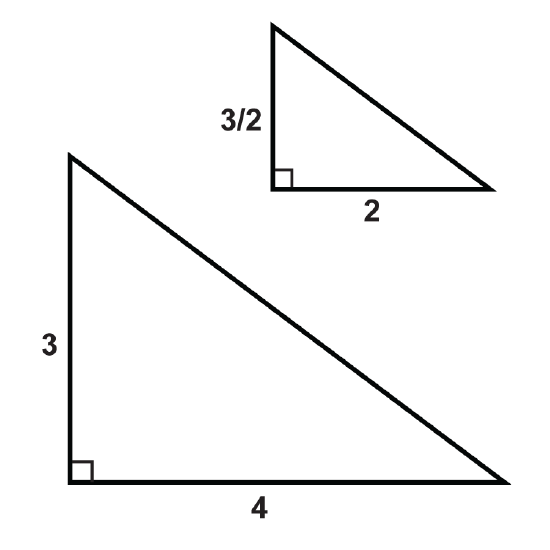
Figure \(\PageIndex{13}\) - \(\overline{AC}=3\)
\(\overline{DF}=6\)
-
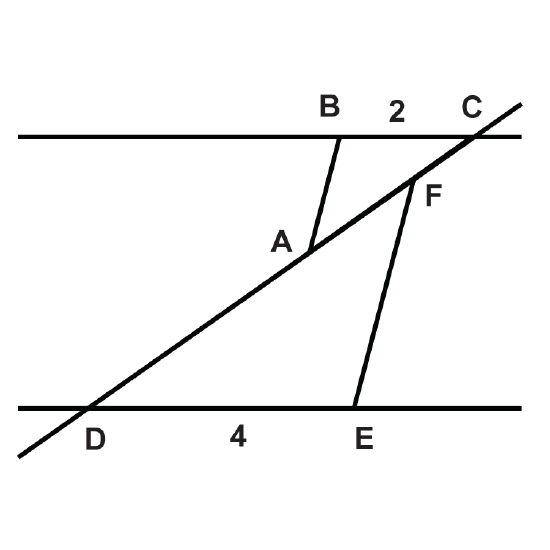
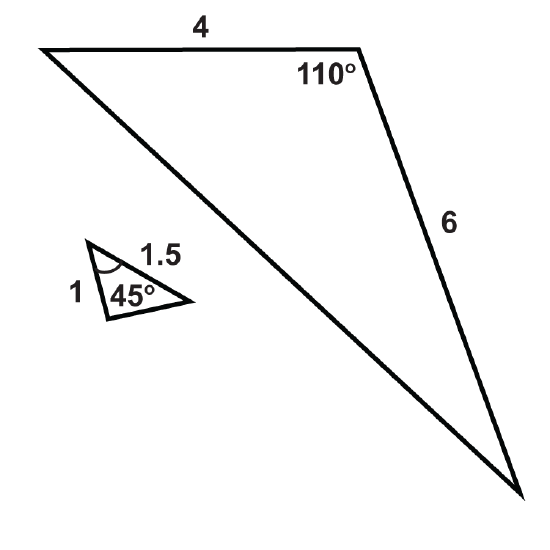
Figure \(\PageIndex{15}\) -
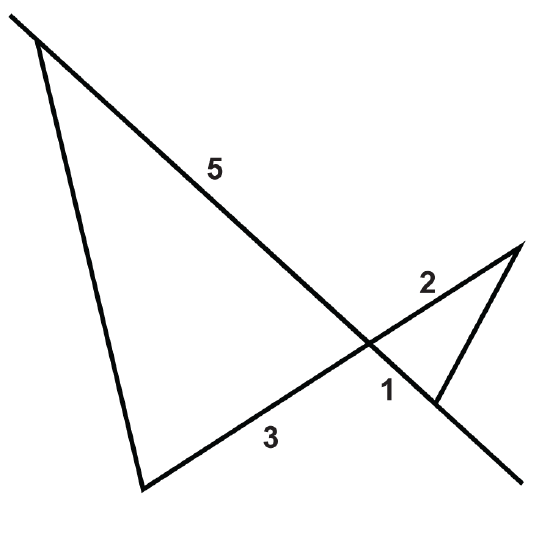
Figure \(\PageIndex{16}\) -
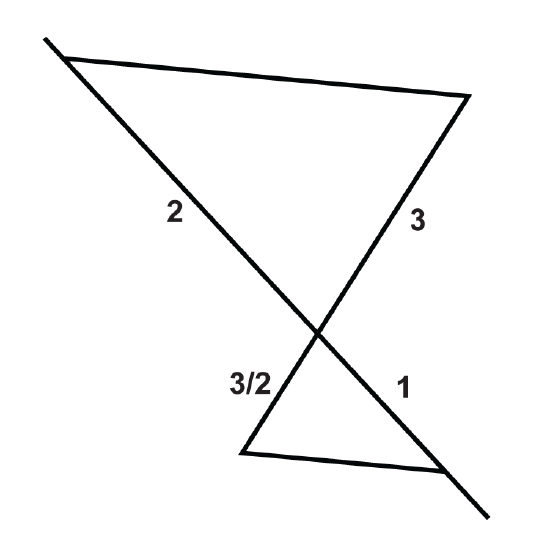
Figure \(\PageIndex{17}\
Review (Answers)
To see the Review answers, open this PDF file and look for section 7.7.
Resources
Vocabulary
| Term | Definition |
|---|---|
| AA Similarity Postulate | If two angles in one triangle are congruent to two angles in another triangle, then the two triangles are similar. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Dilation | To reduce or enlarge a figure according to a scale factor is a dilation. |
| SAS | SAS means side, angle, side, and refers to the fact that two sides and the included angle of a triangle are known. |
| SAS Similarity Theorem | The SAS Similarity Theorem states that if two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar. |
| Similarity Transformation | A similarity transformation is one or more rigid transformations followed by a dilation. |
Additional Resources
Interactive Element
Video: Congruent and Similar Triangles
Activities: SAS Similarity Discussion Questions
Study Aids: Polygon Similarity Study Guide
Practice: SAS Similarity
Real World: Triangle Similarity